Finding the Area of Oblique Triangles Using Heron's Formula | Grade 11 General Mathematics | Q3 W2
Summary
TLDRIn this tutorial, we learn how to find the area of oblique triangles using Heron's formula. An oblique triangle is one that doesn’t have a right angle and can either be acute or obtuse. Heron's formula allows us to calculate the area using only the side lengths of the triangle, without needing the height or angles. The video walks through two example problems, demonstrating the step-by-step process of applying Heron’s formula to compute the area of a triangular farm and a retention basin. Viewers are guided through calculating the semiperimeter and solving the formula to find the area.
Takeaways
- 😀 Oblique triangles do not have a right angle and can be either acute (all angles < 90°) or obtuse (one angle > 90°).
- 😀 A right triangle, in contrast, has one angle exactly equal to 90°.
- 😀 Heron's formula allows us to find the area of any triangle when all three sides are known, without needing to know any angles or height.
- 😀 The formula for Heron's area calculation is: A = √(s(s - a)(s - b)(s - c)), where 'a', 'b', and 'c' are the sides of the triangle, and 's' is the semiperimeter.
- 😀 The semiperimeter 's' is calculated as (a + b + c) / 2.
- 😀 Example 1: To find the area of a triangular farm with sides 12m, 9m, and 13m, the semiperimeter 's' is 17m, and the area is approximately 52.15 square meters.
- 😀 Example 2: For a retention basin with sides 20m, 15m, and 13m, the semiperimeter 's' is 24m, and the area is approximately 97.5 square meters.
- 😀 Heron's formula does not require knowledge of any angles, making it a straightforward method for finding triangle areas when only side lengths are known.
- 😀 The area calculated using Heron's formula is expressed in square units, based on the measurement of the sides (meters, feet, etc.).
- 😀 Understanding the difference between right, acute, and obtuse triangles is key to properly applying Heron's formula in various situations.
Q & A
What is an oblique triangle?
-An oblique triangle is a triangle that does not have a right angle. It can either be an acute triangle, where all angles are less than 90°, or an obtuse triangle, where one angle is greater than 90°.
How is an obtuse triangle different from an acute triangle?
-An obtuse triangle has one angle greater than 90° (e.g., 95°, 100°, 110°), whereas an acute triangle has all angles less than 90°.
What formula is used to find the area of a triangle when all three sides are known?
-The area of a triangle can be found using Heron's formula, which is: Area = √[s(s - a)(s - b)(s - c)], where 'a', 'b', and 'c' are the side lengths of the triangle, and 's' is the semi-perimeter, calculated as s = (a + b + c) / 2.
What is the semiperimeter of a triangle?
-The semiperimeter of a triangle is half of the perimeter. It is calculated as s = (a + b + c) / 2, where 'a', 'b', and 'c' are the lengths of the sides of the triangle.
In the example of Mang Lito’s farm, how is the semi-perimeter calculated?
-For Mang Lito's farm, the sides are 9 m, 12 m, and 13 m. The semi-perimeter is calculated as s = (9 + 12 + 13) / 2 = 34 / 2 = 17 m.
How do you apply Heron's formula to calculate the area of Mang Lito’s farm?
-Using Heron's formula, substitute the values s = 17, a = 9, b = 13, and c = 12 into the equation: Area = √[17(17 - 9)(17 - 13)(17 - 12)] = √[17 × 8 × 4 × 5] = √2720 ≈ 52.15 m².
What is the importance of the square root in Heron’s formula?
-The square root in Heron’s formula is necessary to calculate the actual area of the triangle from the product of the semi-perimeter and the differences (s - a), (s - b), and (s - c). It gives the final area in square units.
In the second example, how is the area of the barangay's retention basin calculated?
-For the retention basin, the sides are 20 m, 15 m, and 13 m. The semi-perimeter is calculated as s = (20 + 15 + 13) / 2 = 48 / 2 = 24 m. Then, using Heron’s formula: Area = √[24(24 - 20)(24 - 15)(24 - 13)] = √[24 × 4 × 9 × 11] = √9544 ≈ 97.5 m².
What unit of measurement is used when calculating the area using Heron's formula?
-The unit of measurement for the area is square meters (m²), since the side lengths are given in meters.
Is it necessary to know the height or angles of a triangle to use Heron's formula?
-No, Heron’s formula only requires the lengths of the three sides of the triangle. It does not require knowledge of the height or any angles.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
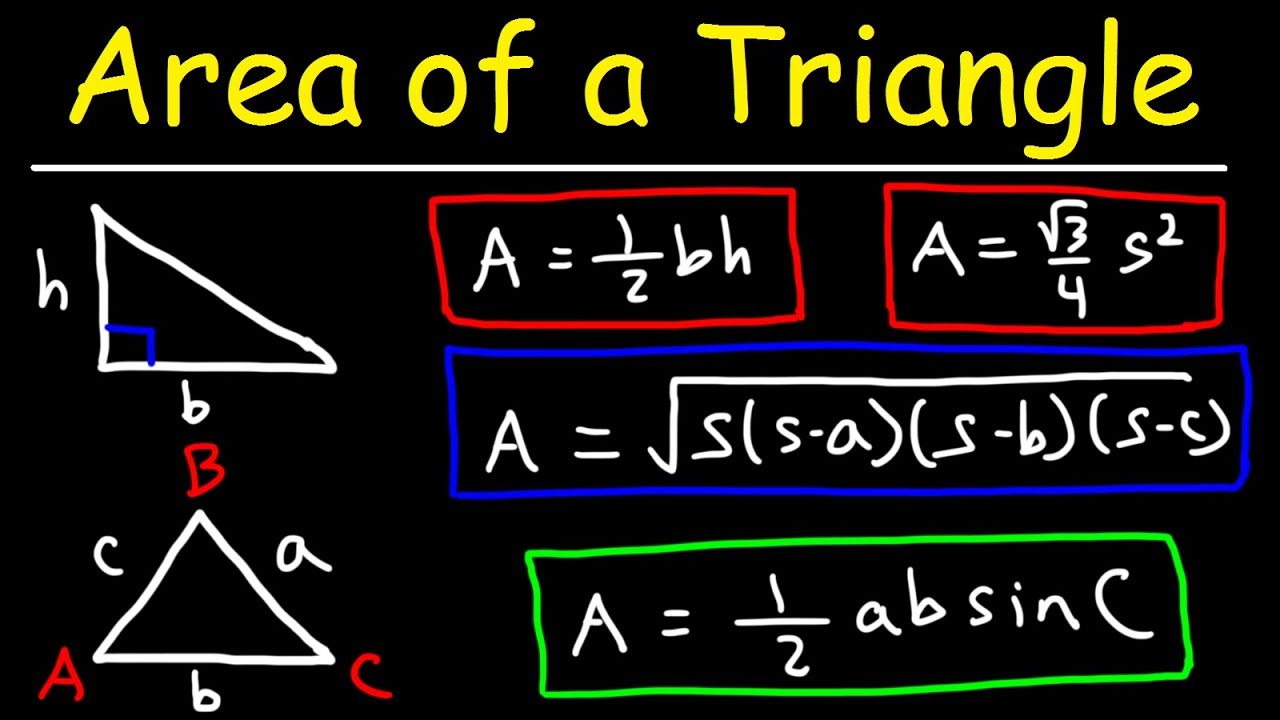
Area of a Triangle, Given 3 Sides, Heron's Formula

Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry

Module 4 Topic 5

Matematika SMA - Trigonometri (8) - Trigonometri Luas Segitiga, Rumus Luas Segitiga (A)

KELILING DAN LUAS SEGITIGA #MENEMUKAN RUMUS LUAS SEGITIGA#CONTOH SOAL#MATEMATIKA KELAS7
FÁCIL E RÁPIDO | ÁREA DO TRIÂNGULO - GEOMETRIA
5.0 / 5 (0 votes)
