Area of a Triangle, Given 3 Sides, Heron's Formula
Summary
TLDRThis video explores various methods for calculating the area of different types of triangles. It covers the basic area formula for right triangles using base and height, applies the Pythagorean theorem to find missing sides in isosceles triangles, and shows how to compute the area of equilateral triangles. The video also introduces Heron's formula for triangles with known side lengths and demonstrates how to find areas using trigonometry for side-angle-side scenarios. Through practical examples, viewers learn to tackle triangle area problems in diverse geometric situations.
Takeaways
- 😀 A right triangle's area can be calculated using the formula: 1/2 × base × height.
- 😀 For a right triangle with base 10 and height 12, the area is 60 square units (1/2 × 10 × 12 = 60).
- 😀 For any triangle, the area formula is 1/2 × base × height, regardless of the triangle's type.
- 😀 To calculate the area of an isosceles triangle, first split the triangle into two right triangles and use the Pythagorean theorem to find the height.
- 😀 In an isosceles triangle with a base of 8 and side lengths of 5, the height is found to be 3 using the Pythagorean theorem.
- 😀 An equilateral triangle's area can also be calculated using 1/2 × base × height, with the height calculated using the Pythagorean theorem or by using a specific formula for equilateral triangles.
- 😀 The area of an equilateral triangle with side length 10 can be found using the formula: √3/4 × s².
- 😀 The formula for the area of a triangle with two sides and an included angle (side-angle-side) is: 1/2 × side A × side B × sin(angle C).
- 😀 If the triangle is a right triangle, the formula simplifies to 1/2 × base × height, as sin(90°) equals 1.
- 😀 Heron's formula can be used to calculate the area of a triangle when all three sides are known. First, calculate the semi-perimeter (S), and then use the formula: √S(S-a)(S-b)(S-c), where a, b, and c are the triangle's sides.
Q & A
What is the basic formula for finding the area of a right triangle?
-The formula for the area of any triangle, including a right triangle, is 1/2 * base * height.
How do you calculate the area of a right triangle with a base of 10 and height of 12?
-Using the formula, the area is 1/2 * 10 * 12. First, divide 10 by 2 to get 5, then multiply by 12, giving an area of 60 square units.
What is the area of a triangle with a base of 8 and height of 6?
-Using the same area formula, 1/2 * 8 * 6 gives 24 square units.
How do you find the area of an isosceles triangle when the base is 8 units and the two congruent sides are 5 units each?
-To find the height, you can use the Pythagorean theorem. After finding the height, you can use the area formula 1/2 * base * height.
What is the Pythagorean theorem used for in triangle area calculation?
-The Pythagorean theorem helps find the height or missing side of a right triangle, which is often needed when calculating the area of triangles like isosceles triangles.
How do you find the height of an equilateral triangle when the side length is 10?
-For an equilateral triangle, split it in half to form two right triangles. Use the Pythagorean theorem to find the height, which will be approximately 5√3.
What is the formula for finding the area of an equilateral triangle, and how does it differ from other triangles?
-The formula for the area of an equilateral triangle is (√3 / 4) * s^2, where s is the side length. This formula is specific to equilateral triangles, unlike the general area formula (1/2 * base * height).
What is the area of an equilateral triangle with a side length of 10 using the formula (√3 / 4) * s^2?
-Using the formula, the area is (√3 / 4) * 10^2 = 25√3 square units.
How do you find the area of a triangle when you are given two sides and the included angle (side-angle-side method)?
-Use the formula Area = 1/2 * side A * side B * sin(C), where A and B are the sides, and C is the included angle.
What is Heron’s formula for calculating the area of a triangle with three sides known, and how is it applied?
-Heron’s formula is Area = √(s * (s - a) * (s - b) * (s - c)), where s is the semi-perimeter (half of the perimeter), and a, b, and c are the sides of the triangle.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Observasi Kelas Fokus Prilaku Penerapan Disiplin Positif di Kelas 5 SD Negeri 08 Selat Guntung

Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry

KELILING DAN LUAS SEGITIGA #MENEMUKAN RUMUS LUAS SEGITIGA#CONTOH SOAL#MATEMATIKA KELAS7
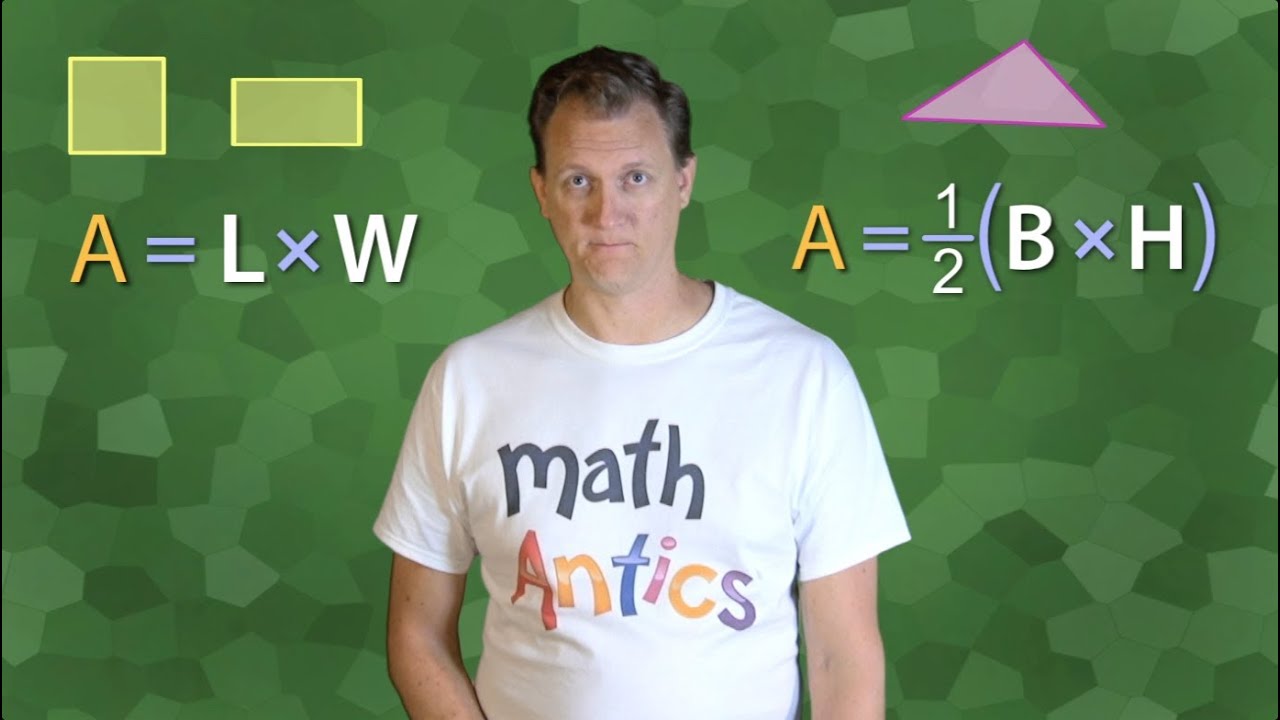
Math Antics - Area

Math 5 Quarter 1 Week 6 Revised K-12 Area Of A Parallelogram, Triangle, And Trapezoid

ÁREA DAS PRINCIPAIS FIGURAS PLANAS | GEOMETRIA PLANA
5.0 / 5 (0 votes)