Pembahasan Soal Statistika (ukuran pemusatan)
Summary
TLDRThe video script provides a detailed explanation of how to calculate the median of a dataset using class intervals and cumulative frequencies. The narrator walks through the process step-by-step, showing how to determine the median class, apply the median formula, and compute the result. The explanation emphasizes the importance of understanding frequency distributions and cumulative totals for solving problems related to the median, a common task in exams for universities and civil service tests. The script concludes with a simplified calculation example to reinforce the method.
Takeaways
- 😀 The script discusses how to find the median of a data set, specifically focusing on class intervals and cumulative frequencies.
- 😀 It explains that the median value of 163.5 cm corresponds to a specific class interval, and how to identify the median class.
- 😀 The script emphasizes the importance of understanding the formula for calculating the median, which involves the lower boundary of the median class, class interval length, and cumulative frequency.
- 😀 A detailed example is given, demonstrating how to calculate the median step-by-step with specific frequency values and class intervals.
- 😀 The calculation of cumulative frequencies is highlighted as essential for finding the correct median class.
- 😀 The script covers the necessary formula: Median = Lower boundary of the median class + (Class interval * ((n/2) - Cumulative frequency) / Frequency of median class).
- 😀 It stresses that the correct identification of the median class and accurate cumulative frequency is crucial for correct calculations.
- 😀 The example walks through the calculation of the cumulative frequency and how to apply it in finding the median class.
- 😀 The importance of understanding the relationship between the frequencies and the cumulative frequencies is also emphasized for accurate statistical analysis.
- 😀 Finally, the script concludes with a completed example showing how to compute the median value, ensuring the steps are clear for the viewer.
Q & A
What is the primary topic discussed in the transcript?
-The transcript primarily discusses how to calculate the median from a frequency distribution and provides a step-by-step guide for computing the median using the class interval and cumulative frequency.
What is the significance of the value 163.5 in the context of the script?
-The value 163.5 represents the median value of the data, which helps identify the class interval where the median lies. This is key to determining the median from a frequency distribution.
How is the median calculated from the data in the script?
-The median is calculated using the formula: Median = Lower boundary of the median class + [(N/2 - cumulative frequency before the median class) / frequency of the median class] * class width.
What role does the 'frequency cumulative' play in calculating the median?
-The cumulative frequency helps in identifying the class interval that contains the median. It is used to find out how many data points lie below or within each class, which is essential for determining the position of the median.
What does the formula in the script say about how the median is derived?
-The formula calculates the median by adjusting the lower boundary of the median class with the difference between the half total frequency (N/2) and the cumulative frequency before the median class, divided by the frequency of the median class. The result is then multiplied by the class width.
Why is it important to identify the median class?
-Identifying the median class is crucial because it is the class interval that contains the median value. Knowing this class allows the application of the median formula to accurately determine the median from the data.
What does the script mention about the use of formulas in solving problems?
-The script emphasizes that using formulas for median calculations makes the process more efficient, especially when dealing with frequency distributions. The formulas provide a clear structure for determining the median class and calculating the median accurately.
What does 'setengah n' refer to in the script?
-'Setengah n' refers to half of the total frequency (N/2), which is a critical part of the median calculation. It helps determine the position of the median within the data set.
What does the script suggest about handling tricky problems in statistical analysis?
-The script suggests that while formulas can seem complex, understanding how to apply them correctly to the given data set simplifies the process, even in challenging problems like those often seen in UT BK or other academic or professional tests.
How does the calculation process ensure an accurate median result?
-The calculation process ensures an accurate median result by considering the correct class interval, using the appropriate frequency and cumulative frequency values, and applying the formula systematically to account for the entire data distribution.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Contoh soal median data kelompok dan cara menghitung
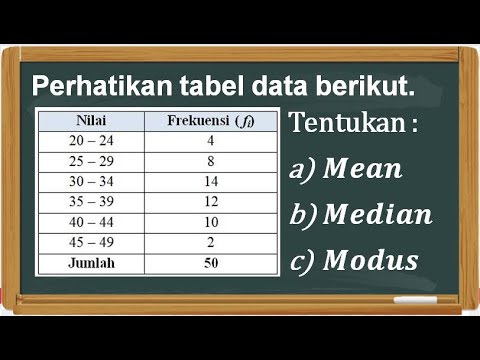
Menentukan Mean, Median, dan Modus Data Kelompok
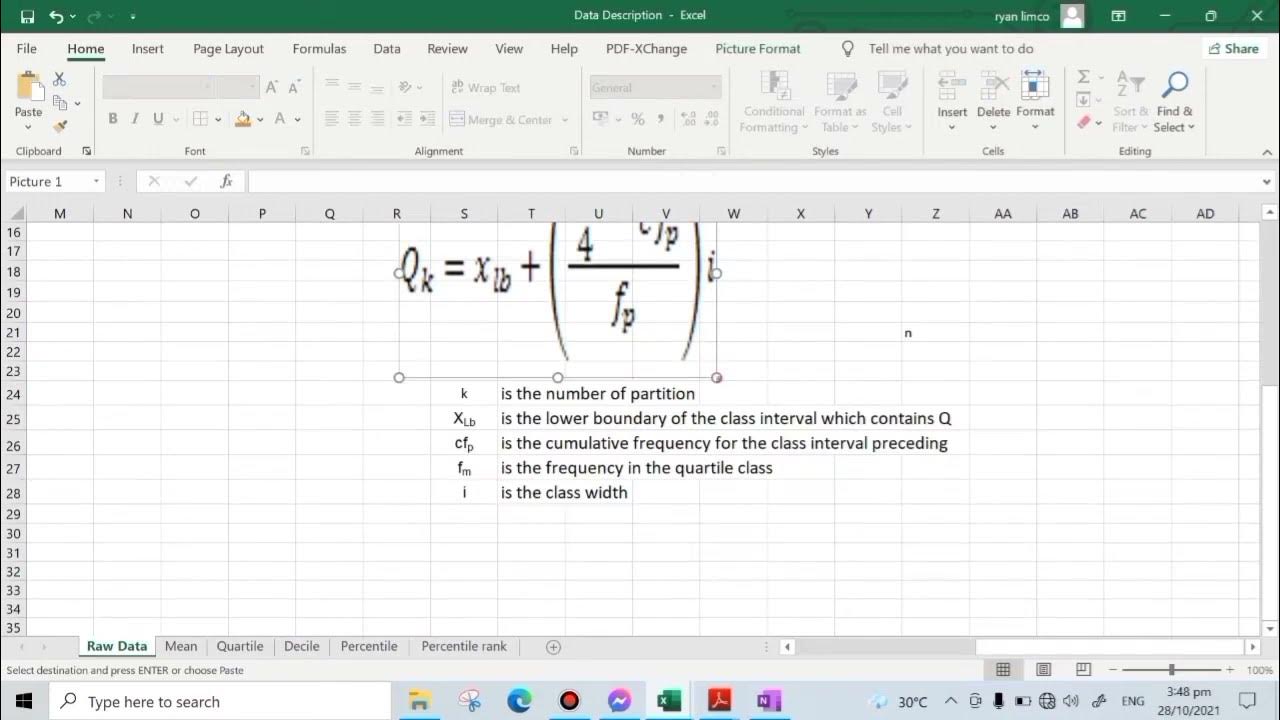
Grouped Mean, Quartile, Decile, Percentile, and Percentile Rank Using MS Excel. Statistics

Aprende a construir una Tabla de frecuencia con datos agrupados

Cumulative Frequency Diagrams - GCSE Higher Maths

Distribuição de frequência com classes
5.0 / 5 (0 votes)
