Contoh soal median data kelompok dan cara menghitung

Summary

This video explains how to calculate the median for grouped data using a step-by-step approach. It covers summing frequencies, identifying the median class, calculating the class width, and applying the median formula. By determining the cumulative frequency, lower boundary, and class width, the script demonstrates how to calculate the exact median value. The example uses a table with frequencies summing to 50, ultimately finding the median to be 12.17. This instructional content is ideal for those looking to understand statistical calculations for grouped data.

Takeaways

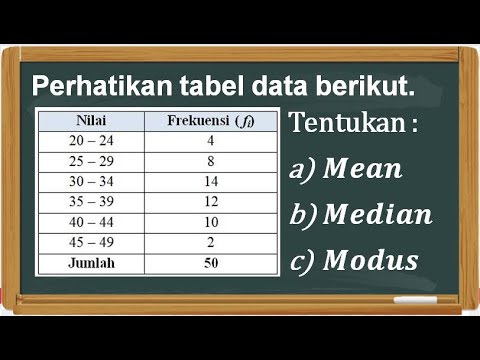
• 😀 The first step in calculating the median for grouped data is to sum the frequencies. In this case, the sum is 50.
• 😀 Next, calculate half of the total frequency (n), which in this case is 25 (half of 50).
• 😀 To find the median class, add frequencies from top to bottom until the cumulative frequency exceeds or equals 25.
• 😀 The median class is identified as the one where the cumulative frequency first exceeds or equals the value of 25.
• 😀 For this example, the median class starts at a cumulative frequency of 35, which exceeds 25, making it the correct class.
• 😀 The formula for determining the median class includes the frequency (fme) of the median class, which is 15 in this case.
• 😀 The next step is to determine the lower boundary (TB) of the median class, which is calculated as 10.5 (11 - 1/2).
• 😀 The class interval (c) is calculated by finding the difference between the upper and lower boundaries of the median class, which is 5.
• 😀 The cumulative frequency before the median class (Sigma fne) is 20, which is the sum of the frequencies before the median class.
• 😀 The median is calculated using the formula: Median = TB + (1/2n - Sigma fme) / fme * C. The result is approximately 12.17, which is the median value for the given data.

Q & A

What is the first step in calculating the median for grouped data?

The first step is to calculate the total frequency by summing up the individual frequencies. For the given example, the sum of frequencies is 50.

How do you calculate 1/2n in the median calculation process?

To calculate 1/2n, you multiply the total number of data points (n) by 1/2. In this case, since n = 50, 1/2 * 50 equals 25.

What is the purpose of determining the median class?

The median class is identified by finding the cumulative frequency that is greater than or equal to 25 (since 1/2n = 25), which helps in determining the class interval where the median lies.

How do you find the cumulative frequency for the median class?

You start adding the frequencies from top to bottom. Once the cumulative frequency reaches or exceeds 25, you identify the median class. In this case, after adding the frequencies, the cumulative frequency first exceeds 25 when you reach the class with a frequency of 15.

What does the term 'fme' represent in this calculation?

The term 'fme' refers to the frequency of the median class. In this case, fme equals 15, as it is the frequency of the class containing the median.

How is the lower boundary of the median class (TB) calculated?

The lower boundary (TB) of the median class is calculated by subtracting 1/2 from the lower boundary of the median class interval. For the median class 11-15, the lower boundary is 11, and TB is calculated as 11 - 1/2, which equals 10.5.

What is the significance of the 'c' value in the median formula?

The 'c' value represents the class width, which is the difference between the upper and lower boundaries of the class. For the interval 11-15, the class width is 5.

What does the 'Sigma fme' value represent in the formula for median?

Sigma fme is the cumulative frequency of all classes before the median class. In this case, the sum of frequencies before the median class is 12 + 8 = 20.

How is the median calculated using the formula for grouped data?

The median for grouped data is calculated using the formula: median = TB + [(1/2n - Sigma fme) / fme] * c. By substituting the known values into the formula, the result is 12.17.

What is the final value of the median in this calculation?

The final value of the median is approximately 12.17, which is obtained after applying the formula and rounding the result.