12-3 Sector Area and Arc Length
Summary
TLDRIn this video, the instructor covers key concepts of sector area and arc length in circles. They explain how a sector represents a portion of a circle, with formulas for calculating the area and arc length based on central angles and radius. The video walks through examples, clarifying how to use the degree of the sector or arc, along with the formulas for area (πr²) and circumference (2πr), to compute these values. It also addresses the distinction between degrees and arc lengths, and includes instructions for calculating the area of a segment using the sector and triangle areas. The tutorial emphasizes simplification techniques and rounding for accurate results.
Takeaways
- 😀 A sector is a portion of a circle formed by two radii and the arc between them.
- 😀 The area of a circle is given by the formula PI * r^2, and the area of a sector is a fraction of this based on the angle.
- 😀 The formula for finding the area of a sector is: (degree of the sector / 360) * PI * r^2.
- 😀 To find the arc length, the formula is: (degree of the arc / 360) * 2 * PI * r, where the result is the fraction of the circumference corresponding to the angle.
- 😀 The degree of an arc measures the angle, while the arc length is the actual distance along the arc.
- 😀 When calculating the arc length, use the actual degree and radius of the circle, and the result should be in units of length (e.g., feet, inches).
- 😀 Arc lengths and angles are different: two arcs with the same degree measure can have different lengths if their circle radii are different.
- 😀 The area of a sector is also affected by the radius, so two sectors with the same angle can have different areas depending on the size of the circle.
- 😀 The area of a sector can be expressed in terms of PI or in decimal form, depending on whether the problem asks for an exact or approximate answer.
- 😀 When solving problems involving sectors, always simplify fractions before plugging them into formulas to avoid large, unwieldy numbers.
- 😀 The segment of a circle is the area between an arc and the chord that connects the endpoints of the arc, and it can be found by subtracting the area of the triangle from the sector area.
Q & A
What is a sector of a circle?
-A sector of a circle is a portion of the circle defined by two radii and the arc between them, often visualized as a 'slice' of the circle, such as a piece of pizza.
How do you calculate the area of a sector?
-The area of a sector is calculated by multiplying the area formula of a circle (πR²) by the fraction of the circle that the sector represents. This fraction is determined by dividing the central angle of the sector by 360.
If the central angle of a sector is 90 degrees, what fraction of the circle does the sector represent?
-A central angle of 90 degrees represents a quarter of the circle, since 90/360 equals 1/4.
What is the formula for arc length?
-The formula for arc length is (degree of the arc / 360) × 2πR, where R is the radius of the circle and the degree represents the central angle of the arc.
What is the difference between the length of an arc and the degree of the arc?
-The degree of an arc refers to the measure of the central angle, while the length of the arc is a physical distance measured in units like feet or inches. They are related but not the same.
How do you find the arc length when given a central angle of 90 degrees and a radius of 10 feet?
-For a 90-degree arc and a radius of 10 feet, the arc length is calculated as (90/360) × 2π(10) = 5π feet, or approximately 15.71 feet when rounded to the nearest hundredth.
How do you calculate the area of a sector with a given radius and central angle?
-To calculate the area of a sector, multiply the area formula for a circle (πR²) by the fraction of the circle corresponding to the central angle, which is the central angle divided by 360.
What does it mean to simplify the fraction (degree / 360) when calculating arc length or sector area?
-Simplifying the fraction makes the calculations easier and prevents dealing with large numbers. For example, simplifying 40/360 to 1/9 before multiplying by 2πR helps make the computation more manageable.
What is a segment of a circle, and how is it related to a sector?
-A segment of a circle is the area between the arc of the sector and the chord that connects the endpoints of the arc. To find the area of a segment, subtract the area of the triangle formed by the radii and the chord from the area of the sector.
How do you calculate the area of a triangle formed by the radii of a sector?
-The area of the triangle formed by the radii can be calculated using the formula 1/2 × base × height, or using trigonometry with 1/2 × side1 × side2 × sin(angle) between the sides.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Lingkaran [Part 3] - Panjang Busur dan Luas Juring

Materi Matematika Kelas 8: Lingkaran
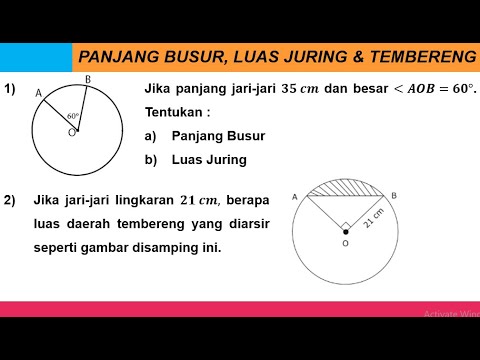
Cara Menghitung Panjang Busur, Luas Juring dan Luas Tembereng Pada Lingkaran

Cara Menghitung Panjang Busur dan Luas Juring Lingkaran

Mensuration (Full Topic)

Lingkaran (Bagian 4) - Panjang Busur, Luas Juring & Luas Tembereng | Soal dan Pembahasan SMP MTs
5.0 / 5 (0 votes)
