Cara Menghitung Panjang Busur, Luas Juring dan Luas Tembereng Pada Lingkaran

Summary

In this video, the process of calculating the arc length, sector area, and segment area of a circle is explained in detail. Starting with a circle where the central angle is 60 degrees and the radius is 35 cm, the steps for determining the arc length and sector area are shown. Additionally, the video covers how to calculate the segment area, by subtracting the area of the triangle formed by the radius from the sector area. The script provides clear formulas and simplifications, making the concepts of circle geometry accessible and easy to understand.

Takeaways

• 😀 The script discusses how to calculate arc length, sector area, and segment area in a circle.
• 😀 To find the arc length, use the formula: (central angle / 360) * (2 * Pi * radius).
• 😀 For the first example, the central angle is 60 degrees, and the radius is 35 cm, resulting in an arc length of approximately 36.67 cm.
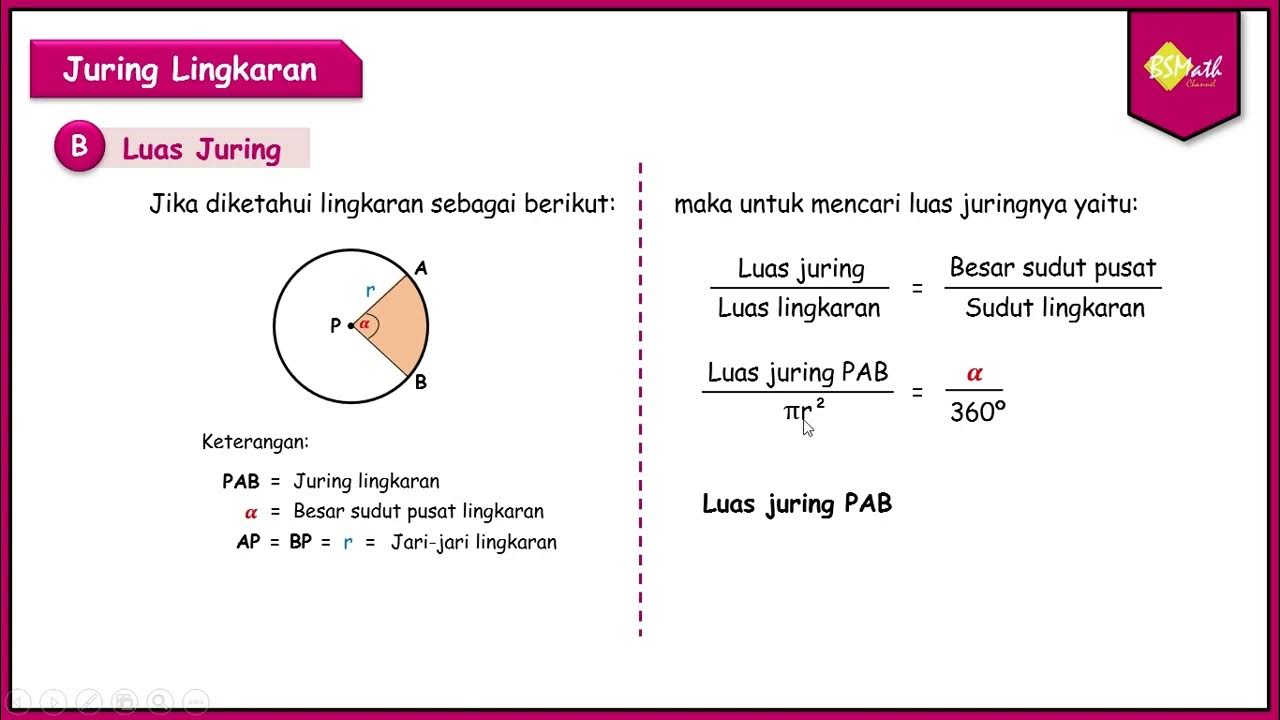
• 😀 The formula for sector area is: (central angle / 360) * (Pi * radius^2).
• 😀 In the first example, the sector area is calculated as approximately 641.67 cm².
• 😀 The segment area is found by subtracting the area of the triangle formed by the radius lines from the sector area.
• 😀 For the second example, the radius is 21 cm, and the angle is a right angle (90 degrees).
• 😀 To find the area of the sector in the second example, use the formula (90 / 360) * (Pi * 21^2), which gives approximately 346.5 cm².
• 😀 The area of the triangle formed in the second example is 220.5 cm², calculated using the formula (1/2) * base * height.
• 😀 The final segment area in the second example is the sector area minus the triangle area, resulting in 126 cm².

Q & A

What is the formula for calculating the length of an arc in a circle?

The formula for calculating the length of an arc is: (Central Angle / 360) * (2 * π * r), where the central angle is the angle at the center of the circle, and r is the radius of the circle.

How do you calculate the area of a sector (juring) of a circle?

To calculate the area of a sector (juring), use the formula: (Central Angle / 360) * (π * r^2), where the central angle is in degrees and r is the radius of the circle.

What is the difference between calculating the arc length and the sector area?

The arc length is calculated by multiplying the central angle with the circumference of the circle, while the sector area is calculated by multiplying the central angle with the area of the circle.

How is the arc length calculated for a central angle of 60 degrees and a radius of 35 cm?

For a central angle of 60 degrees and a radius of 35 cm, the arc length is calculated as (60/360) * (2 * π * 35), which simplifies to 36.67 cm.

How do you calculate the area of a circular sector with a central angle of 60 degrees and a radius of 35 cm?

To calculate the area of the sector, use the formula: (60/360) * (π * 35^2). This gives an area of 641.67 cm².

What is the formula to calculate the area of a segment (tembereng) of a circle?

The area of a segment is calculated by subtracting the area of the triangle formed by the two radii from the area of the sector.

How do you calculate the area of a segment when the central angle is 90 degrees?

For a central angle of 90 degrees and a radius of 21 cm, first calculate the area of the sector (346.5 cm²) and then subtract the area of the triangle (220.5 cm²) to get the segment area, which is 126 cm².

What is the method for calculating the area of a triangle in a circle when the triangle is a right triangle?

The area of the right triangle is calculated using the formula: 1/2 * base * height, where the base and height are the two radii of the circle.

What value of π should be used when the radius is a multiple of 7, such as 35 or 21?

When the radius is a multiple of 7, use π = 22/7 for simpler calculations.

Why is the central angle divided by 360 degrees when calculating the arc length and area of a sector?

The central angle is divided by 360 degrees because 360 degrees is the total angle in a full circle, so dividing the central angle by 360 gives the fraction of the circle that corresponds to the arc or sector.