Lingkaran (Bagian 4) - Panjang Busur, Luas Juring & Luas Tembereng | Soal dan Pembahasan SMP MTs

Summary

This educational video script focuses on teaching the concepts of arc length, sector area, and ring area in mathematics. It explains how to calculate the arc length using the formula (θ/360) * 2πr and sector area with the formula (θ/360) * πr^2, where θ is the central angle in degrees and r is the radius. The script also covers the calculation of ring area by subtracting the area of a triangle from the sector area. Practical examples are provided to illustrate these concepts, including the use of π ≈ 22/7 for calculations and solving problems involving specific angles and radii. The video aims to help students understand and apply these mathematical formulas effectively.

Takeaways

• 📏 The length of an arc on a circle can be calculated using the formula: (angle / 360) × (circumference), where circumference = 2πr.
• 📐 The area of a sector (juring) is found by the formula: (angle / 360) × (area of the circle), where the area of the circle = πr².
• ➖ To find the area of a segment (tembereng), subtract the area of the triangle from the area of the sector.
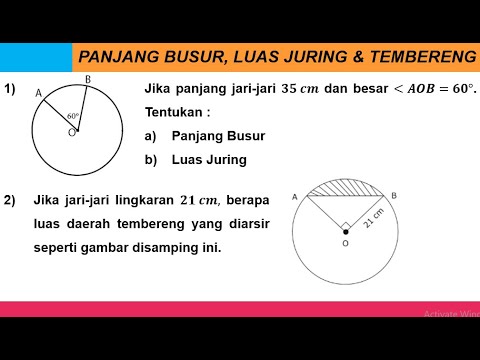
• 🔢 An example problem calculates the arc length using an angle of 108°, with a radius of 5 cm, resulting in an arc length of 9.42 cm.
• 📝 The area of a sector with the same angle (108°) and radius 5 cm is calculated as 23.5 cm².
• 📊 Another example uses a 72° angle and radius of 7 cm to calculate the arc length as 8.8 cm and the sector area as 30.8 cm².
• 🔺 To find the area of a segment in a circle with a right-angled triangle, first find the area of the sector and subtract the triangle's area.
• 🎯 A shortcut formula to calculate the area of a segment can be used, but understanding the core concepts is important for flexible problem-solving.
• 🖋️ A final example shows how to calculate the shaded area in a shape resembling a leaf by using a sector and triangle subtraction approach.
• 🔍 For complex shapes, using the Pythagorean theorem can help find the dimensions needed to calculate areas like segments and sectors.

Q & A

What is the formula to calculate the length of an arc?

The formula to calculate the length of an arc is given by \( \text{Arc length} = \frac{\theta}{360} \times 2\pi r \), where \( \theta \) is the central angle in degrees and \( r \) is the radius of the circle.

How is the area of a sector calculated?

The area of a sector is calculated using the formula \( \text{Area of sector} = \frac{\theta}{360} \times \pi r^2 \), where \( \theta \) is the central angle in degrees and \( r \) is the radius of the circle.

What is the difference between the formula for arc length and the formula for the area of a sector?

The formula for arc length involves multiplying the central angle by the circumference of the circle, while the formula for the area of a sector involves multiplying the central angle by the area of the circle.

How do you find the area of a circular segment?

The area of a circular segment is found by subtracting the area of the corresponding triangle from the area of the sector. The formula is \( \text{Area of segment} = \text{Area of sector} - \text{Area of triangle} \).

What is the significance of the number 360 in the formulas for arc length and sector area?

The number 360 signifies the total number of degrees in a circle, and it is used as a denominator to find the fraction of the circle's circumference or area that the arc or sector represents.

How is the circumference of a circle calculated?

The circumference of a circle is calculated using the formula \( \text{Circumference} = 2\pi r \), where \( r \) is the radius of the circle.

What is the purpose of using the approximation 22/7 for pi in the calculations?

The approximation 22/7 for pi is used to simplify the calculations when the exact value of pi (approximately 3.14159) is not necessary or when a more precise value is not available.

Can you provide an example of how to calculate the length of an arc given a central angle and radius?

Sure, if you have a circle with a radius of 5 cm and a central angle of 108°, the length of the arc would be calculated as \( \text{Arc length} = \frac{108}{360} \times 2 \times \frac{22}{7} \times 5 \), which simplifies to approximately 9.42 cm.

How do you calculate the area of a sector if the radius is 7 cm and the central angle is 90°?

For a sector with a radius of 7 cm and a central angle of 90°, the area is calculated as \( \text{Area of sector} = \frac{90}{360} \times \pi \times 7^2 \), which simplifies to approximately 38.5 square cm.

What is the concept behind the formula for the area of a circular segment?

The formula for the area of a circular segment is based on the idea that the segment is part of the circle that lies between the chord (the straight line connecting two points on the circle) and the circumference of the circle.

Outlines

00:00

📐 Introduction to Arc Length, Sector Area, and Segment Area

This paragraph introduces the concepts of arc length, sector area, and segment area in the context of a circle. It explains how to calculate the arc length using the formula Alpha/360 * circumference of the circle, where Alpha is the central angle in degrees. The circumference formula is given as 2 * pi * r. For sector area, the formula is pi * r^2 * Alpha/360. The segment area is calculated by subtracting the area of triangle OAB from the sector area. The paragraph also provides an example problem to demonstrate how to calculate the arc length and sector area using these formulas.

05:04

🔍 Detailed Calculation of Arc Length and Sector Area

This paragraph delves deeper into the calculations of arc length and sector area with a specific example. It shows how to use the formulas for arc length (Alpha/360 * 2 * pi * r) and sector area (pi * r^2 * Alpha/360) with given values for Alpha and r. The paragraph includes step-by-step calculations, using approximations for pi, to find the arc length and sector area. It also touches on the concept of segment area by subtracting the area of a triangle from the sector area, providing a method to calculate the area of a segment within a circle.

10:04

🌟 Advanced Problems on Circle Geometry

The final paragraph presents more complex problems involving the calculation of segment areas and other related geometrical shapes within a circle. It introduces a method to calculate the area of a quarter-circle minus the area of a triangle, using formulas that involve pi and the radius of the circle. The paragraph also demonstrates how to calculate the area of a design that resembles a leaf shape by using the formula for a quarter-circle minus the area of a triangle. Additionally, it shows how to calculate the area of a design that looks like a batik or flower pattern by using the Pythagorean theorem to find the diameter of a circle and then applying the formula for the area of a segment.

Keywords

💡Chord

A chord in geometry is a line segment whose endpoints both lie on a circle. In the context of the video, the term 'chord' is central to understanding the concepts of the circle's properties. The script discusses how to calculate the length of a chord, particularly when it is part of a circle's circumference. An example from the script is 'panjang busur', which translates to 'length of the chord', where the formula involves the central angle and the circumference of the circle.

💡Arc

An arc is a portion of the circumference of a circle, bounded by two points on the circle and the line segments that connect them to the center of the circle. The video script explains how to find the length of an arc using the formula which relates the arc length to the central angle in degrees, the circumference of the circle, and the value of pi. For instance, the script mentions 'panjang busur' which is used to calculate the length of an arc based on a given angle.

💡Sector

A sector of a circle is the region bounded by two radii and an arc lying between the radii. The script discusses the area of a sector, which is a key concept in understanding the video's theme of circle geometry. The area of a sector is calculated using the formula that involves the radius of the circle and the central angle in degrees. An example from the script is 'luas juring', which refers to the area of a sector, calculated by taking a fraction of the total area of the circle based on the angle.

💡Circumference

The circumference of a circle is the total length of the circle's edge. It is a fundamental concept in circle geometry and is used in various calculations related to circles, such as the length of an arc or the area of a sector. The script mentions the formula for the circumference as '2 * pi * r', where 'r' is the radius of the circle. This formula is used to calculate the total length of a circle from which parts, like arcs, can be determined.

💡Central Angle

A central angle of a circle is an angle whose vertex is at the center of the circle and whose sides pass through two points on the circle. The video script uses the concept of the central angle to explain how to calculate the length of an arc and the area of a sector. The central angle is crucial in determining the proportion of the circle that an arc or sector represents, as shown in the script where the formula for arc length and sector area includes the central angle.

💡Area

Area, in geometry, refers to the size of a two-dimensional surface and is a key concept in the video's discussion of circle properties. The script explains how to calculate the area of a sector and the area of a segment (the region between two chords). The area of a sector is calculated using the formula that involves the radius and the central angle, while the area of a segment is found by subtracting the area of a triangle from the area of a sector.

💡Segment

A segment in circle geometry refers to the region between two chords, including the area inside the minor arc and outside the major chord. The script discusses how to calculate the area of a segment, which is an important concept when dealing with parts of a circle. The area of a segment is calculated by subtracting the area of a triangle from the area of a sector, as illustrated in the script where the formula for the area of a segment is given.

💡Triangle

A triangle is a polygon with three edges and three vertices. In the context of the video, triangles are used in the calculation of the area of a segment. The script mentions a right-angled triangle formed by the radius and the chords, which is used to apply the Pythagorean theorem to find the length of the hypotenuse, which is part of the calculation for the area of a segment.

💡Pythagorean Theorem

The Pythagorean theorem is a principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. The script uses this theorem to calculate the length of the diameter of a circle, which is then used to find the radius and subsequently the area of a segment.

💡Pi (π)

Pi, often denoted by the Greek letter 'π', is a mathematical constant that represents the ratio of a circle's circumference to its diameter. The script mentions 'pi' in the formulas for calculating the circumference and the area of a circle, which are fundamental to understanding the properties of circles. The value of pi is approximately 3.14159, and it is used in various calculations throughout the video.

Highlights

Introduction to arc length, sector area, and segment area calculation in circles.

Arc length is the curved line on the circumference of a circle, defined as part of the circumference between two points.

Formula for arc length: Arc length = (Alpha / 360) * Circumference (2πr).

Formula for sector area: Sector area = (Alpha / 360) * Area of circle (πr²).

Segment area is found by subtracting the area of triangle OAB from the sector area AOB.

Example calculation: Find the arc length and sector area for a given angle of 108° and radius of 5 cm.

Step-by-step process of simplifying the equation to get an arc length of 9.42 cm and sector area of 23.55 cm².

Calculation of arc length and sector area for a circle with an angle of 72° and radius of 7 cm.

Result of arc length calculation: 8.8 cm for a circle with a 72° angle.

Formula for segment area: Segment area = Sector area - Triangle area, demonstrated for a 90° angle.

Explanation of shortcut formula for segment area: L = (2/7) * r².

Introduction of more complex problems involving quarter circles and other geometrical shapes.

Example of using Pythagoras’ theorem to find the diameter of a circle in a complex problem.

Demonstration of solving problems involving multiple segments or areas in geometrical shapes like flowers or batik patterns.

Final wrap-up, summarizing the methods for finding arc length, sector area, and segment area in various circle-related problems.

Transcripts

Hai assalamualaikum warahmatullahi

wabarakatuh Selamat datang di

pembelajaran matematika bersama delfini

di

Hai pada video kali ini kita akan

membahas mengenai panjang busur luas

juring dan luas tembereng nah sebelumnya

kita sudah mempelajari mengenai

unsur-unsur lingkaran ya panjang busur

disini merupakan garis lengkung yang

terletak pada lingkaran ya di sini

berarti yang termasuk panjang busur

sering ini ya Ini namanya busur AB Nah

untuk mencari panjang busur ini bisa

kita cari dengan rumus Alpha per 360

derajat dikali dengan rumus keliling

lingkaran rumus keliling lingkaran itu

adalah dua PR Kepler tip panjang busur

sama dengan Al paper 360 derajat dikali

2 PR sedangkan luas juring nah luas

juring itu ini ya daerah yang berwarna

merah

Hai Nah itu bisa kita cari dengan rumus

10 paper 360 derajat dikali rumus luas

lingkaran yaitu PR kuadrat

Hai kayak gini perbedaannya kalau

panjang busur itu apa per 360° nya

dikali dengan rumus keliling lingkaran

kalau luas juring itu rumusnya Al paper

360 derajat dikali rumus luas lingkaran

Sedangkan untuk mencari luas tembereng

itu bisa kita cari dengan rumus luas

juring aob dikurangi luas segitiga oab

Nah di sini ya Inikan Juring itu inikan

nabati luas juring aob ini dikurangi

luas segitiga ini segitiga oab itu udah

luas tembereng untuk memahaminya

perhatikan contoh berikut ini Tentukan

panjang busur dan luas juring pada

gambar berikut Nah kita akan cari

panjang busur terlebih dahulu ya

rumusnya adalah yakni kira singkat PB ya

PB = wallpaper 360° di

* 2-tier nah di sana alphanya adalah

sudutnya ini ya 108° kayak kita tulis

108° far 360 derajat dikali 2 PR adisana

airnya adalah 55 bukan merupakan

kelipatan 7 maka kita gunakan peyang

3,14 sehingga dua kali 3,14 dikali 5

selanjutnya ini kita Sederhanakan nih

108° part 360° kita bagi dengan 36 ya

108 dibagi 36 itu dapat tiga 360° dibagi

36 itu dapat 10 ya Jadi ini 3/10 di kali

ini dua kali 5-10 10 kali 3,14 yaitu 31

koma empat Nah kayak gini kita

operasikan tiga kali tiga 1,4 yaitu 94

koma dua persepuluh sehingga jawabannya

adalah 9,4 2qe ketemu nih panjang

busurnya adalah 9,4 2 cm

painting selanjutnya kita akan cari luas

juringnya Nah berarti

Hai ini tinggal diganti aja ya Kalau

tadi dikali dengan luas keliling

lingkaran kalau luas juring dikali

dengan luas

Hai lingkaran sehingga 3/10 dikali b r

kuadrat 3,14 dikali lima kuadrat

Hai maka 3/10 dikali nah ini hasil dari

25 5 kuasnya 25 ya 25 kali 3,14 yaitu

78,5 sehingga ini kita operasikan tiga

dikali 78,5 yaitu 235 koma lima

bersepuluh 3 jawabannya adalah 23,5 5 cm

persegi ake panjang musuhnya sudah

ketemu 9,4 02 dan luas juringnya adalah

23,5

e-cash selanjutnya nah sebuah lingkaran

dengan sudut poq itu besarnya 72° dan

panjang Oki yaitu 7 cm Hitunglah panjang

busur PQ dan luas juring poq Oke kita

cari dulu panjang busur ya mati disini

PB itu sama dengan wallpaper 360°

alphanya itu ada 72° ya 72° Ver 360

derajat dikali 2 PR di sana airnya

adalah okiya yaitu 7 cm Nah kita gunakan

peyang 22/7 jadi 2 dikali 26 juh ini

kita coret ya kemudian 72° per 360° kita

Sederhanakan jadi 1/5 ya kali dua dikali

dua yaitu

44 sehingga ini 44 dibagi lima yaitu 8,8

cm Oke temukan panjang busurnya Sekarang

kita cari luas juringnya kayaknya kita

langsung aja ya karena masih yang sama

lingkarannya betis 1/5 dikali b r

kuadrat 22/7 dikali 49 ya Nah ini kita

coret 29 dibagi 7 dapat 7 sehingga ini

1/5 dikali 154-156 dibagi lima dapat

30,8 cm2 akeh mudah bukan kayak mudah ya

Oke selanjutnya kita akan mencari luas

tembereng eh tembereng itu adalah unsur

lingkaran ini ya luas daerah yang

berwarna kuning Nah di sini diketahui

ada jari-jarinya itu adalah to

cm nah rumus dari luas tembereng itu

adalah luas juring dikurangi luas

segitiga ya berarti di sini kita akan

cari dulu luas juringnya nih Oke kita

tulis disini luas tembereng sama dengan

luas

Hai luas juring disini jurinya juring

QPR ya berarti wallpaper 360 derajat

dikali PR kuadrat dikurangi buah

segitiga QPR

ngopi kek disini alphanya adalah 90° ya

karena ini merupakan segitiga siku-siku

nah ini adalah besarnya 90° berarti 90°

per 360 derajat dikali 22/7 kali tujuh

kali tujuh ini kita coret sehingga ini

kesederhanaan dulu 90° per 360° kita

bagi 90 ya 90 bagi 91 360° dibagi 90

adalah empat jadi ini 1/4 dikali 22 kali

tujuh yaitu 154 nah 154 dibagi empat

dapat 38,5 ini adalah luas juringnya ya

Berarti sekarang tinggal di kurang luas

segitiga nah rumus dari luas segitiga

itu adalah alas kali tinggi per dua dari

sini batik yang jadi alasnya adalah 7

yang jari-jari p r i

tingginya adalah q-p itu 7 juga sehingga

disini tujuh kali tujuh per dua yaitu 49

dibagi dua adalah 24,5 sehingga 38,5

dikurangi 24,5 adalah 14 cm

Hai persegi ke sebetulnya ini ada cara

cepatnya ya rumus untuk mencari luas

tembereng itu cara cepatnya l = 2 atau 7

r kuadrat tapi kembali lagi kita harus

paham dulu konsepnya ya Karena tidak

selamanya rumus cepat ini bisa digunakan

Jadi kita tetap harus tahu konsepnya ini

kalau kita gunakan rumus cepat l = 2

atau tujuh kali tujuh kuadrat itu sama

dengan 27 kali 49 dicoret dapat 77 ke-2

14 sudah dapat ketemu luas tembereng 14

cm kayak kita lanjutkan ke soal

berikutnya Nah di sini ada bentuk soal

gambar ya jadi tanyakan luas daerah yang

diarsir kayak untuk soal yang pertama

ini ini bentuknya kayak seperti daun ya

untuk mencarinya kalau kita lihat disini

ini merupakan seperempat lingkaran ya

Hai nah ini ini luas tembereng ya

Hai nama kakak untuk mencari luas daerah

yang diarsir ini kita bisa pakai rumus

luas seperempat lingkaran dikurangi luas

segitiga Nahwa seperempat lingkaran

berarti seperempat dikali PR kuadrat

dikurangi alas kali tinggi itu kan

sama-sama jari-jari ya Jadi ini kita

tulis r kuadrat per dua selanjutnya

Hai ini seperempat PR kuadrat dikurangi

x kuadrat per dua ini bisa kita tulis

juga dengan 1/2 r kuadrat ya Sehingga

biar rumusnya enggak terlalu ribet kita

keluarin nih yang samanya batia semuanya

apa ini x kuadrat ya ekornya kita

keluarin sehingga yang dalam kurungnya

ini 1/4 phi dikurang 1/2 kayak gini kita

bisa gunakan rumus ini Ken sekarang kita

masukkan angka-angkanya jari-jarinya

adalah 10 kayak maka disini 10 kuadrat

dalam kurung 1/4 dikali 3,14 dikurangi

1/2 nah 10 kuadrat adalah 100 kemudian

3,14 dibagi empat dapat 0,78 5 dikurangi

setengah-setengah itu 0,5 Hei maka 100

dikali hasil dari 0,7 85 dikurangi 0,5

adalah 0,2

285 ya kemudian kalikan dengan 100

sehingga kita dapatkan hasilnya adalah

28,5 cm2

10 selanjutnya kita lihat di sana luas

tembereng yaitu ada dua buah ya maka

kita tinggal kalikan dua saja 28,5

dikali dua yaitu 57 sentimeter per segi

keju banyak yang a ok

rezeki

hai hai

the song berikutnya Perhatikan gambar di

bawah ini ya jika panjang sisi persegi

itu adalah 14 cm Hitunglah luas daerah

yang diarsir ke ini bentuknya seperti

batik ya atau bunga nah caranya sama

seperti cara menjawab soal sebelumnya

sekarang Perhatikan gambar dibawah ini

nah disini untuk memudahkan perhitungan

kita buat lingkaran seperti gambar ini

dulu ya Nah sehingga kita bisa cari

panjang diameter lingkaran ini yang

garis merah dengan menggunakan teorema

Pythagoras sehingga ini misalkan

diameternya itu D = akar dari tujuh

kuadrat ditambah 7 kuadrat nah batin

dijadikan sisi miring ya Sehingga D ini

itu sama dengan

i7 akar2 ya Oke sekarang kita cari

jari-jarinya jari-jari itu adalah

setengah dari diameter sehingga 7-akar

dua dibagi dua yaitu 72-akar dua Nah

selanjutnya disini kita bisa hitung luas

tembereng nya pakai rumusnya cepat 27 r

kuadrat sehingga 2/7 dikali 72-akar dua

dikuadratkan jawabannya adalah

i7 cm2 Oke luas daerah yang diarsir

dapat dihitung dengan mengalikan jumlah

tembereng dengan luas masing-masing

tembereng Nah di sini ada 8 buaya

temberengnya sehingga ke luas

keseluruhan adalah delapan dikali tujuh

sentimeter persegi yaitu 56 cm persegi

jadi luas yang diarsir adalah 56 cm

persegi

Hai guys sekian pembahasan kali ini

tentang panjang busur luas juring dan

luas tembereng Oke jangan lupa simak

terus video-video berikutnya mengenai

video pembelajaran matematika kelas 8

hanya di channel math-lab

wassalamu'alaikum warahmatullahi

wabarakatuh ya

hai hai

Hi Ho