Mensuration (Full Topic)

Summary

In this educational YouTube video, Chamba Jacob introduces the concept of 'measuration', focusing on geometrical measurements like perimeter, circumference, volume, and area. He explains these through examples of shapes such as rectangles, circles, and pyramids, providing formulas and step-by-step calculations. Jacob also covers the calculation of arc length and sector area in circles, and the volume of cones and pyramids. The video is designed to help viewers understand and apply these measurements in various geometrical contexts.

Takeaways

• 😀 The video discusses the concept of 'measuration', which involves measuring different geometrical properties.
• 📏 The video defines 'perimeter' as the outline or path around a shape, and 'circumference' as the perimeter of a circle.
• 🔢 To calculate the perimeter of a rectangle, you sum all its sides, which can be expressed as 2*(length + breadth).
• 📐 The area of a rectangle is found using the formula length times breadth, and for a circle, it's \( \pi \times \text{radius}^2 \).
• 🔄 When dealing with a circle, the video explains how to calculate the circumference using \( 2 \times \pi \times \text{radius} \), with options to use either the decimal or fraction form of \( \pi \).
• ⭕ The video introduces the concept of a sector of a circle and explains how to find its arc length and area.
• 🔺 For pyramids, the volume is calculated using the formula \( \frac{1}{3} \times \text{base area} \times \text{height} \), and the total surface area includes the sum of the areas of all faces.
• 📦 The video demonstrates how to calculate the volume of a cone using \( \frac{1}{3} \times \pi \times \text{radius}^2 \times \text{height} \).
• 🔍 The script includes a practical example of finding the volume of a cone with a missing part, using the concept of similarity and congruence.
• 📝 The presenter encourages viewers to remember units when calculating areas and volumes, emphasizing the importance of precision in measurements.

Q & A

What is the definition of menstruation as mentioned in the script?

Menstruation, as incorrectly mentioned in the script, is described as the act of measuring, which is not accurate. The correct term intended might be 'measurement', which involves calculating properties like perimeter, circumference, volume, and area of shapes.

What is the formula for calculating the perimeter of a rectangle?

The formula for calculating the perimeter (P) of a rectangle is P = 2 * (length + breadth). If the length is 4 centimeters and the breadth is 2 centimeters, the perimeter would be P = 2 * (4 + 2) = 12 centimeters.

How is the circumference of a circle different from its perimeter?

In the script, it's mentioned that the circumference is the perimeter of a circle. Technically, 'circumference' is the term specifically used for the perimeter of a circle, while 'perimeter' is a more general term used for the outline of any shape.

What is the formula used to calculate the area of a rectangle?

The formula to calculate the area (A) of a rectangle is A = length * breadth. Using the values from the script, if the length is 4 centimeters and the breadth is 2 centimeters, the area would be A = 4 * 2 = 8 square centimeters.

What is the formula for calculating the circumference of a circle?

The formula for calculating the circumference (C) of a circle is C = 2 * π * r, where 'r' is the radius of the circle. Using the value π ≈ 3.142, if the radius is 4 centimeters, the circumference would be C = 2 * 3.142 * 4 = 25.136 centimeters.

How do you calculate the area of a circle?

The area (A) of a circle is calculated using the formula A = π * r^2, where 'r' is the radius of the circle. If the radius is 4 centimeters, the area would be A = 3.142 * 4^2 = 50.272 square centimeters.

What is the formula for finding the arc length of a sector of a circle?

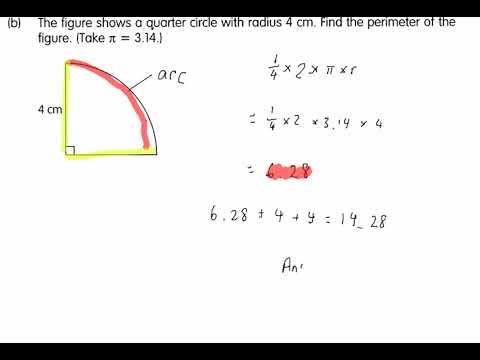
The formula for finding the arc length (L) of a sector of a circle is L = (θ/360) * 2 * π * r, where 'θ' is the central angle in degrees and 'r' is the radius of the circle. If θ is 90 degrees and r is 4 centimeters, the arc length would be L = (90/360) * 2 * 3.142 * 4 = 6.28 centimeters.

How is the area of a sector of a circle calculated?

The area (A) of a sector of a circle is calculated using the formula A = (θ/360) * π * r^2, where 'θ' is the central angle in degrees and 'r' is the radius. If θ is 90 degrees and r is 4 centimeters, the area of the sector would be A = (90/360) * 3.142 * 4^2 = 12.57 square centimeters.

What is the formula for calculating the volume of a pyramid?

The formula for calculating the volume (V) of a pyramid is V = (1/3) * base area * height. If the base is a rectangle with length 3 centimeters and breadth 7 centimeters, and the height is 5 centimeters, the volume would be V = (1/3) * 3 * 7 * 5 = 35 cubic centimeters.

How do you calculate the volume of a cone?

The volume (V) of a cone is calculated using the formula V = (1/3) * π * r^2 * h, where 'r' is the radius of the base and 'h' is the height. If the radius is 2 centimeters and the height is 6 centimeters, the volume would be V = (1/3) * 3.142 * 2^2 * 6 ≈ 25.13 cubic centimeters.

Outlines

00:00

📹 Introduction to Channel and Menstruation Topic

In this introductory segment, the host welcomes viewers to the YouTube channel, encouraging them to subscribe, like, and comment. The video then introduces the topic of 'mensuration' as the process of measuring, with examples such as perimeter, circumference, volume, and area. The speaker briefly touches on shapes, focusing on a rectangle, and begins explaining the concepts of perimeter and circumference, highlighting that circumference refers specifically to circles.

05:01

🔢 Finding Perimeter and Area of Shapes

This paragraph expands on how to calculate the perimeter and area of basic shapes, starting with a rectangle. The speaker provides a step-by-step guide to find the perimeter by adding the lengths of all sides, followed by calculating the area using the formula length times breadth. The explanation emphasizes the importance of correct units, especially for area (square centimeters). The speaker then introduces circles, explaining how to find the circumference using the formula 2πr and comparing it to the perimeter of other shapes.

10:03

🔄 Working with Circles: Circumference and Area

Here, the focus is on the calculations involved in a circle. The speaker teaches how to find the circumference using the formula 2πr and clarifies that π can be expressed as either 22/7 or 3.142 depending on the context. The area of a circle is then discussed, with an explanation of the formula πr², and example calculations are provided. The segment also introduces the concept of a sector, explaining how to calculate the arc length and area of sectors using variations of the circumference and area formulas.

15:04

🔺 Exploring the Volume and Surface Area of Pyramids

This part of the video shifts focus to pyramids, where the speaker explains how to find the volume using the formula (1/3) × base area × height. An example pyramid with dimensions is used to demonstrate the process, emphasizing the importance of identifying the shape of the base (rectangle or square). The concept of total surface area is introduced, with instructions to calculate the area of all triangular faces and the base.

20:05

🌀 Working with Cones: Volume and Surface Area

In this paragraph, the speaker explains how to calculate the volume of a cone using the formula (1/3) × π × r² × height. The example used involves a cone with specific dimensions (radius and height). The speaker demonstrates the steps for calculating the volume and touches on finding the total surface area of the cone, emphasizing the formula for the base (a circle) and explaining how to incorporate it into the overall volume calculation.

25:05

📏 Advanced Cone Calculations and Congruence Concepts

This paragraph delves into more complex problems involving cones, such as finding the volume of a frustum (a cone with the top cut off). The speaker explains how to use the principles of similarity and congruence to solve for unknown dimensions, then demonstrates how to subtract the volume of the smaller cone from the larger one. The segment concludes with calculating volumes and showing how the remaining volume represents the frustum, followed by a reminder to check other relevant videos for additional explanations.

Keywords

💡Menstruation

The term 'menstruation' in the context of the video is mistakenly used and should correctly be 'measurement'. Measurement is the process of determining the size, amount, or degree of something. In the video, it refers to the mathematical operations used to calculate dimensions such as perimeter, area, volume, and circumference. The script discusses various geometrical shapes and how to measure their attributes, making 'measurement' a central concept for understanding the video's educational content.

💡Perimeter

Perimeter refers to the total length around a two-dimensional shape, which is the sum of all its sides. In the video, the concept is introduced with a rectangle, where the perimeter is calculated by adding together the lengths of all four sides. This is a fundamental concept in geometry and is essential for understanding how to measure the boundaries of shapes, as demonstrated in the script with the formula P = 2l + 2w for a rectangle.

💡Circumference

Circumference is the perimeter of a circle, or the distance around it. The video explains that while the term 'perimeter' is used for polygons, 'circumference' is specific to circles. The script provides the formula for calculating circumference as C = 2πr, where 'r' is the radius of the circle. This concept is crucial for understanding the measurement of circular objects and is used in the video to teach viewers how to find the circumference of a circle given its radius.

💡Area

Area is the amount of two-dimensional space enclosed within the boundary of a shape. The video discusses how to calculate the area of a rectangle using the formula A = l × w, where 'l' is the length and 'w' is the width. Area is an important concept in geometry as it helps in understanding the size of shapes and surfaces, which is a key theme in the educational content of the video.

💡Volume

Volume is the measure of the space occupied by an object or substance. In the video, volume calculations are discussed for both pyramids and cones, using formulas that involve the area of the base and the height of the shape. Understanding volume is essential for determining the capacity of three-dimensional objects, which is a significant part of the video's educational focus.

💡Rectangle

A rectangle is a quadrilateral with four right angles. The video uses the rectangle to explain the calculation of perimeter and area, which are fundamental geometrical properties. The script provides a clear example of how to calculate these measurements for a rectangle, which is a basic shape in geometry and a common subject in educational content related to shapes and measurements.

💡Circle

A circle is a round shape with all points at an equal distance from the center point. The video script explains how to calculate the circumference and area of a circle, using π (pi) in the formulas. Circles are fundamental in geometry, and understanding their properties is essential for learning about curved shapes and their measurements.

💡Sector

A sector is a portion of a circle enclosed by two radii and an arc. In the video, the concept of a sector is introduced when discussing the area and arc length of only a part of a circle. The script explains how to calculate the area of a sector using a formula that involves π, the radius, and the central angle, which is a specific application of geometrical measurements.

💡Pyramid

A pyramid is a three-dimensional solid object with a polygonal base and triangular sides that meet at a point called the apex. The video discusses how to calculate the volume of a pyramid, which is one-third the product of the base area and the height. Pyramids are an important shape in geometry, and learning to measure their volume is part of understanding three-dimensional space.

💡Cone

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex. The video explains the calculation of the volume of a cone, similar to a pyramid but with a circular base. The script uses the formula V = (1/3)πr²h to demonstrate this, which is a key concept in understanding the properties of conical shapes and their measurements.

💡Arc Length

Arc length is the distance along the curved part of a circle between two points on the circumference. The video script introduces arc length in the context of sectors of a circle, explaining how to calculate it using a proportion of the full circle's circumference. This concept is important for understanding measurements along curved lines and is a specific application within the broader theme of geometrical measurements.

Highlights

Definition of menstruation as the act of measuring, including perimeter, circumference, volume, and area.

Explanation of perimeter as the path that outlines a shape, with an example using a rectangle.

Differentiation between perimeter and circumference, with circumference specific to circles.

Introduction to volume and area, with a promise to discuss through examples.

Calculation method for the perimeter of a rectangle, including formula and example.

Formula for the area of a rectangle, demonstrated with an example.

Circumference of a circle defined and formula introduced.

Use of pi in calculations, with options for decimal or fraction form.

Calculation of the area of a circle, including the formula and an example.

Introduction to sectors of a circle and the concept of arc length.

Formula for calculating arc length, with an example using theta and pi.

Method for finding the area of a sector, including the formula and an example.

Transition to pyramids and the concept of volume, with the introduction of the formula.

Explanation of total surface area of a pyramid, including how to calculate it.

Introduction to cones and the formula for calculating their volume.

Practical example of calculating the volume of a cone with given radius and height.

Complex problem-solving involving the volume of a cone with an unknown height, using similarity and congruence.

Final calculation of the volume of a cone after determining the unknown height.

Encouragement to watch more videos on related topics and a call to action for likes and comments.

Transcripts

hello welcome to my youtube channel this

is

chamba jacob kindly subscribe and be

able to watch more videos

like share and also comment

okay today we'll try to look at uh

this topic measuration

we'll start with we start by defining

what

is menstruation so menstruation is the

act

of measuring so it just involves

measuring okay

so uh this is where you find things like

perimeter

conference volume and area

so when uh when dealing with

uh with the menstruation

you find shapes like this one this is

probably a rectangle

so but before we can even discuss more

on this rectangle which is over here

i would like us to talk about the

terminologies which are up here so

perimeter

so once you see this weight perimeter

what comes in your mind

all right so a perimeter is simply

the path outline

the shape so the path which outlines

the shape okay meaning

this path here here around

the shape you're talking about that's

perimeter and then the circumference

circumference is the perimeter of

a circle so we don't say perimeter to a

circle we say circumference so these

almost the same things now this applies

to the circle this one to

some other shapes apart from a circle

okay a volume and area there

we'll talk about this as we are we look

at the examples

so okay now about the parameter

so let's say they have been given this

shape and then they say find

the perimeter

so how do you find the perimeter of

this shape here very simple

let's say the breadth here is a 2

centimeters and

the length down here is 4

centimeters and they ask you to find the

perimeter what do you do

you just say 4 or you say p

is equal to 4 plus 4

plus 2 plus

2 or if you want you can say four plus

two plus four plus c

two so this is four plus four plus two

plus two because

we have this side plus this side plus

this side plus this side

which will give us the answer

uh to be 12 so you say 12 centimeters

it's more like it's the distance around

it

the figure okay or the shape that you've

been given

again at this same rectangle they may

ask you to find the

area this area how do you find the area

so area of a rectangle be given by the

formula

l times z b so a o times b

we know our ao is the length

which is four times our b which is the

predict

which is equal to two and when you

work out you find that your answer will

be eight

centimeters squared don't forget the

units they are very important

okay so we now

make a move to another shape

so the shape the shape is over here

this is a circle and under circle that's

where you find

questions like find the circumference

the circumference of circumference is

just

a perimeter around the circle this is a

pyramid around the sequence called

circumference

okay so when you want to find the

circumference

let's say you've been given the arrow

here okay

this arrow which is the radius between

maybe is equal to

four centimeters so if your radius is

equal to four centimeters

and they say find the circumference what

you basically do

here you say circumference

is equal to 2 pi

r so this is a formula circumference is

equal to

2 by r it depends

with the exams you are writing mostly

easy said you are given what to use if

we because there are two

options you can either use uh you can

use the

the the pi in the decimal form or

uh in the fraction form so in the

fraction form let's see 22 over 7

and in a decimal form it's 3.142 so

we're going to use the decimal

so say 2 times

3.142

times the radius is 4.

so we can punch these values

on our calculator so we say 2 multiplied

by 3.142 times z4

and the value will be equal to

25 per

centimeters so this is the value we

found

as our circumference so at this same

shape

a circle you can be asked to find the

area

okay of this circle so the area

of the circle you use the formula almost

the same

but you just remove a two

and you square the arrow you remove the

two you square there

are these are just formulas you must

keep them in your head

so what you do here we use

the same pie which is

3.142 times our radius we are given the

radius here

which is 4 4

and we say 4 squared here so we work out

things here

we say 3.142 times 4 squared

our answer will be equal to 50.272

centimeter squared

so that's our our answer so

under this same circle

you may you may be

given part of the circle not all of it

let's say

they've decided to give you something

like this

they cut this upper part is chopped out

and you've just been given this

down part okay or if you they want they

give you this

this part like this or this part is out

so what do you do what comes in your

mind

wow i'm dealing with the sector it looks

like this

so this is a sector over here okay

so you may be asked to find

some kind of the arc length like a

circumference

of a full circle now they want you to

find

that circumference of the chopped

uh the the part which is a which which

from here to here

okay part of a circle and we call it arc

length so how do you find that how do

you find that

so in order for you for us to find it we

use the formula almost the same formulas

almost these same formulas for

circumference

so for arc length we use the one for

circumference which goes like this

i'll leave some space for a purpose this

is the formula for

circumference but for arc length

we are going to put it something like

this

this this is

the total angle of the circle and on top

you put

pi i'll tell you where what pi means

let's say we have been taught that this

is a pi over here and the value of pi is

90 degrees while the radius which is

arrow

is four centimeters

like it was here it's four centimeters

and they say calculate the arc

length so how do you calculate the arc

length

so you get the values you are able to

see

theta is 90 degrees over 360

times two times pi is three

point one four two times

times uh what other thing i do times r

the radius which is equal to four

so you solve this on your calculator

before

actually before you so you you you get

your calculator

you can clean it up you can reduce the

values here 90 into

into 360 it's four so you remain with

something like this this can cancel so

remain with two multiplied by

three point one four uh

three point one four two so you get

calculated

two times two multiplied by three point

one four two

your va your answer will be equal to six

point two eight four

centimeters so this is a length

okay so on this same diagram

you can be asked to find the area so how

do you find the area

so for the area you use the same formula

for area

okay same formula for area so you say

area of the sector this will be area of

the sector

leave some space so the formula for area

of

the formula for for a circle sorry for

finding area of a circle

is this one so now since it's a sector

we're going to

add this what we added

here remember what we added here

is what we are going to add such that

we say pi is 90

e over 360 times

3.142 which is our

pi times 4 squared which is our radius

so here we can reduce

well something like this because 90 can

go into 360

times 3.142 times

four squared so these four go

this will remain with the one for here

so we can multiply now three point one

four

two three point one four two times the

four so three point one four two

times four we find that our answer will

be equal to twelve

point five six

eight centimeter square don't forget the

units

so this is how it do you do with the

sector as well as the

the the circle so now

we'll try to make a move to another

shape

which is uh which is uh

a pyramid so if you can see nicely this

is a pyramid

okay it's a pyramid over here

so once you see a pyramid what comes in

your mind

you find a volume so the formula for

finding volume

will be equal to area of

the base

times height

this is what you do when you want to

find volume of a pyramid

so you say area of the base you have to

be very careful here you check

what do you have here is it a rectangle

or

or a square down here so who

will assume we have a rectangle so we

say

area of of a rectangle we say l times a

b times the height so this

would be our formula actually we forgot

something here

it's supposed to be one over three one

over three

this is the formula we're supposed to to

use okay

so let's say we have uh

this side whoever seven centimeters

here we have three centimeters

five centimeters this is our height

okay and they ask us to find

uh the volume so how do you find the

volume here so for us to find the volume

here we use the formula

we say

volume is equal to what is the air what

is the base what base are we dealing

with is it a rectangle

or a square this is a rectangle because

this side and this side are different

you say

rectangle so we say one over three

okay length times the predict

times the height so in this case

we say what is our what is our length

our length will be will be equal to or

is

equal to is equal to three

the three which is here and what is our

bridges it's seven what is our height

is five okay under this same

shape you can be asked to find the total

surface

area total

surface area

so how do you find the total surface

area

it's a do finding area you find what we

call total surface

area so the total surface area or just

the surface area

meaning you check how many how many how

many

how many triangles you have this

triangle there is this also triangle

another one there another one there

so find the triangle of i mean the area

of each triangle this one this one

this one and this one so when you find

the area

add them you come and also add the area

of the

base here okay so you add all the areas

of each shape you're able to see

that's total surface area okay we make a

move we now go to

to a coin

so this is a cone over here hopefully

you're able to see it's a cone

so for the cone

for the cone

you have uh you have a formula for

finding volume

they ask you to find volume so volume is

equal to

almost the same almost the same you say

one over three

multiplied by area

of the base

times height

so this is what you do where you say

one over three times what is the area of

the base

if you can see what shape do you have

here it's a circle so area of this

formula for area of a circle you see by

r squared

times h which is the height

okay so now let's try to

pretend we have been given radius

as uh as uh

as uh two

centimeters and the height

here let's say the height is

uh is six centimeters and they say

calculate the volume so how do you find

the volume here

so the volume can be calculated using

the formula

we just we just found

this is the formula we use so say

one over three our pi is

three point one four two times our

radius

here is it's a two so it will be 2

squared times our height which is 6.

so we can now work out things 3 2 3 1

3 into 6 it's 2 so now we can multiply

here we say what

three point one four two times

two squared times two and the answer

will be equal to twenty

five point one three

six centimeter cubed remember the units

we are dealing with see

with uh with with uh

with it's a volume so remember the units

for what volume

it's supposed to be cubed up there so

our question

or the question here i've been given a

diagram on the

measurements so they want us to find

the volume so how do we find the volume

so remember first thing the formula

which is volume is equal to 1 over

3 multiplied by

area of the base since the base is a is

a circle so this is the area of the base

multiplied by height so this is the

volume uh the formula for volume

now we are dealing with it what we call

first term

so what you do you copy

you copy the

the the coin the way it is but you

finish it you pretend it's finished

so if you can see nicely here i'm

putting it as if

it's finished so the distance from here

to here the height is a

10 centimeters and what has been cut

here will say x we don't know the height

of what has been cut from here to here

so say from here

to here it's x from here to

here it's 10. so

and we have there the the radius here

which is three

here the radius is eight so what do we

do here we use the similarity and the

idea of similarity and congress

where i'll say the total height

of the bigger triangle will be

10 plus this

which we don't know we'll just say x so

say x over

we're using now the idea of similarity

and congruence

so this is the this x the small one here

will move with the bigger one okay over

the bigger

and then we come to the radius the small

radius within the

bigger radius down so now we can solve

for x

where i'll cross multiply we have 8x

is equal to 3 10 minus

x so

we distribute here of 30 plus 3x

we group the like terms so this is how

it will look like

and here it will be equal to 5

x which is equal to 36

so the value of x here is a 6

centimeters so we know that

here is it six centimeters

so we go to we now

try to find it the volume we know that

now

we know that the small cone

the part which has been cut it has got a

the height of

six centimeters and the radius is three

why is the the bigger cone

the bigger coin has got the height of uh

you say

10 plus c 6 it will be equal to

60 and the radius of 8 centimeters

so now we're going to find the volume of

this bigger

triangle i mean corn and the

volume of the small coin so come and

subtract the volume of the small coin

from the volume of the bigger

coin where we say volume is equal to 1

over 3

by r squared h

and here we put 3

multiplied by 3.142 times our radius is

8 centimeters we're dealing with a

bigger

bigger chord times our height

is in 16 so now we can solve here

on our calculator when we punch say

1 multiply by 3.314 multiplied by

8 squared times 16

it's giving us 3 to

[Music]

17.408

over 3 so when you divide by three

our answer will be equal to zero

one zero seven seven two

point four six nine

three three three now putting this in

three significant figures to be one

uh zero seven

zero centimeter

acute we're dealing with the the volume

so this is the volume

this is the volume of the bigger coin

so now try to find the volume of the

smaller coil

so let me put it here so it will be

let me cut and mark it so we're able to

see the small coin is over here

this is a small coin so use the formula

so what is our what is our

our pie pi is 3.142

what is our radius three so put square

there what is our height

is six we just found six here eighty-six

so now we can

we can solve here

three point one four two times uh

actually here we can cancel one

a three two and two three it's one three

two six is a

two so say

uh three pointy

one four two times the three squared

times the six what are we getting

one six nine point

six six eight centimeter cubed so this

is the volume of the

smaller uh

coin so we can also write it in uh

three significant figures so this is

what we have

actually in three significant figures

supposed to be seven here and that's 170

okay so

we now say the volume of the

bigger triangle i mean the volume of the

bigger

coin which is 170 minus minus

the one for the smaller one which is 1

770

so we can say

the value get now is equal to

900 centimeters squared

i'm cubed so this is the answer

so if you'd like to see to watch more

videos i've done the one for the

for the the pyramid you can watch i'll

put the link in the description below

and uh please share like my videos and

comment

okay the advice where you see that

we need to to do one or two things

thank you