CONVERTING A NORMAL RANDOM VARIABLE TO A STANDARD NORMAL VARIABLE AND VICE VERSA
Summary
TLDRThis tutorial explains the concept of Z-scores and how to convert a normal random variable into a standard normal variable. The Z-score is used to measure how far a data point is from the mean, in terms of standard deviations. The video covers key concepts, including interpreting Z-scores (positive, zero, or negative), calculating Z-scores using a formula, and finding areas under the normal curve. It provides practical examples, such as calculating Z-scores for test scores and lifespans, and discusses how to determine probabilities and percentages in a normal distribution. The tutorial is ideal for understanding the basics of normal distribution and statistical analysis.
Takeaways
- 😀 Z-scores represent the number of standard deviations a data point is from the mean of a normal distribution.
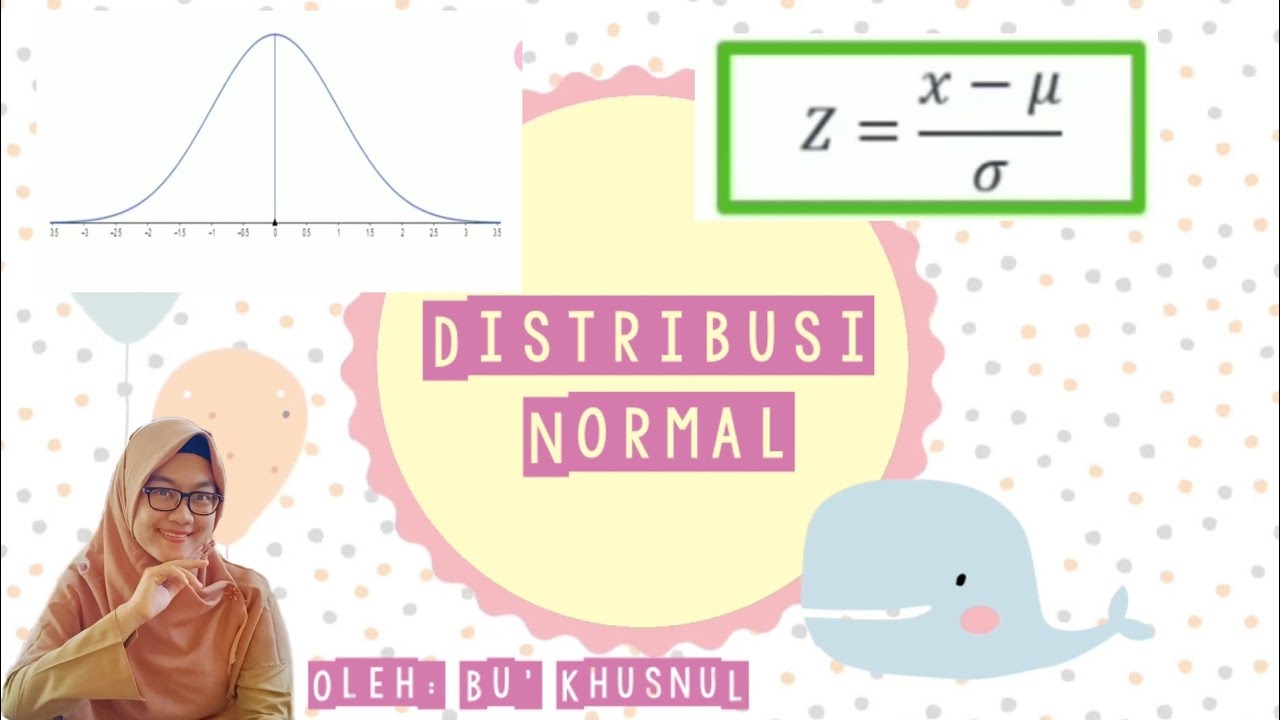
- 😀 The formula for calculating the z-score is: z = (x - μ) / σ, where x is the data value, μ is the mean, and σ is the standard deviation.
- 😀 A positive z-score indicates that the data value is above the mean, while a negative z-score indicates it is below the mean.
- 😀 A z-score of zero means the data point is exactly at the mean of the distribution.
- 😀 To calculate the z-score for a given x-value, subtract the mean from the x-value and then divide by the standard deviation.
- 😀 Z-scores help standardize data, allowing comparisons across different normal distributions with different means and standard deviations.
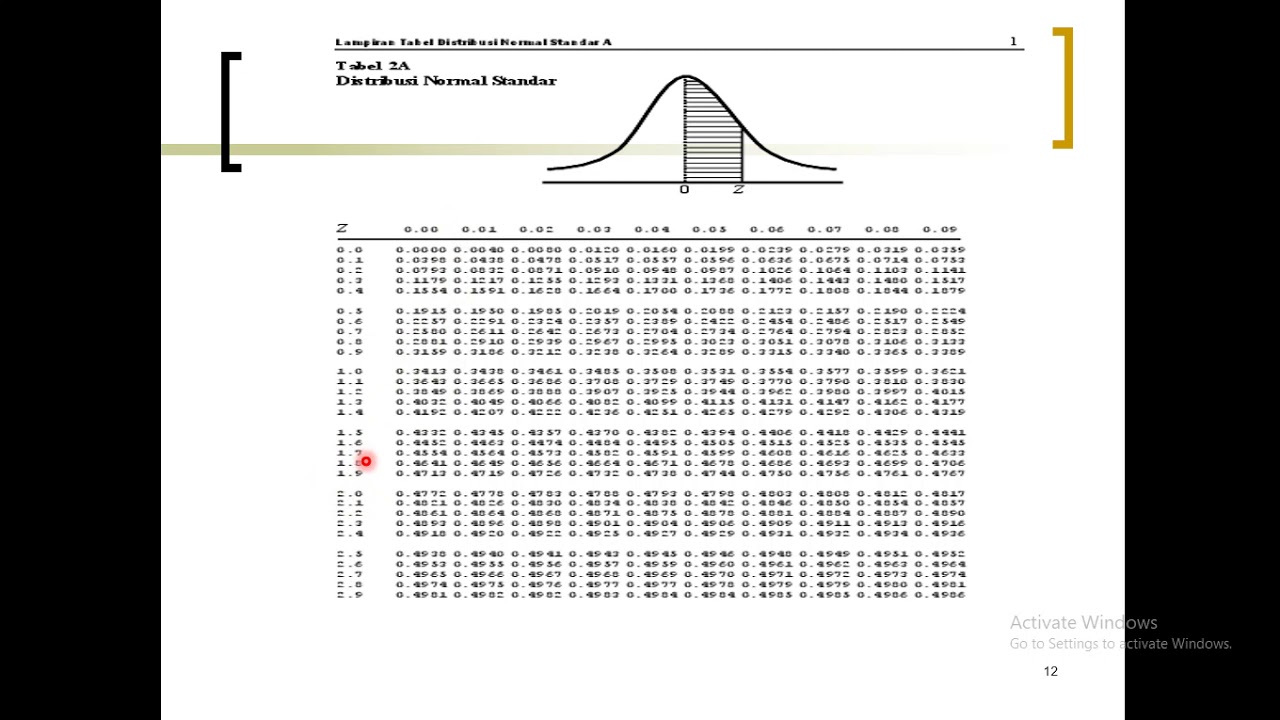
- 😀 The area under the normal curve between two z-scores can be found using standard z-tables, which provide cumulative probabilities.
- 😀 The z-score formula is used to transform a normal distribution into a standard normal distribution, which has a mean of 0 and a standard deviation of 1.
- 😀 Z-scores are useful for finding percentiles, probabilities, and determining how unusual or typical a given data point is within a distribution.
- 😀 Practical problems often involve calculating z-scores to find corresponding data values, such as determining the lifespan of a light bulb based on its z-score.
- 😀 To find the area under the curve between two values, calculate the z-scores for both and use the z-table to find the cumulative probability between them.
Q & A
What is a z-score, and why is it important in statistics?
-A z-score measures the distance between an individual data point and the mean of a normal distribution, expressed in terms of standard deviations. It is important because it allows us to standardize different data points for comparison, even if the data sets have different means or standard deviations.
How do you calculate a z-score?
-The z-score is calculated using the formula: z = (x - μ) / σ, where x is the data value, μ is the mean, and σ is the standard deviation of the distribution.
What does it mean if a z-score is positive, zero, or negative?
-If a z-score is positive, the value is above the mean. If the z-score is zero, the value is exactly at the mean. If the z-score is negative, the value is below the mean.
How do you interpret a z-score of -1.33?
-A z-score of -1.33 means the data value is 1.33 standard deviations below the mean.
Given a normal distribution with a mean of 16 and a standard deviation of 3, what is the z-score for a data value of 12?
-The z-score for a data value of 12 is calculated as: z = (12 - 16) / 3 = -1.33. This means the value is below the mean.
What is the area under the normal curve between z = 0 and z = 1.75?
-The area under the normal curve between z = 0 and z = 1.75 is approximately 0.4608, which means that about 46.08% of the data falls between these z-scores.
In the example where the mean is 50 and the standard deviation is 4, what is the z-score for a data value of 58?
-The z-score for a data value of 58 is calculated as: z = (58 - 50) / 4 = 2. This means the value is 2 standard deviations above the mean.
How do you find the value corresponding to a z-score of 1.2 if the mean is 842 hours and the standard deviation is 90 hours?
-The value corresponding to a z-score of 1.2 is calculated using the formula: x = z * σ + μ. So, x = 1.2 * 90 + 842 = 950 hours.
How do you interpret a z-score of -0.25 in the context of test scores?
-A z-score of -0.25 means the test score is 0.25 standard deviations below the mean. This indicates a slightly below-average performance.
How do you calculate the percentage of students who scored below 72 when the mean is 60 and the standard deviation is 8?
-The z-score for 72 is calculated as: z = (72 - 60) / 8 = 1.5. From the z-table, the area for z = 1.5 is approximately 0.9332, meaning 93.32% of students scored below 72.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)