1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos
Summary
TLDREn este video, Jesús Grajeda explica cómo calcular la distancia entre dos puntos en un plano cartesiano utilizando la fórmula de distancia derivada del teorema de Pitágoras. A través de ejemplos prácticos, muestra cómo encontrar la distancia entre dos puntos dados o entre un punto y el origen. Además, se detiene a explicar el origen de la fórmula, destacando la importancia de restar las coordenadas X y Y de los puntos, elevarlas al cuadrado y luego sumarlas antes de tomar la raíz cuadrada. Es un tutorial claro y accesible para estudiantes de matemáticas.
Takeaways
- 😀 El objetivo del video es enseñar cómo calcular la distancia entre dos puntos en un plano cartesiano.
- 😀 Jesús Grajeda utiliza un enfoque visual para explicar la fórmula de distancia entre dos puntos, destacando la importancia de entender su origen.
- 😀 En el primer ejemplo, se calcula la distancia entre los puntos A(2, 3) y B(5, 7) usando el teorema de Pitágoras, resultando en una distancia de 5 unidades.
- 😀 Se utiliza un triángulo rectángulo para ilustrar cómo se derivan las distancias horizontales y verticales (3 y 4 unidades) entre los puntos A y B.
- 😀 El teorema de Pitágoras se aplica de forma práctica: la suma de los cuadrados de los catetos (3² + 4² = 25) y luego se calcula la raíz cuadrada para encontrar la distancia.
- 😀 La fórmula general para calcular la distancia entre dos puntos es: √[(x2 - x1)² + (y2 - y1)²].
- 😀 Jesús explica cómo se deriva la fórmula: restando las coordenadas correspondientes y elevándolas al cuadrado.
- 😀 En el segundo ejemplo, se aplica la fórmula para calcular la distancia entre los puntos J(2, -3) y K(5, 4), resultando en √58.
- 😀 El proceso de aplicación de la fórmula es el mismo: se restan las coordenadas, se elevan al cuadrado y luego se suman.
- 😀 En el tercer ejemplo, la distancia entre el punto P(6, 8) y el origen (0, 0) se calcula, resultando en 10 unidades.
- 😀 Jesús enfatiza que, al utilizar la fórmula, el orden de los puntos (X1, Y1) y (X2, Y2) no afecta el resultado, ya que las diferencias se elevan al cuadrado.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo principal del video es enseñar cómo determinar la distancia entre dos puntos en un plano cartesiano y explicar de dónde proviene la fórmula utilizada.
¿Qué fórmula se utiliza para calcular la distancia entre dos puntos?
-Se utiliza la fórmula de distancia: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
¿Cómo se obtiene la fórmula de distancia entre dos puntos?
-La fórmula se obtiene aplicando el teorema de Pitágoras, considerando que la distancia es la hipotenusa de un triángulo rectángulo formado por las diferencias en las coordenadas x e y de los puntos.
¿Cuál es la importancia de representar los puntos en un plano antes de aplicar la fórmula?
-Representar los puntos en un plano ayuda a visualizar el triángulo rectángulo y entender cómo se calculan los catetos, lo cual es fundamental para aplicar el teorema de Pitágoras correctamente.
¿Qué significa el valor de 3 y 4 en el primer ejemplo resuelto?
-En el primer ejemplo, los valores de 3 y 4 representan la diferencia en las coordenadas x e y entre los puntos A y B, respectivamente, que se usan como los catetos del triángulo rectángulo.
¿Por qué se toma solo el valor positivo al calcular la distancia?
-Se toma solo el valor positivo porque la distancia no puede ser negativa; la raíz cuadrada de un número negativo no tiene sentido en este contexto.
¿Cómo se aplicó la fórmula en el segundo ejemplo?
-En el segundo ejemplo, se sustituyeron las coordenadas de los puntos J y K en la fórmula de distancia y se resolvieron las operaciones: \( d = \sqrt{(5 - 2)^2 + (4 - (-3))^2} = \sqrt{3^2 + 7^2} = \sqrt{58} \).
¿Qué pasos se siguieron para resolver el tercer ejemplo?
-Para el tercer ejemplo, se calculó la distancia desde el punto C(6, 8) hasta el origen (0, 0). Se aplicó la fórmula \( d = \sqrt{(0 - 6)^2 + (0 - 8)^2} \), resultando en \( d = \sqrt{36 + 64} = \sqrt{100} = 10 \).
¿Cuál es la diferencia entre los valores de X1, Y1 y X2, Y2?
-Los valores de X1, Y1 y X2, Y2 representan las coordenadas de los dos puntos entre los que se calcula la distancia. Pueden intercambiarse sin que la distancia cambie, ya que la resta de dos números al cuadrado es igual independientemente del orden.
¿Por qué es importante entender de dónde proviene la fórmula de distancia?
-Es importante para comprender cómo se deriva y aplicar correctamente la fórmula en diferentes situaciones, mejorando así la comprensión de conceptos matemáticos y su aplicación práctica.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Distancia Entre Dos Puntos En El Plano Cartesiano

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia entre dos puntos | Demostración de la fórmula

DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO

Distancia entre dos puntos ejemplo 3 método gráfico
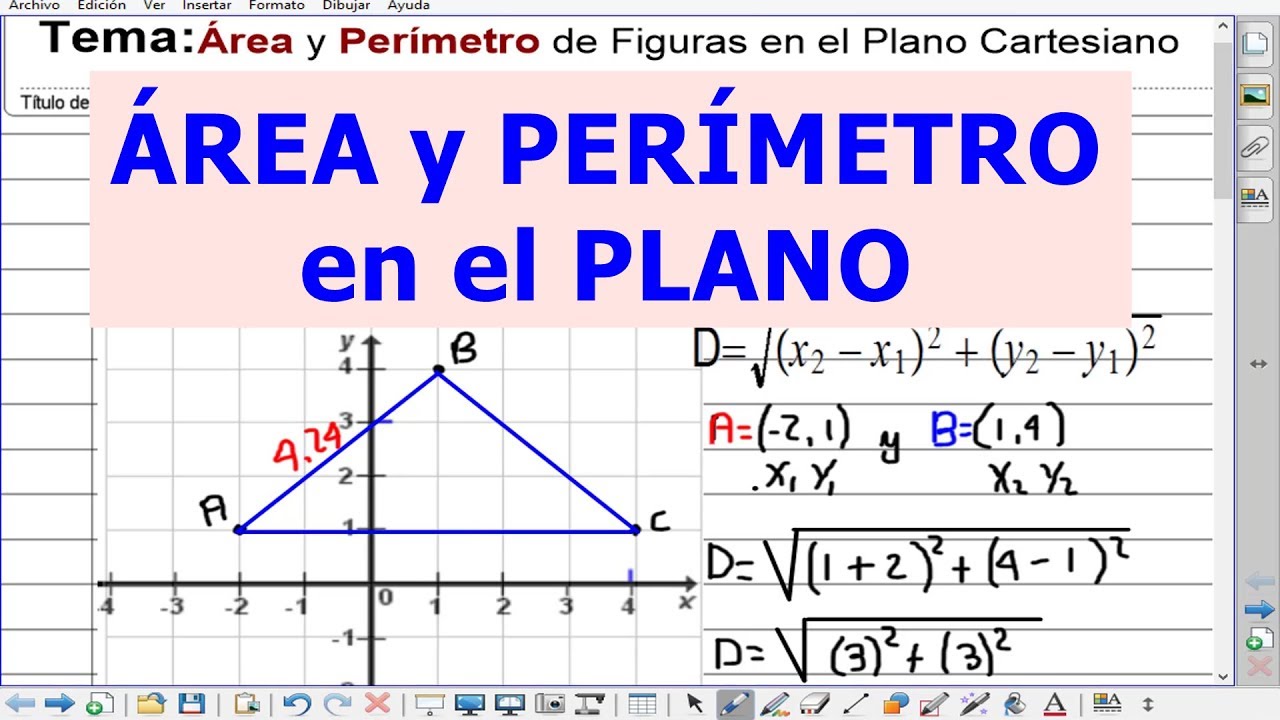
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)