DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO
Summary
TLDREn este video, se presenta la demostración de la fórmula para calcular la distancia entre dos puntos en un plano cartesiano. Se comienza identificando dos puntos, P1 y P2, con sus respectivas coordenadas (x1, y1) y (x2, y2). Se utiliza el teorema de Pitágoras para relacionar la hipotenusa del triángulo rectángulo formado por estos puntos con sus catetos, resultando en la fórmula d = √((x2 - x1)² + (y2 - y1)²). Se aplica el ejemplo práctico de encontrar la distancia entre los puntos A(-3, 1) y B(1, -2), obteniendo un resultado de 5 unidades. Finalmente, se verifica gráficamente la distancia obtenida, confirmando la precisión del método analítico.
Takeaways
- 📚 La demostración explica cómo calcular la distancia entre dos puntos en un plano cartesiano.
- 📐 Se comienza considerando dos puntos cualesquiera, P1 y P2, con sus respectivas coordenadas (x1, y1) y (x2, y2).
- 🔍 Se utiliza un triángulo rectángulo para determinar las longitudes de los catetos, que son las diferencias entre las abscisas y ordenadas de los puntos P1 y P2.
- 📈 El teorema de Pitágoras se aplica para relacionar la longitud de la hipotenusa (la distancia entre P1 y P2) con las longitudes de los catetos.
- 🧩 Se resuelve la ecuación de Pitágoras para encontrar la longitud de la hipotenusa, que representa la distancia entre los puntos.
- 🔢 La fórmula resultante para la distancia es \( \sqrt{(x2 - x1)^2 + (y2 - y1)^2} \).
- 📝 Se proporciona un ejemplo práctico para aplicar la fórmula, donde se calcula la distancia entre los puntos A(-3, 1) y B(1, -2).
- 📊 El resultado del ejemplo muestra que la distancia entre A y B es de 5 unidades.
- 📏 Se verifica la distancia analítica con una escuadra gráfica para confirmar la precisión del cálculo.
- 🖼️ La demostración incluye una representación visual de los puntos en el plano cartesiano y el segmento entre ellos.
- 🎓 El script es una lección completa que combina teoría y práctica para entender cómo medir distancias en un plano cartesiano.
Q & A
¿Qué es la fórmula para determinar la distancia entre dos puntos en el plano cartesiano?
-La fórmula para determinar la distancia entre dos puntos en el plano cartesiano es la raíz cuadrada de la suma del cuadrado de la diferencia de las abscisas y el cuadrado de la diferencia de las ordenadas de los puntos.
¿Cómo se llaman los puntos considerados en la demostración de la fórmula?
-Los puntos considerados en la demostración son P1 y P2, donde P1 tiene coordenadas (x1, y1) y P2 tiene coordenadas (x2, y2).
¿Qué es un cateto en un triángulo rectángulo?
-Un cateto en un triángulo rectángulo es uno de los lados que forman el ángulo recto, y su longitud es la diferencia entre las coordenadas de los puntos que lo forman.
¿Cuál es el teorema aplicado para relacionar las longitudes de los lados de un triángulo rectángulo?
-El teorema aplicado es el teorema de Pitágoras, que establece que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos.
¿Cómo se determina la longitud de la hipotenusa en un triángulo rectángulo?
-La longitud de la hipotenusa se determina a través de la raíz cuadrada de la suma de los cuadrados de las longitudes de los catetos.
¿Por qué las distancias siempre deben ser cantidades positivas?
-Las distancias siempre deben ser positivas porque no es posible medir una distancia negativa en el espacio; la longitud de un segmento no puede ser menos que cero.
¿Cómo se aplicó la fórmula para encontrar la distancia entre los puntos A y B en el ejemplo dado?
-Se aplicó la fórmula sustituyendo las coordenadas de los puntos A y B, calculando la diferencia de las abscisas y las ordenadas, elevándolas al cuadrado y sumándolas, y finalmente tomando la raíz cuadrada del resultado.
¿Cuál es la distancia entre los puntos A y B según el ejemplo proporcionado?
-La distancia entre los puntos A y B, según las coordenadas proporcionadas en el ejemplo, es de 5 unidades.
¿Cómo se puede verificar la distancia analíticamente determinada gráficamente?
-Se puede verificar gráficamente marcando los puntos en el plano cartesiano y mediendo la longitud del segmento que los une utilizando una escuadra o herramienta similar.
¿Qué herramienta se utiliza para verificar la distancia en el plano cartesiano?
-Se utiliza una escuadra para verificar la distancia en el plano cartesiano, asegurándose de que la medida corresponda a la distancia analíticamente calculada.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos
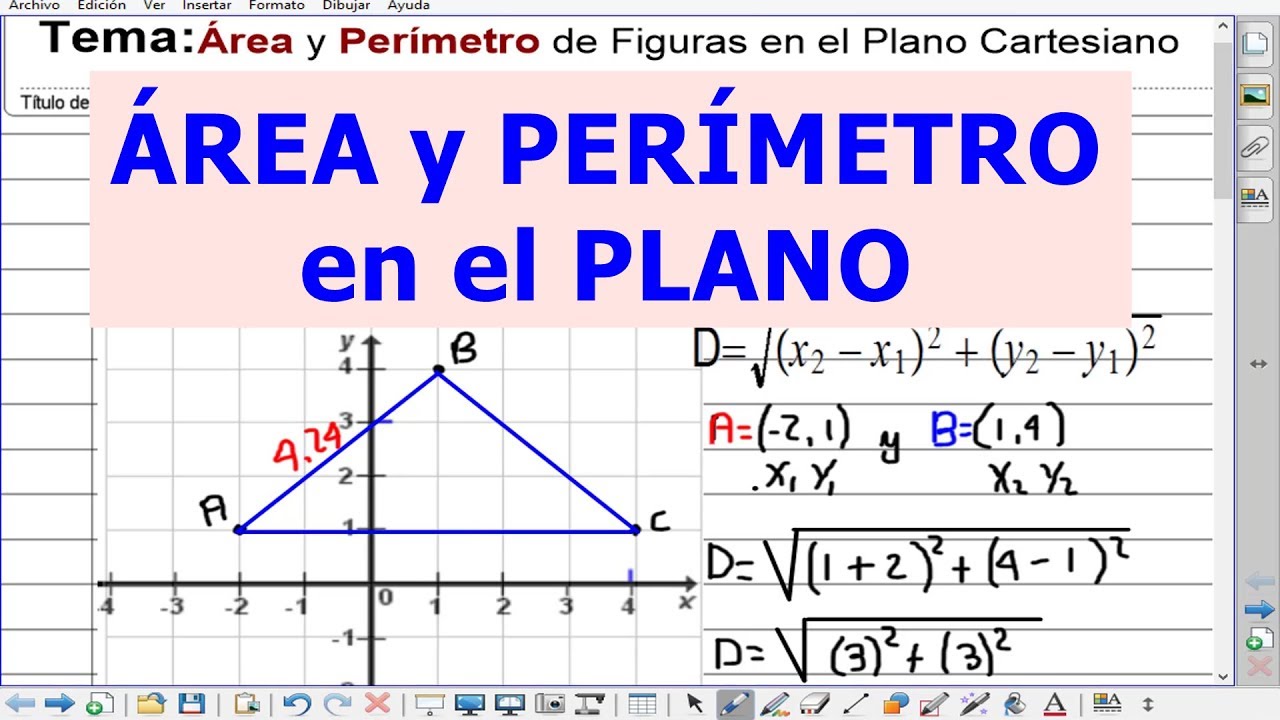
Área y Perímetro de Figuras en el Plano Cartesiano.

Distancia entre dos puntos Ejemplo 1

Distancia Entre Dos Puntos En El Plano Cartesiano

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia entre dos puntos | Demostración de la fórmula
5.0 / 5 (0 votes)
