0625 Distribución geométrica
Summary
TLDREste video explica la distribución geométrica y su aplicación en probabilidad. A través de ejemplos detallados, se describe cómo calcular la función de probabilidad, esperanza y varianza de una variable aleatoria con distribución geométrica. Se muestra cómo la probabilidad de obtener un éxito en ensayos independientes Bernoulli sigue una progresión geométrica, y se utiliza un ejemplo práctico sobre un juego de lotería para ilustrar el cálculo de la esperanza de participaciones necesarias hasta ganar. Es una introducción completa a la distribución geométrica y sus propiedades matemáticas.
Please replace the link and try again.
Q & A
¿Qué describe la variable aleatoria X en la distribución geométrica?
-La variable aleatoria X representa el número de fracasos antes de obtener el primer éxito en una sucesión de ensayos de Bernoulli independientes.
¿Cómo se calcula la función de probabilidad de la distribución geométrica?
-La función de probabilidad de la distribución geométrica está dada por la expresión: P(X = x) = p * (1 - p)^x, donde p es la probabilidad de éxito en cada ensayo y x es el número de fracasos antes del primer éxito.
¿Cuál es la forma de la gráfica de la función de probabilidad de una distribución geométrica?
-La gráfica de la función de probabilidad tiene una forma decreciente, alcanzando su valor máximo en x = 0, y luego disminuyendo a medida que x aumenta.
¿Qué es una suma geométrica y por qué es importante en la distribución geométrica?
-Una suma geométrica es una suma de términos de la forma a^n, con n variando en un intervalo. En la distribución geométrica, las sumas geométricas se utilizan para calcular probabilidades y momentos como la esperanza y la varianza.
¿Qué significa que la función de distribución F(x) sea una función de probabilidad válida?
-Significa que la suma de las probabilidades de todos los posibles valores de la variable aleatoria X debe ser igual a 1, lo cual se verifica mediante los cálculos presentados en el script.
¿Cómo se calcula la esperanza de una variable aleatoria con distribución geométrica?
-La esperanza de una variable aleatoria X con distribución geométrica es igual a (1 - p) / p, donde p es la probabilidad de éxito en cada ensayo.
¿Cuál es la fórmula para la varianza de una distribución geométrica?
-La varianza de una distribución geométrica es (1 - p) / p^2, donde p es la probabilidad de éxito en cada ensayo.
¿Cómo se obtiene el segundo momento de la distribución geométrica?
-El segundo momento se obtiene a partir de la suma de los términos x^2 multiplicados por la función de probabilidad. Luego se calcula como la suma de dos términos, uno relacionado con la esperanza y otro con un término geométrico.
¿Cómo se aplica la distribución geométrica en un ejemplo práctico de la lotería?
-En el ejemplo de la lotería, se define la variable X como el número de participaciones sin premio antes de ganar. Usando la fórmula de la esperanza de la distribución geométrica, se calcula que en promedio, una persona debe participar más de 17,000 años para ganar la lotería, con una probabilidad de éxito de 1 entre un millón.
¿Qué son las funciones generadoras de probabilidad y de momentos en la distribución geométrica?
-La función generadora de probabilidad y la función generadora de momentos son herramientas matemáticas que permiten calcular la probabilidad y los momentos (como la esperanza) de una distribución. En la distribución geométrica, estas funciones están dadas por las expresiones (1 - (1 - p)t) / (1 - p) y (1 - (1 - p)e^t) / (1 - p), respectivamente.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

DISTRIBUCIÓN t DE STUDENT | | UPV

Distribución binomial | Ejercicios resueltos | Introducción

Distribución Hipergeométrica
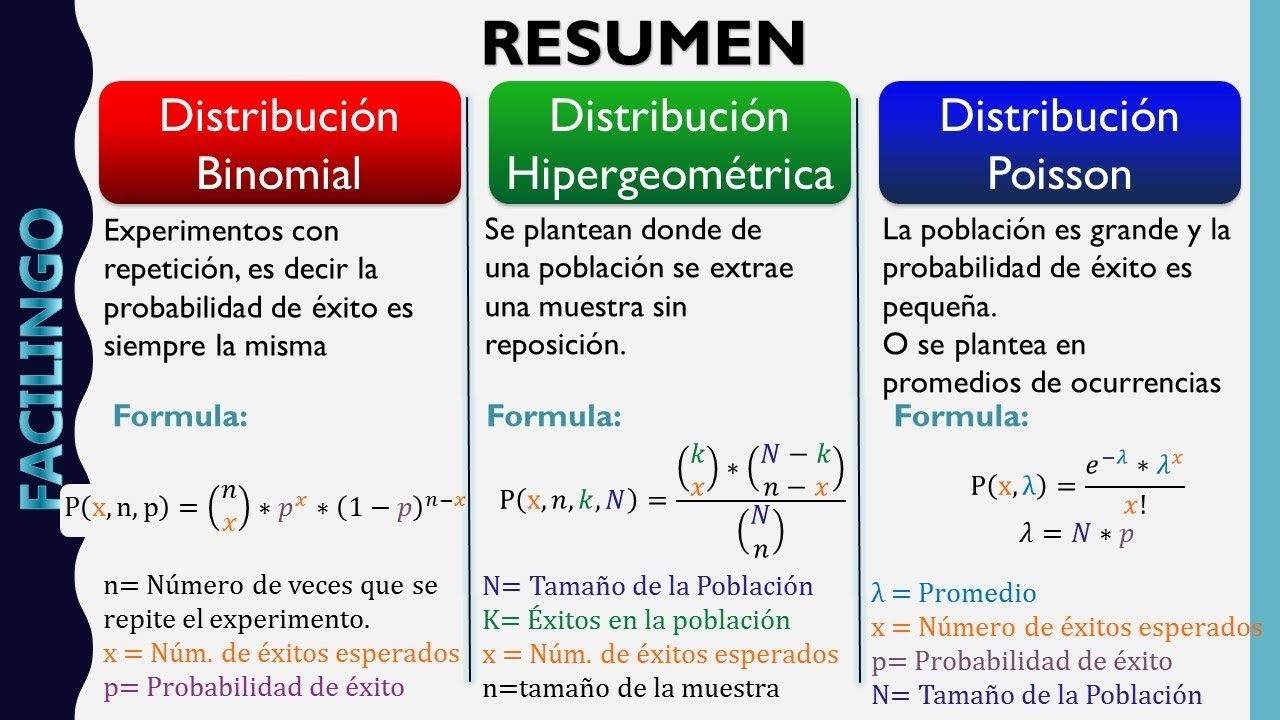
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

02 Distribución binomial. Función de probabilidad

Ejemplo Distribución de Poisson (Probabilidad, Esperanza Matemática y Varianza)

Uso de la tabla t-student
5.0 / 5 (0 votes)