Distribución Hipergeométrica
Summary
TLDREn este video se explica la distribución de probabilidad hipergeométrica, que se utiliza en situaciones donde se selecciona una muestra sin reemplazo de una población finita. A diferencia de la distribución binomial, la probabilidad no se mantiene constante porque depende de los resultados previos. Se presenta la fórmula y ejemplos prácticos, como el cálculo de la probabilidad de seleccionar abanicos defectuosos y celulares dañados en muestras aleatorias. El video demuestra cómo aplicar la fórmula paso a paso, proporcionando una comprensión clara de este tipo de distribución y su utilidad en diversas situaciones estadísticas.
Takeaways
- 😀 La distribución de probabilidad hipergeométrica se utiliza cuando el tamaño de la población es pequeño y se selecciona una muestra sin reemplazo.
- 😀 A diferencia de la distribución binomial, la probabilidad en la hipergeométrica cambia con cada experimento debido a la selección sin reemplazo.
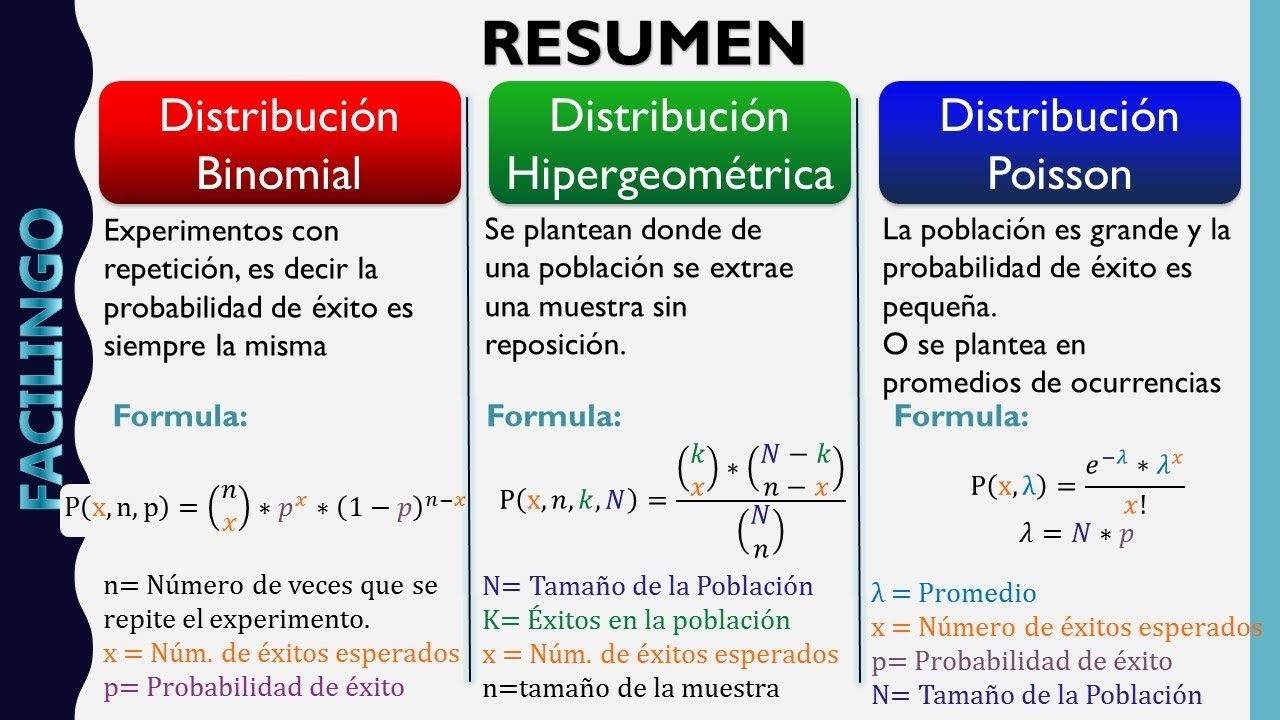
- 😀 La fórmula de la distribución hipergeométrica involucra el tamaño de la población (N), el tamaño de la muestra (n), los éxitos en la población (K) y los éxitos en la muestra (X).
- 😀 Un ejemplo de aplicación de la distribución hipergeométrica es cuando se produce un nuevo tipo de abanicos defectuosos en una empresa.
- 😀 En el ejemplo de los abanicos, se tiene una población de 12 abanicos, de los cuales 3 son defectuosos. Se selecciona una muestra de 4, y se calcula la probabilidad de que 2 sean defectuosos.
- 😀 Para calcular la probabilidad en el ejemplo de los abanicos, se usan combinaciones para calcular las posibles configuraciones de éxitos y fracasos en la muestra.
- 😀 En el ejemplo de la caja con celulares, se calcula la probabilidad de que un celular defectuoso sea seleccionado de una muestra de 5, dada una población de 10 celulares y 3 defectuosos.
- 😀 La probabilidad de que un celular defectuoso sea seleccionado en el ejemplo de la caja es aproximadamente 41.66%.
- 😀 La distribución hipergeométrica es útil para problemas donde se seleccionan muestras sin reemplazo y se necesitan calcular probabilidades en función de éxitos y fracasos.
- 😀 La clave para usar correctamente la distribución hipergeométrica es identificar correctamente los parámetros de la población, la muestra y los éxitos, luego aplicar la fórmula de combinaciones.
Q & A
¿Qué es la distribución de probabilidad hipergeométrica?
-La distribución de probabilidad hipergeométrica se utiliza cuando el tamaño de la población es pequeño, la muestra se selecciona sin reemplazo y la probabilidad de éxito cambia dependiendo de los resultados anteriores del experimento.
¿Cuál es la principal diferencia entre la distribución binomial y la hipergeométrica?
-La principal diferencia es que en la distribución binomial la probabilidad de éxito se mantiene constante, mientras que en la distribución hipergeométrica cambia dependiendo de los resultados previos debido a la muestra sin reemplazo.
¿En qué situaciones se aplica la distribución hipergeométrica?
-Se aplica cuando el tamaño de la población es finito, se selecciona una muestra sin reemplazo y existe una característica en la muestra que también está presente en la población.
¿Qué representa cada variable en la fórmula de la distribución hipergeométrica?
-En la fórmula, N (mayúscula) representa el tamaño de la población, n (minúscula) es el tamaño de la muestra, K es la cantidad de éxitos en la población y x es la cantidad de éxitos en la muestra.
¿Qué es un ejemplo de aplicación de la distribución hipergeométrica en la vida real?
-Un ejemplo es en una empresa que produce abanicos, donde, si de los primeros 12 abanicos producidos, 3 fueron defectuosos, la probabilidad de que 2 defectuosos sean seleccionados al azar de una muestra de 4 se puede calcular usando la distribución hipergeométrica.
¿Cómo se calcula la probabilidad en un problema de distribución hipergeométrica?
-La probabilidad se calcula usando combinaciones en la fórmula, que involucra calcular la cantidad de formas en las que se pueden seleccionar los éxitos y fracasos en la muestra, y luego dividirlo por el total de formas posibles de seleccionar la muestra.
En el ejemplo de los abanicos, ¿cuál es la probabilidad de que dos abanicos defectuosos sean seleccionados de una muestra de cuatro?
-La probabilidad es de aproximadamente 21.81%.
En el segundo ejemplo de los celulares, ¿qué se está buscando calcular?
-Se está buscando calcular la probabilidad de que, al seleccionar 5 celulares al azar de una caja de 10, uno de ellos sea dañado, sabiendo que 3 de los 10 celulares son defectuosos.
¿Qué datos se necesitan para aplicar la fórmula de la distribución hipergeométrica en el segundo ejemplo de los celulares?
-Se necesitan el tamaño de la población (10 celulares), el tamaño de la muestra (5 celulares), la cantidad de éxitos en la población (3 celulares defectuosos) y la cantidad de éxitos que se espera en la muestra (1 celular defectuoso).
¿Cuál es la probabilidad de que uno de los celulares seleccionados al azar esté dañado, según el segundo ejemplo?
-La probabilidad es de aproximadamente 41.66%.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

tamaño de la muestra de una población finita

Tamaño de Muestra para Variables Cualitativas con Población Indefinida

Tamaño de Muestra para Variables Cuantitativas con Población Finita

Domina el Teorema del Límite Central: Qué es y por qué es tan Importante - Python

Pensamiento matemático I. Progresión 3. Equiprobabilidad
5.0 / 5 (0 votes)
