Ejemplo Distribución de Poisson (Probabilidad, Esperanza Matemática y Varianza)
Summary
TLDREste video explica la distribución de Poisson, enfocándose en cómo calcular probabilidades y estadísticas asociadas. Se presentan ejemplos prácticos, como el cálculo de la probabilidad de desbordes anuales en una determinada área, utilizando la fórmula de Poisson. Se cubren casos específicos como encontrar la probabilidad de eventos exactos, a lo sumo o al menos un número determinado de ocurrencias, así como la esperanza matemática y la varianza. A lo largo del video se detallan los pasos para aplicar correctamente la distribución de Poisson y se ofrece una explicación clara de cada concepto involucrado.
Takeaways
- 😀 La distribución de Poisson se utiliza para modelar la probabilidad de que ocurran un número determinado de eventos dentro de un intervalo de tiempo fijo.
- 😀 El parámetro lambda (λ) en la distribución de Poisson representa el promedio de ocurrencias de un evento en un periodo específico.
- 😀 La fórmula básica de la distribución de Poisson es: P(X = x) = (λ^x * e^(-λ)) / x!, donde 'x' es el número de éxitos y 'λ' es el promedio de ocurrencias.
- 😀 La distribución de Poisson es útil cuando la probabilidad de que un evento ocurra en un intervalo es pequeña, pero la población es grande.
- 😀 En ejercicios prácticos, la probabilidad de un número específico de eventos se calcula sustituyendo 'x' en la fórmula de Poisson.
- 😀 Si se desea calcular la probabilidad de que ocurran hasta 'n' eventos, se suman las probabilidades de cada número de eventos hasta 'n'.
- 😀 La probabilidad de que ocurran 'a lo sumo' 'n' eventos implica calcular las probabilidades para 0, 1, ..., n y sumarlas.
- 😀 En el caso de que se necesite calcular la probabilidad de que ocurran 'al menos' 'n' eventos, se usa la ley del complemento: P(X ≥ n) = 1 - P(X < n).
- 😀 Para calcular la esperanza matemática de una distribución de Poisson, simplemente se utiliza el valor de lambda (λ).
- 😀 La varianza de una distribución de Poisson también es igual a λ, lo que significa que la varianza y la esperanza matemática son iguales.
- 😀 La distribución de Poisson se aplica en situaciones prácticas como el cálculo de desbordes de ríos, accidentes o cualquier otro evento que ocurra al azar con una tasa constante.
Q & A
¿Qué es la distribución de Poisson?
-La distribución de Poisson es un modelo probabilístico que describe la ocurrencia de eventos en intervalos de tiempo o espacio determinados, bajo la condición de que los eventos son independientes entre sí y ocurren con una tasa constante promedio.
¿Cuál es la fórmula general para calcular la probabilidad en una distribución de Poisson?
-La fórmula general es: P(X = x) = (λ^x * e^(-λ)) / x!, donde λ es la tasa promedio de ocurrencias, e es el número de Euler (aproximadamente 2.71828), y x es el número de eventos o éxitos esperados.
¿Qué significa el parámetro λ (lambda) en una distribución de Poisson?
-El parámetro λ (lambda) representa la tasa promedio de ocurrencias o eventos en un intervalo de tiempo o espacio determinado. Es un valor que debe ser especificado en el problema y se utiliza para calcular las probabilidades asociadas con la distribución.
¿Cómo se calcula la probabilidad de que ocurran exactamente 3 desbordes en un año?
-Para calcular la probabilidad de que ocurran exactamente 3 desbordes, se utiliza la fórmula de Poisson con λ = 6 (promedio de desbordes al año) y x = 3. La fórmula sería: P(X = 3) = (6^3 * e^(-6)) / 3!.
¿Qué representa la variable 'x' en la distribución de Poisson?
-En la distribución de Poisson, 'x' representa el número de eventos o éxitos esperados en un intervalo de tiempo o espacio. Por ejemplo, puede ser el número de accidentes, desbordes u otros eventos de interés.
¿Cómo se interpreta la probabilidad de que ocurran a lo sumo 2 desbordes en un año?
-La probabilidad de que ocurran a lo sumo 2 desbordes (es decir, 0, 1 o 2 desbordes) se calcula sumando las probabilidades de que x sea igual a 0, 1 o 2, es decir, P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2).
¿Qué significa 'al menos 2 desbordes' y cómo se calcula su probabilidad?
-La probabilidad de que ocurran 'al menos 2 desbordes' se calcula como el complemento de la probabilidad de que ocurran menos de 2 desbordes. Es decir, P(X ≥ 2) = 1 - P(X < 2). Para calcular P(X < 2), sumamos las probabilidades de que x sea 0 o 1.
¿Cómo se calcula la esperanza matemática de una distribución de Poisson?
-La esperanza matemática (o media) de una distribución de Poisson es igual al parámetro λ. Es decir, E(X) = λ. En el ejemplo dado, si λ = 6, entonces la esperanza matemática es 6.
¿Cuál es la fórmula para calcular la varianza de una distribución de Poisson?
-La varianza de una distribución de Poisson es igual a su parámetro λ. Es decir, Var(X) = λ. En el ejemplo del ejercicio, si λ = 6, la varianza también es 6.
¿Qué precauciones deben tomarse al usar calculadoras para resolver ejercicios de Poisson?
-Es importante tener cuidado con la notación y la forma en que se ingresan los valores en la calculadora. Algunos cálculos pueden requerir el uso de paréntesis para exponentes o fracciones, y el valor de e debe ser ingresado correctamente para obtener resultados precisos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Distribución de Poisson | Ejercicios resueltos | Intro
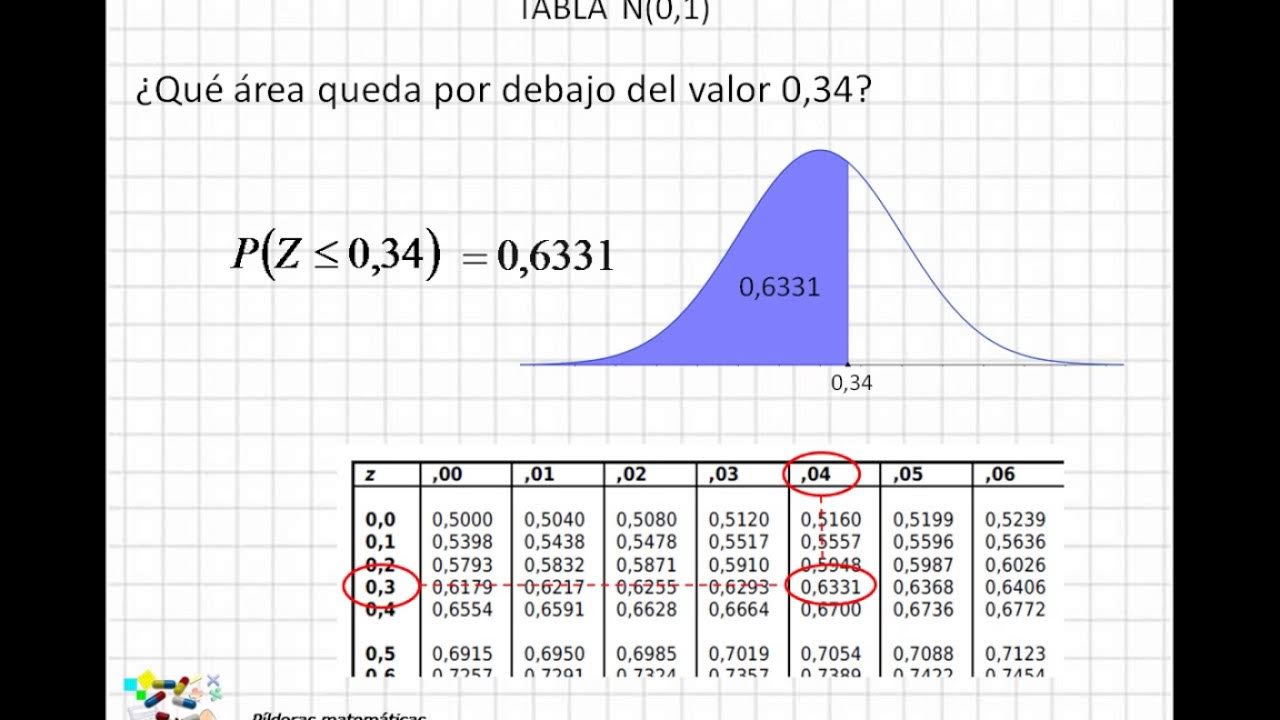
04 Cómo usar la tabla de distribución normal

UCC Stats Final Review

15 Variable aleatoria y función de distribución acumulativa
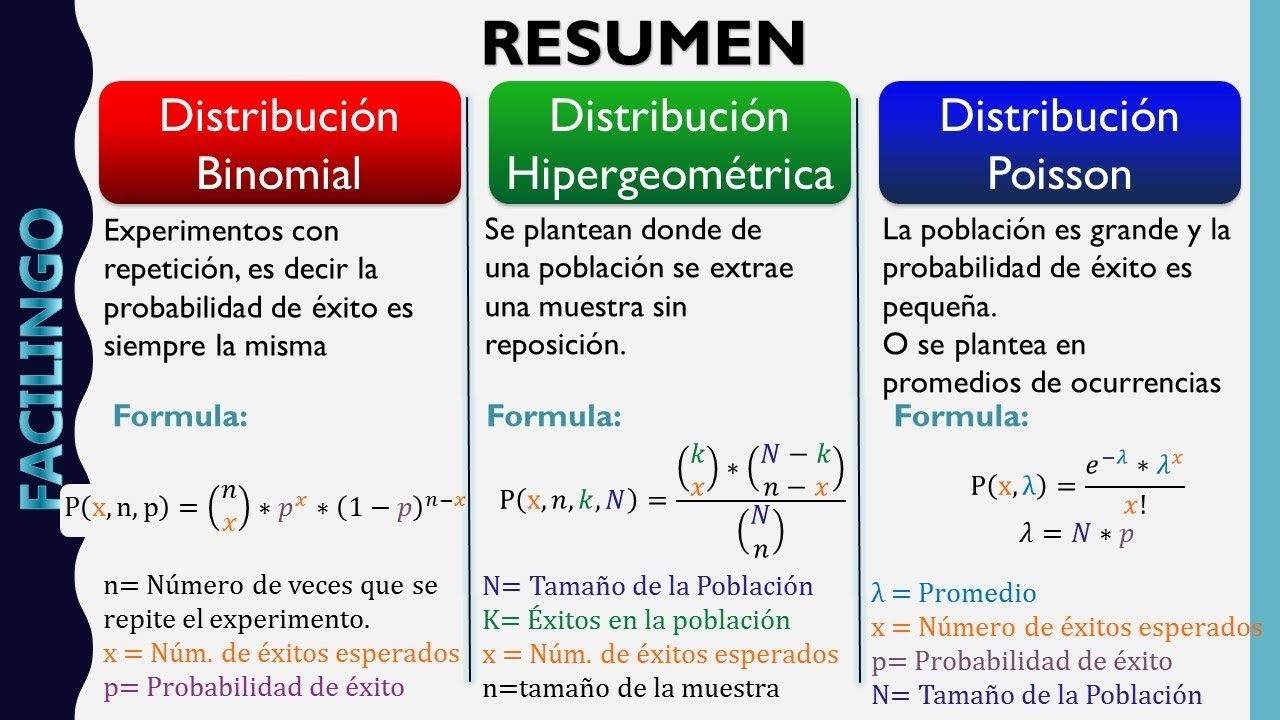
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

¿Cuál es la probabilidad aseguradora pague 4 indemnizaciones en 1 año? Poisson en Excel
5.0 / 5 (0 votes)
