Notasi dan Operasi Vektor
Summary
TLDRThis educational video provides an introduction to vectors, focusing on their notation, magnitude, and key operations. Viewers learn about vector basics, including how to represent vectors, calculate their magnitude, and understand unit vectors. The video covers essential vector operations such as vector addition, scalar multiplication, and both dot and cross products. With practical examples and clear explanations, it serves as a foundational lesson for anyone looking to grasp the core concepts of vectors in mathematics. The tutorial concludes with a preview of more advanced topics in vector operations.
Takeaways
- 😀 A vector is a quantity that has both magnitude and direction, and it is commonly represented as a matrix or a set of components along different axes.
- 😀 The magnitude of a vector is the square root of the sum of the squares of its components, and it represents the length of the vector.
- 😀 A unit vector is a vector with a magnitude of 1. It's often used to indicate direction without altering the vector's length.
- 😀 Vector addition involves adding the corresponding components of two vectors, resulting in a new vector.
- 😀 Scalar multiplication involves multiplying each component of a vector by a scalar, which affects the vector's magnitude but not its direction unless the scalar is negative.
- 😀 The dot product of two vectors results in a scalar and is computed by multiplying corresponding components and summing the results.
- 😀 The cross product results in a new vector that is perpendicular to both original vectors, and it's defined only in three-dimensional space.
- 😀 In vector operations, vectors can be added or subtracted by performing component-wise addition or subtraction.
- 😀 A scalar can scale a vector, changing its magnitude without affecting its direction unless the scalar is negative.
- 😀 The difference between dot and cross products: the dot product results in a scalar, while the cross product results in a new vector.
- 😀 Visualizing vector operations, such as vector addition and scalar multiplication, can help in understanding how they work geometrically, such as through vector diagrams.
Q & A
What is a vector and how is it represented?
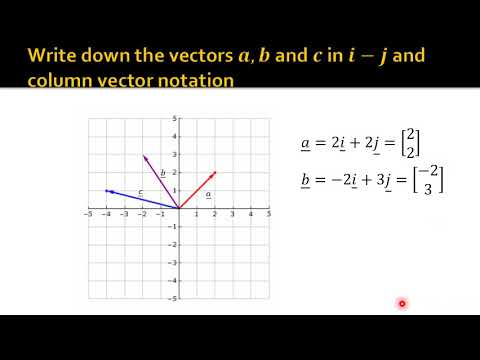
-A vector is a quantity that has both magnitude and direction. It is often represented in matrix form, such as a 3x1 matrix. For example, a vector can be written as: [C1, C2, C3], where C1, C2, and C3 are the vector's components along the i, j, and k directions, respectively.
How is the magnitude of a vector calculated?
-The magnitude of a vector is calculated by taking the square root of the sum of the squares of its components. For example, for the vector [C1, C2, C3], the magnitude is: √(C1² + C2² + C3²).
What is a unit vector and how do you determine if a vector is a unit vector?
-A unit vector is a vector with a magnitude of 1. To determine if a vector is a unit vector, calculate its magnitude. If the magnitude is 1, the vector is a unit vector. For example, the vector [1, 2, 3] is not a unit vector because its magnitude is √14, which is not equal to 1.
What does the notation of a vector typically look like?
-The notation of a vector typically looks like a column matrix or list, such as: [C1, C2, C3]. It can also be written in a more descriptive form, for instance, as a combination of unit vectors: C1*i + C2*j + C3*k, where i, j, and k are unit vectors in the x, y, and z directions, respectively.
How is vector addition performed?
-Vector addition is performed by adding the corresponding components of the two vectors. For example, if you have vectors [u1, u2, u3] and [v1, v2, v3], their sum is: [u1 + v1, u2 + v2, u3 + v3].
What is scalar multiplication and how is it done?
-Scalar multiplication involves multiplying each component of a vector by a scalar. For instance, if a vector [1, 2, 3] is multiplied by a scalar 3, the result is [3, 6, 9]. The direction of the vector remains the same if the scalar is positive, but it reverses if the scalar is negative.
What is the difference between the dot product and the cross product of two vectors?
-The dot product (or scalar product) of two vectors results in a scalar value and is calculated by multiplying corresponding components and summing them. The cross product (or vector product) results in another vector that is perpendicular to both of the original vectors, and it is only defined in 3-dimensional space.
When is the dot product of two vectors equal to zero?
-The dot product of two vectors is equal to zero when the vectors are perpendicular to each other. This occurs because the cosine of the angle between them is zero, which is part of the formula for the dot product.
What is the result of the cross product of two vectors?
-The result of the cross product is a new vector that is perpendicular to both of the original vectors. This vector is determined using the determinant of a matrix formed by the components of the two vectors.
How do you perform vector subtraction?
-Vector subtraction is done by subtracting the corresponding components of two vectors. For example, if you have vectors [u1, u2, u3] and [v1, v2, v3], their difference is: [u1 - v1, u2 - v2, u3 - v3].
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)