Vectors Physics Class 11th
Summary
TLDRThis video provides a comprehensive and easy-to-understand introduction to vectors. It covers the basic concepts of scalars and vectors, highlighting their differences and real-world applications. The video delves into vector notation, types of vectors (such as position and displacement vectors), and important mathematical operations like addition, subtraction, and scalar multiplication. Key vector properties and terms like unit vectors, zero vectors, and co-initial vectors are also explained. The content is designed to help viewers grasp the fundamentals of vector algebra with simple examples and clear visuals, making it ideal for beginners in physics and mathematics.
Takeaways
- 😀 Vectors are physical quantities that have both magnitude and direction, while scalars only have magnitude (e.g., mass, distance, and time).
- 😀 Vectors can be represented in multiple ways, such as with an arrow on top or in bold to indicate their magnitude and direction.
- 😀 Scalar quantities can be added algebraically, but vector addition requires special laws due to their directional nature.
- 😀 A position vector describes the location of an object relative to a reference point (origin), and can be calculated using Pythagoras' theorem.
- 😀 Displacement vectors represent the change in position from one point to another and do not consider the path taken, only the start and end points.
- 😀 Polar vectors have both a starting point and a direction (e.g., force, displacement), while axial vectors represent rotational effects (e.g., torque, angular velocity).
- 😀 Two vectors are equal if they have the same magnitude and direction, while the negative of a vector has the same magnitude but the opposite direction.
- 😀 The modulus of a vector refers to its magnitude, and a unit vector has a magnitude of 1 and points in the direction of the original vector.
- 😀 Free vectors do not have a fixed initial point (e.g., force vectors), while fixed vectors have a specific origin (e.g., position vectors).
- 😀 The zero vector has zero magnitude and no specific direction, often used in calculations as the additive identity in vector arithmetic.
- 😀 Scalar multiplication of a vector results in a new vector with the same direction (if the scalar is positive) or opposite direction (if the scalar is negative), with the magnitude scaled accordingly.
Q & A
What is the difference between scalar and vector quantities?
-Scalar quantities have only magnitude, such as mass, time, or temperature. Vector quantities, on the other hand, have both magnitude and direction, like force, velocity, and displacement.
How do we represent vectors in notation?
-Vectors are usually represented by an arrow above the letter or in bold. For example, force can be written as F with an arrow (→F) or as bold F. To represent the magnitude of a vector, we drop the arrow or write it without bold formatting.
Can you add two vectors as you would scalars?
-No, vectors cannot be added simply like scalars. While scalars are added according to basic algebraic rules, vectors require special vector addition, considering both their magnitude and direction.
What is a position vector and how is it different from a displacement vector?
-A position vector describes the location of an object in space relative to a reference point or origin. A displacement vector, however, represents the change in position of an object, showing the shortest path from the initial to the final point.
What is the significance of the zero vector?
-The zero vector has zero magnitude and no specific direction. It is often used in mathematical operations, such as when subtracting two equal vectors, resulting in a zero vector. It is also crucial in representing the position of stationary objects or objects at the origin.
What are polar vectors and axial vectors?
-Polar vectors have a point of application and include quantities like displacement, velocity, and force. Axial vectors, on the other hand, represent rotational effects and act along an axis of rotation, like angular momentum or torque.
How do you calculate the magnitude of a vector from its components?
-The magnitude of a vector can be calculated using the Pythagorean theorem. For example, for a position vector with components (3, 4), the magnitude would be the square root of (3² + 4²), which equals 5 units.
What happens when you multiply a vector by a scalar?
-When you multiply a vector by a scalar, the magnitude of the vector changes by the scalar value, while the direction remains the same if the scalar is positive. If the scalar is negative, the direction of the vector is reversed.
What is the difference between co-initial and co-terminus vectors?
-Co-initial vectors share the same starting point, or tail, but may point in different directions. Co-terminus vectors share the same ending point, or head, even if their starting points differ.
What is a unit vector and how is it related to a given vector?
-A unit vector has a magnitude of one and points in the same direction as the given vector. It can be obtained by dividing a vector by its magnitude. Unit vectors are often represented with a hat symbol (e.g., î, ĵ).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Vektor pada dimensi tiga | Vektor dimensi 3

Notasi dan Operasi Vektor

Kaidah Pencacahan, aturan penjumlahan, aturan perkalian, filling slot mudah dan gampang dipahami.
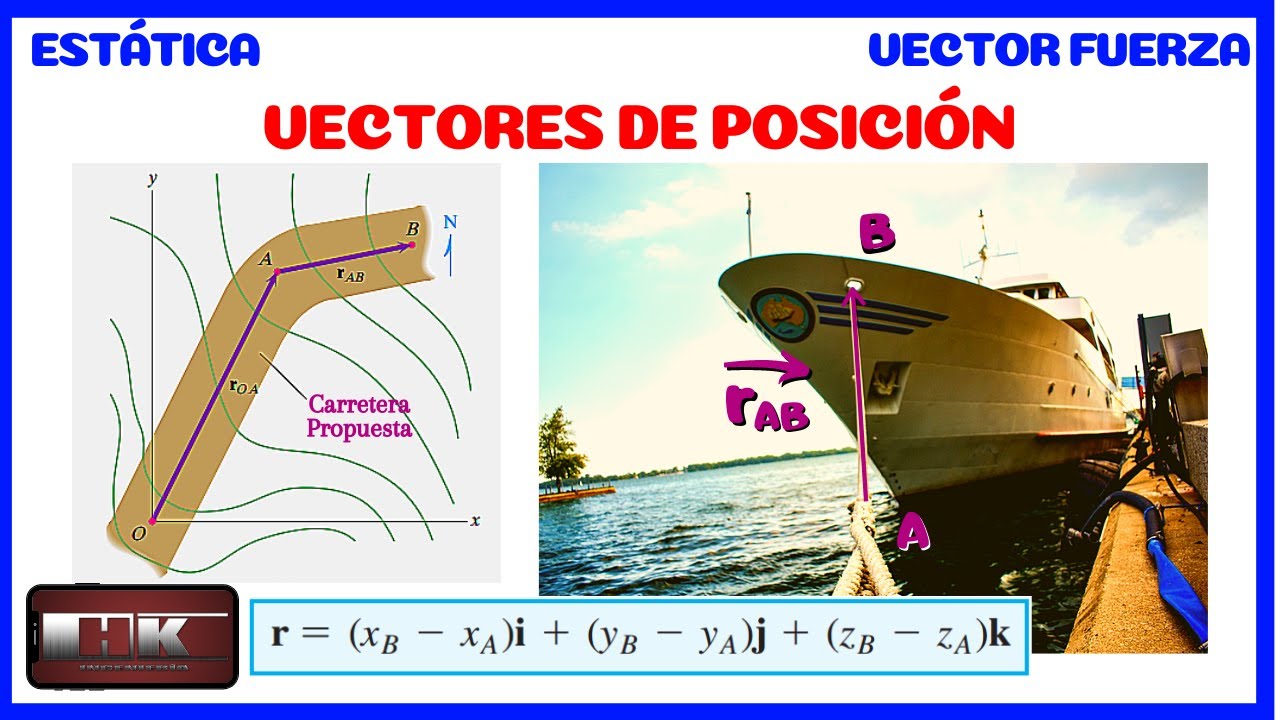
VECTORES DE POSICION. TEORÍA Y CONCEPTOS DE ESTÁTICA 👨🏫

Vektor Matematika Kelas 10 • Part 1: Definisi Vektor & Cara Menyatakan Vektor

Everything You Need to Know About VECTORS
5.0 / 5 (0 votes)