Everything You Need to Know About VECTORS

Summary

This video explains the fundamentals of vectors and coordinate systems in a two-dimensional space. It starts with an introduction to coordinate systems, demonstrating how to assign coordinates to points. The video then dives into vectors, exploring their components, notation, and operations like scalar multiplication and vector addition. It also covers vector length, the concept of unit vectors, and two types of vector multiplication: the dot product and cross product. Throughout, visual aids and simple explanations are used to help viewers understand these mathematical concepts, making complex ideas more accessible.

Takeaways

• 😀 Vectors do not have a position; they are represented by arrows that indicate direction and magnitude.
• 😀 Coordinate systems are made up of an x-axis and y-axis, with the origin being the point where both axes intersect at (0, 0).
• 😀 The coordinates of a point on the coordinate system are determined by tracing lines parallel to the axes.
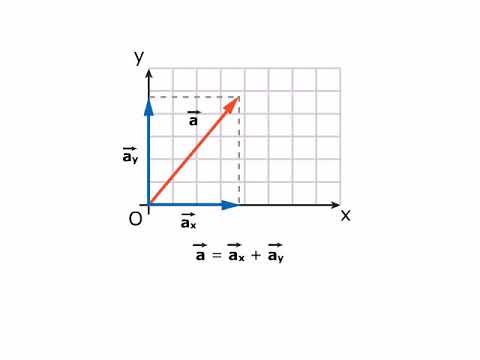
• 😀 A vector is defined by its components, which are the number of steps it takes horizontally (x-component) and vertically (y-component).
• 😀 Scalar multiplication scales a vector by multiplying each of its components by a scalar number, affecting its length.
• 😀 Scalar division is similar to multiplication, but the vector's components are divided by a scalar, shortening the vector.
• 😀 Vector addition is the process of summing the corresponding components of two vectors to create a resultant vector.
• 😀 Vector subtraction involves calculating the difference between two vectors by subtracting their respective components.
• 😀 The length (magnitude) of a vector can be calculated using the Pythagorean theorem, and it's represented as ||a||.
• 😀 A unit vector has a magnitude of 1 and can be created by dividing any vector by its own length.
• 😀 The dot product of two vectors measures how similar they are, and it is zero if the vectors are perpendicular.
• 😀 The cross product results in a vector that is perpendicular to the original vectors, and it is only defined in three dimensions.

Q & A

What is the purpose of a coordinate system in two dimensions?

A coordinate system in two dimensions is used to represent the position of points in a plane. It consists of two axes: the x-axis (horizontal) and the y-axis (vertical). By using these axes, we can assign coordinates to points based on their position relative to these axes.

How do you determine the coordinates of a point in a coordinate system?

To determine the coordinates of a point, you trace a line parallel to the y-axis to the x-axis and a line parallel to the x-axis to the y-axis. The intersection of these lines gives the x and y coordinates of the point.

What is the difference between points and vectors?

Points have a fixed position in space, whereas vectors do not have a fixed position. Vectors are represented by arrows and are defined by their length and direction, not their position.

What are vector components, and how are they calculated?

Vector components are the horizontal (x) and vertical (y) components of a vector. They are calculated by determining how many steps the vector moves in each direction: left or right for the x-component and up or down for the y-component.

Why is it important to write the x-component first and the y-component second when representing vectors?

It is important to write the x-component first and the y-component second to maintain consistency and clarity in vector notation. This order helps avoid confusion when dealing with multiple vectors.

What is the significance of the origin in a coordinate system?

The origin is the point where the x and y axes intersect. It has coordinates (0,0) and serves as the reference point for determining the position of all other points in the coordinate system.

What does scalar multiplication of a vector involve?

Scalar multiplication involves multiplying each component of a vector by a scalar (a number). This changes the vector's length but not its direction, unless the scalar is negative, which would reverse the direction of the vector.

What is vector addition, and how do you calculate it?

Vector addition involves combining two vectors by adding their corresponding components (x with x, y with y). The resulting vector starts at the tail of the first vector and ends at the tip of the second vector.

How can vector subtraction be visualized?

Vector subtraction can be visualized by reversing the direction of the vector being subtracted, then adding it to the first vector. This results in a vector that starts at the tip of the second vector and ends at the tip of the first vector.

What is the formula to calculate the length (magnitude) of a vector?

The length of a vector in two dimensions is calculated using the Pythagorean theorem: √(x² + y²), where x and y are the vector’s components. In three dimensions, the formula is extended to include the z-component.