[SER222] M02_02 The Sorting Lower Bound (4/4): The Result
Summary
TLDREn este video, se revisa el concepto fundamental de los algoritmos de ordenamiento, enfocándose en el límite inferior de O(n log n) para el tiempo de ejecución. Se discute cómo el algoritmo Mergesort es asintóticamente óptimo para los algoritmos basados en comparaciones, y cómo no es posible desarrollar ningún algoritmo de ordenamiento más rápido que este límite. A través de una prueba basada en árboles de decisiones, se demuestra que el tiempo de O(n log n) es una barrera permanente y universal, sin importar los avances tecnológicos en hardware o software. Mergesort se destaca como un ejemplo clave de un algoritmo eficiente dentro de este marco.
Please replace the link and try again.
Q & A
¿Cuál es el límite inferior para la complejidad temporal de los algoritmos de ordenación?
-El límite inferior para la complejidad temporal de los algoritmos de ordenación es n log n. Esto significa que ningún algoritmo de ordenación puede ser más rápido que n log n en el peor de los casos.
¿Por qué se considera que mergesort es un algoritmo asintóticamente óptimo?
-Mergesort es considerado asintóticamente óptimo porque es el algoritmo de ordenación más eficiente en términos de tiempo, con una complejidad de n log n, y no se puede mejorar su rendimiento en el contexto de algoritmos basados en comparaciones.
¿Qué implica que un algoritmo esté en el límite inferior de n log n?
-Significa que ningún algoritmo de ordenación, independientemente de las mejoras tecnológicas o de algoritmos que se desarrollen, podrá realizar la ordenación de forma más rápida que n log n en el peor caso para algoritmos que se basan en comparaciones.
¿Por qué no es necesario seguir buscando algoritmos de ordenación más rápidos?
-Porque ya tenemos varios algoritmos, como mergesort, que alcanzan el límite inferior de n log n, lo que implica que no se puede mejorar el rendimiento de la ordenación de manera significativa más allá de este punto.
¿Qué importancia tiene el hecho de que la prueba de límite inferior se base solo en la estructura del problema de ordenación?
-Es importante porque significa que el límite inferior de n log n no depende de lenguajes de programación específicos, arquitecturas de hardware ni implementaciones particulares. Es una conclusión universal que aplica a todos los contextos y tecnologías futuras.
¿Qué se entiende por 'prueba de límite inferior' en este contexto?
-Una prueba de límite inferior demuestra que no es posible mejorar el rendimiento de un algoritmo más allá de un cierto punto, en este caso, n log n para algoritmos de ordenación basados en comparaciones, independientemente de las circunstancias externas como la tecnología o el hardware.
¿Por qué se afirma que el resultado sobre el límite inferior es 'permanente'?
-Porque la prueba de límite inferior se basa únicamente en las características intrínsecas del problema de ordenación y no en condiciones específicas del sistema o el entorno, por lo que siempre será válida en el futuro, independientemente de los avances tecnológicos.
¿Qué implica que el resultado del límite inferior sea 'fuerte'?
-El resultado es considerado fuerte porque es una afirmación general y absoluta. No importa el algoritmo o el ordenador que se utilice, el límite inferior de n log n siempre se aplicará para la ordenación basada en comparaciones.
¿Cuál es la ventaja de conocer que no se puede superar el límite de n log n para ordenación?
-La ventaja es que los investigadores y desarrolladores pueden centrarse en mejorar otros aspectos de los algoritmos, como la eficiencia en el uso de memoria o la paralelización, sabiendo que no se puede mejorar el rendimiento en términos de tiempo más allá de n log n para ordenaciones generales basadas en comparaciones.
¿Por qué el algoritmo mergesort es considerado 'sencillo de explicar'?
-Mergesort es sencillo de explicar porque su enfoque se basa en dividir el problema en subproblemas más pequeños y ordenarlos recursivamente, lo cual es un concepto claro y fácil de entender, a pesar de ser un algoritmo con una complejidad temporal de n log n.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

[SER222] M02_02 Algorithm Analysis (3/3): What’s Next?

[SER222] Asymptotics (3/5): Lower Bounds

[SER222] M02_02 The Algorithm (1/8): Practical Sorting
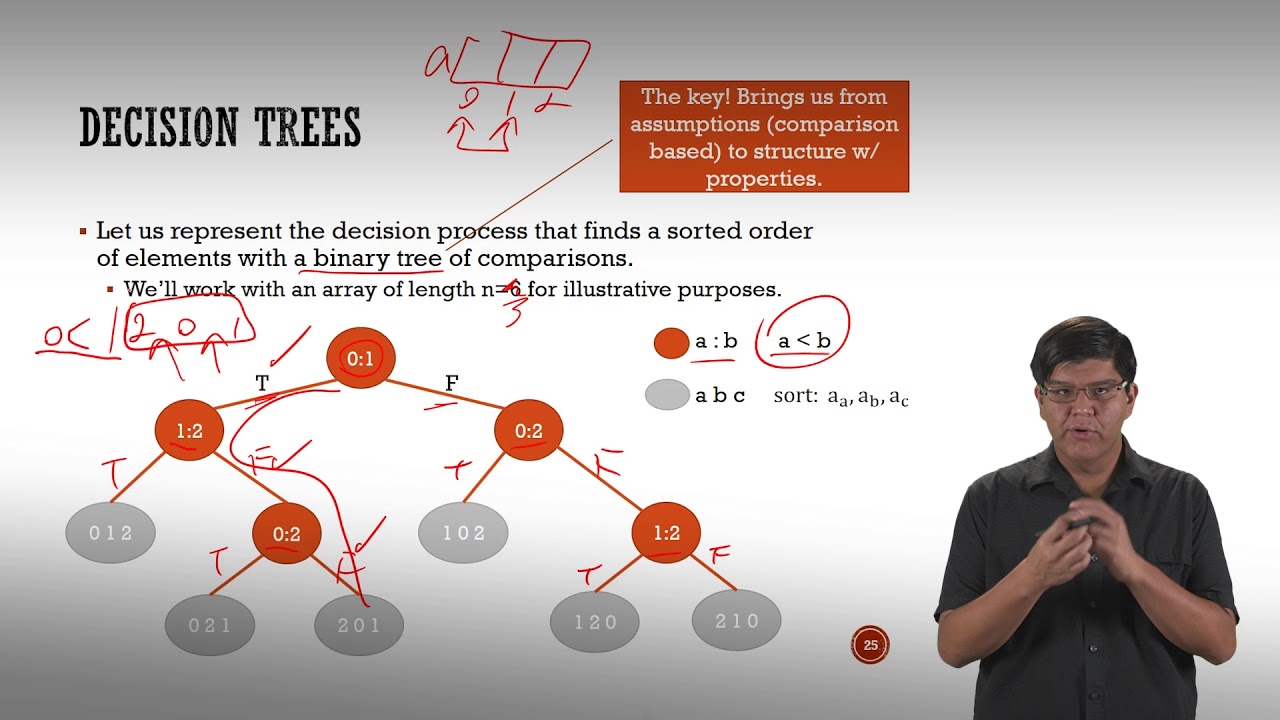
[SER222] M02_02 The Sorting Lower Bound (2/4): Decision Trees

[SER222] M02_02 The Algorithm (5/8): Visual Trace

[SER222] M02_02 The Algorithm (8/8): Performance [v2]
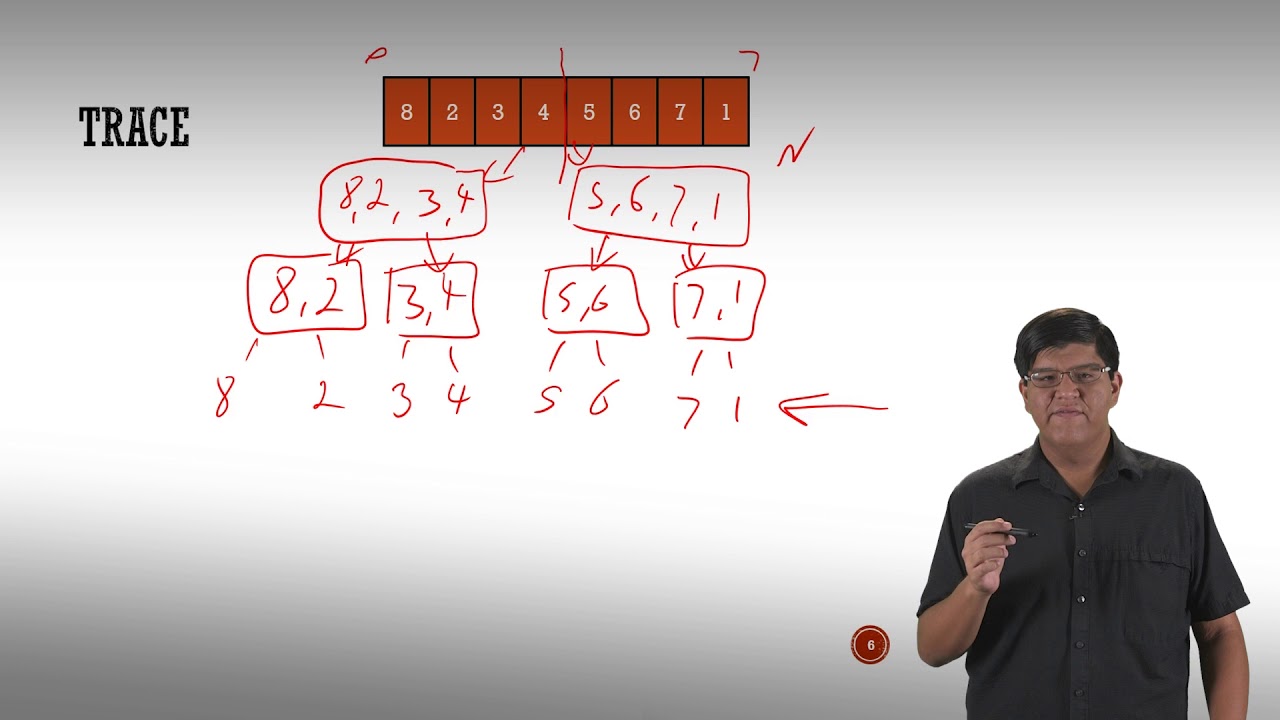
[SER222] M02_02 The Algorithm (4/8): Algorithm Trace
5.0 / 5 (0 votes)