🎡 Velocidad Angular (Movimiento Circular Uniforme) | MCU Video 7
Summary
TLDREn este video se explica cómo calcular el desplazamiento angular de la llanta de un automóvil dado su velocidad angular y el tiempo de rotación. Se presenta que la velocidad angular es de 75 radianes por segundo y que la llanta gira durante 30 segundos. Se utiliza la fórmula del movimiento circular uniforme para determinar que el desplazamiento angular es de 2,250 radianes. Luego, se convierte esta cantidad a vueltas, resultando en aproximadamente 358.5 vueltas. El video concluye invitando a los espectadores a suscribirse y compartir el contenido relacionado.
Takeaways
- 😀 La velocidad angular de la llanta de un automóvil es de 75 radianes por segundo.
- 🕒 El tiempo de rotación de la llanta es de 30 segundos.
- 🔄 Para calcular el desplazamiento angular, se utiliza la relación entre velocidad angular y tiempo.
- 📏 La fórmula para el desplazamiento angular es: desplazamiento angular = velocidad angular × tiempo.
- 🧮 Al sustituir los valores, el desplazamiento angular resulta ser 2,250 radianes.
- 🔄 Una vuelta completa equivale a 2π radianes (aproximadamente 6.2832 radianes).
- 🔄 Para convertir radianes a vueltas, se utiliza un factor de conversión de 2π radianes por vuelta.
- 📊 Al realizar la conversión, 2,250 radianes se convierten en aproximadamente 358.9 vueltas.
- ✅ Se redondea el resultado a un decimal: 358.9 vueltas.
- 👍 Conclusión: La llanta del automóvil dio 358.9 vueltas en 30 segundos.
Q & A
¿Qué información se proporciona al inicio del enunciado?
-Se proporciona la magnitud de la velocidad angular de la llanta, que es de 75 radiales por segundo, y el tiempo de giro, que es de 30 segundos.
¿Qué se necesita calcular a partir de la información dada?
-Se necesita calcular la magnitud del desplazamiento angular de la llanta en el tiempo especificado.
¿Cuál es la fórmula utilizada para calcular el desplazamiento angular?
-La fórmula utilizada es θ = ω × t, donde θ es el desplazamiento angular, ω es la velocidad angular, y t es el tiempo.
¿Qué valores se sustituyen en la fórmula para calcular el desplazamiento angular?
-Se sustituyen ω = 75 rad/s y t = 30 s en la fórmula, lo que resulta en θ = 2250 radianes.
¿Cómo se convierte el desplazamiento angular de radianes a vueltas?
-Se utiliza el factor de conversión de que 2π radianes es igual a 1 vuelta para realizar la conversión.
¿Cuál es el resultado de la conversión de 2250 radianes a vueltas?
-La conversión resulta en aproximadamente 358.5 vueltas.
¿Por qué es importante que las unidades de tiempo en la velocidad angular sean las mismas que las del tiempo?
-Es importante para asegurar la coherencia en las unidades y que los cálculos sean correctos.
¿Qué se concluye al final del cálculo sobre la llanta del automóvil?
-Se concluye que la llanta del automóvil dio 358.5 vueltas en un tiempo de 30 segundos.
¿Qué tipo de movimiento se menciona en la explicación del cálculo?
-Se menciona el movimiento circular uniforme.
¿Cómo se describe la presentación al final del video?
-Se invita a los espectadores a suscribirse y compartir el video, agradeciendo su visita.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

🎡 Velocidad Angular (Movimiento Circular Uniforme) | MCU Video 8

How to calculate angular speed of second, minute and hour hand
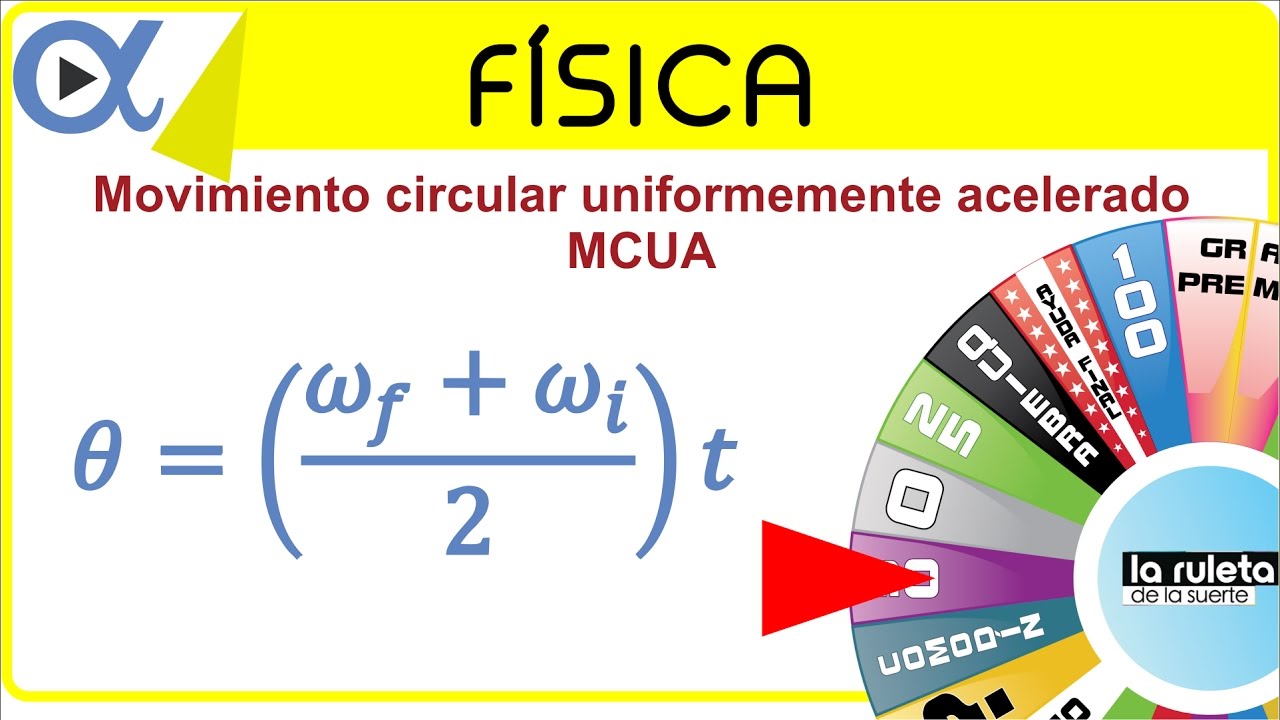
Movimiento circular uniformemente acelerado (MCUA) ejemplo 1 de 5 | Física - Vitual

Período y Frecuencia - MCU - Ejercicios Resueltos

✅MOVIMIENTO CIRCULAR EJERCICIOS | APRÉNDELO AHORA!!💯| FÍSICA PREPARATORIA

Movimiento Circular Uniforme MCU | Calcular rapidez angular y aceleración centrípeta
5.0 / 5 (0 votes)