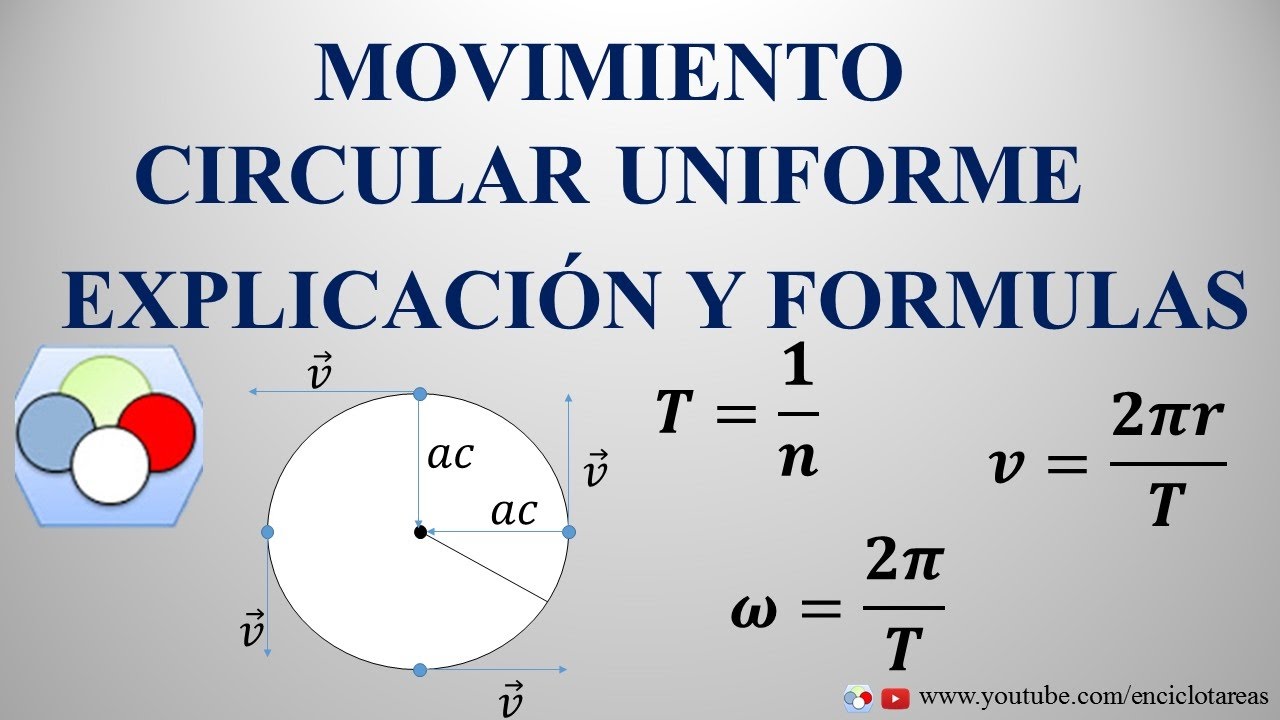
Movimiento Circular Uniforme MCU | Calcular rapidez angular y aceleración centrípeta

Summary

En este video, se abordan problemas de movimiento circular uniforme, enfocándose en el cálculo de la velocidad angular y la aceleración centrípeta. Se explica paso a paso cómo calcular la velocidad angular usando la fórmula basada en el número de revoluciones y el tiempo, y luego cómo hallar la aceleración centrípeta mediante la relación entre la velocidad angular y el radio. Se presentan ejemplos prácticos, incluyendo un ejercicio sobre la velocidad lineal y aceleración centrípeta de un disco, donde se realizan conversiones de unidades y se resuelven operaciones con precisión. Al final, se invita a los estudiantes a practicar más ejercicios.

Takeaways

• 😀 El movimiento circular uniforme (MCU) es un tema fundamental en la física, donde se estudian las relaciones entre las variables como la velocidad angular, la aceleración centrípeta y otros factores.
• 😀 Se explicó un problema donde se calcula la velocidad angular y la aceleración centrípeta de una partícula que gira a 2 metros de distancia, realizando 5 giros en 60 segundos.
• 😀 Para calcular la velocidad angular, se utiliza la fórmula ω = 2π * número de giros / tiempo, lo que da un valor de aproximadamente 0.5236 radianes por segundo.
• 😀 La aceleración centrípeta se calcula con la fórmula a_c = ω² * radio, utilizando la velocidad angular previamente calculada y el radio de 2 metros.
• 😀 En este ejemplo, la aceleración centrípeta resultó ser aproximadamente 0.5483 metros por segundo al cuadrado.
• 😀 La siguiente parte del video aborda un nuevo problema con un disco de 30 centímetros de diámetro que realiza 300 revoluciones por minuto, y se requiere calcular la velocidad lineal y la aceleración centrípeta.
• 😀 Se calcula el radio del disco, que es 15 centímetros, y se convierte a metros para poder usar las unidades del Sistema Internacional (SI).
• 😀 Para encontrar la velocidad lineal, se utiliza la fórmula v = 2π * número de giros * radio / tiempo, con los valores dados, resultando una velocidad lineal de aproximadamente 4.71 metros por segundo.
• 😀 Una vez obtenida la velocidad lineal, la aceleración centrípeta se calcula utilizando la fórmula a_c = v² / radio, dando un valor de aproximadamente 147.89 metros por segundo al cuadrado.
• 😀 El video enfatiza la importancia de usar una cantidad adecuada de decimales en los cálculos para obtener resultados precisos y cómo redondear según la necesidad.

Q & A

¿Qué es la velocidad angular en el movimiento circular uniforme?

La velocidad angular es la medida de la rapidez con la que un objeto rota alrededor de un punto central. Se calcula con la fórmula: ω = 2πn/T, donde n es el número de vueltas y T es el tiempo en segundos.

¿Cómo se calcula la aceleración centrípeta en el movimiento circular uniforme?

La aceleración centrípeta se calcula con la fórmula: a_c = ω² * r, donde ω es la velocidad angular y r es el radio de la trayectoria circular.

¿Cuál es la relación entre el radio y el diámetro en el contexto de este problema?

El radio es la mitad del diámetro. Si el diámetro es 30 cm, el radio será de 15 cm o 0.15 metros, que es la unidad adecuada para los cálculos.

En el primer ejercicio, ¿cómo se encuentra la velocidad angular?

Para encontrar la velocidad angular, se usa la fórmula ω = 2πn/T. En este caso, con 5 vueltas en 60 segundos, se calcula ω ≈ 0.5236 radianes por segundo.

¿Por qué la velocidad angular se expresa en radianes por segundo?

La velocidad angular se expresa en radianes por segundo porque los radianes son la unidad estándar en matemáticas y física para medir ángulos, y permiten calcular la velocidad de rotación de forma más precisa.

¿Qué datos son necesarios para calcular la aceleración centrípeta?

Para calcular la aceleración centrípeta, se necesita la velocidad angular y el radio de la trayectoria circular. La fórmula es a_c = ω² * r.

En el segundo problema, ¿cómo se convierte el diámetro a metros?

El diámetro es 30 cm, por lo que se divide entre 2 para obtener el radio de 15 cm. Luego, se convierte a metros dividiendo por 100, obteniendo 0.15 metros.

¿Cómo se calcula la velocidad lineal en el segundo ejercicio?

La velocidad lineal se calcula con la fórmula: v = 2πn * r / T, donde n es el número de revoluciones, r es el radio en metros, y T es el tiempo en segundos. En este caso, v ≈ 4.71 m/s.

¿Qué es la aceleración centrípeta y cómo se calcula en el segundo ejercicio?

La aceleración centrípeta es la aceleración que mantiene a un objeto en movimiento circular, siempre dirigida hacia el centro de la trayectoria. Se calcula con la fórmula: a_c = v² / r. Usando v ≈ 4.71 m/s y r = 0.15 m, se obtiene a_c ≈ 147.89 m/s².

¿Por qué se toma la aproximación en los cálculos de la velocidad angular y la aceleración centrípeta?

Se toma una aproximación porque en los cálculos se usan valores con decimales finitos, lo que implica que los resultados no son exactos, pero son suficientemente precisos para fines prácticos.