Cálculo del coeficiente de correlación r | Khan Academy en Español

Summary

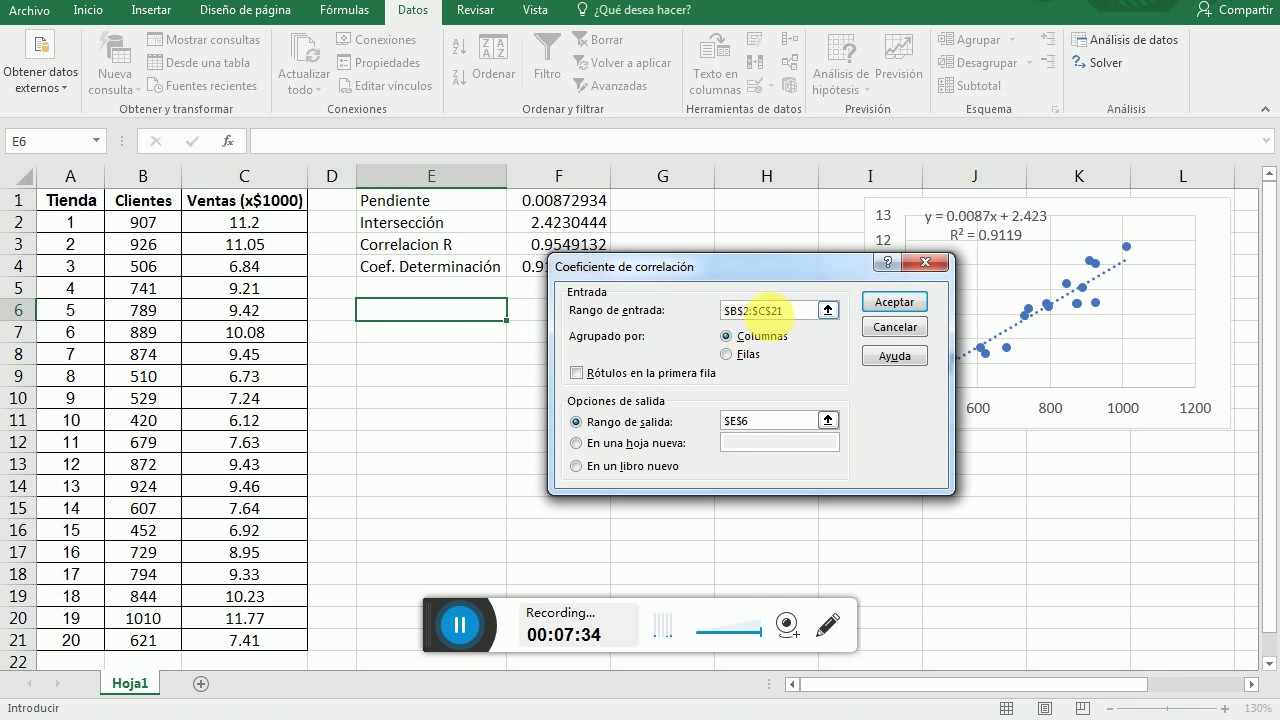
En este video, se explica el proceso de cálculo manual del coeficiente de correlación para un conjunto de datos bivariados. Se detallan los pasos para calcular la media y la desviación estándar de las variables X e Y, así como la importancia de los puntajes Z en la relación entre ambas. A través de un ejemplo práctico, se demuestra cómo se obtiene un coeficiente de correlación aproximado de 0.946, lo que indica una fuerte correlación positiva. El video también aborda la interpretación del coeficiente y la visualización de la relación mediante una gráfica, preparando el terreno para un análisis estadístico más avanzado.

Takeaways

• 😀 El coeficiente de correlación mide la relación entre dos variables bivariadas, es decir, cada valor de X tiene un correspondiente Y.
• 😀 La media muestral para una variable se calcula sumando todos los datos y dividiéndolos entre el número total de datos.
• 😀 La desviación estándar muestral se encuentra mediante la raíz cuadrada de la suma de las diferencias al cuadrado entre cada punto y la media, dividida por el número de datos menos uno.
• 😀 Los puntajes Z representan cuántas desviaciones estándar se aleja un valor de la media muestral.
• 😀 El coeficiente de correlación (r) se calcula como la suma de los productos de los puntajes Z de X y Y, dividido por n - 1.
• 😀 Un valor de r cercano a 1 indica una fuerte correlación positiva, mientras que un r cercano a -1 indica una fuerte correlación negativa.
• 😀 Si r es igual a 0, significa que no hay relación lineal entre las variables X e Y.
• 😀 En este ejemplo, el valor de r es aproximadamente 0.946, lo que sugiere una relación lineal fuerte entre las variables.
• 😀 Es importante entender cómo los puntajes Z influyen en el cálculo de r y cómo los datos que están en la media no contribuyen al coeficiente.
• 😀 Las herramientas informáticas son útiles para calcular coeficientes de correlación en conjuntos de datos más grandes, ya que el cálculo manual puede ser laborioso.

Q & A

¿Qué es el coeficiente de correlación y por qué es importante?

El coeficiente de correlación mide la relación entre dos variables, indicando si una variable tiende a aumentar o disminuir cuando la otra lo hace. Su valor varía entre -1 y 1, siendo crucial para entender la fuerza y dirección de la relación.

¿Cómo se calcula la media muestral para un conjunto de datos?

La media muestral se calcula sumando todos los valores de la variable y dividiendo entre el número total de observaciones. Por ejemplo, para los valores 1, 2, 2 y 3, la media es 2.

¿Cuál es la fórmula para calcular la desviación estándar muestral?

La desviación estándar muestral se calcula tomando la raíz cuadrada de la suma de los cuadrados de las diferencias entre cada valor y la media, dividida entre el número de datos menos uno.

¿Qué representan los puntajes Z en el contexto del coeficiente de correlación?

Los puntajes Z indican cuántas desviaciones estándar se aleja un valor de la media muestral. Se utilizan para calcular el coeficiente de correlación al comparar las distancias de los puntos a las medias muestrales.

¿Cómo se interpreta un coeficiente de correlación de 0.946?

Un coeficiente de correlación de 0.946 indica una fuerte correlación positiva entre las variables, sugiriendo que a medida que una variable aumenta, la otra también tiende a aumentar de manera consistente.

¿Qué implica un coeficiente de correlación de -1?

Un coeficiente de correlación de -1 indica una fuerte correlación negativa, lo que significa que cuando una variable aumenta, la otra disminuye en una relación lineal perfecta.

¿Por qué es relevante el número de datos al calcular el coeficiente de correlación?

El número de datos es relevante porque afecta el cálculo de la desviación estándar y, por ende, el resultado del coeficiente de correlación. Se utiliza n-1 para obtener una estimación más precisa de la población.

¿Qué sucede si el coeficiente de correlación es 0?

Un coeficiente de correlación de 0 sugiere que no hay relación lineal entre las variables, indicando que no se puede predecir el comportamiento de una variable a partir de la otra.

¿Cómo se realiza el cálculo del coeficiente de correlación paso a paso?

Se calculan primero los puntajes Z para cada par de datos, se multiplican los puntajes correspondientes y se suman los productos. Finalmente, se divide entre n-1 para obtener el coeficiente de correlación.

¿Cuál es la importancia de la representación gráfica al analizar la correlación?

La representación gráfica permite visualizar la relación entre las variables, ayudando a entender si la correlación es positiva, negativa o nula, y a identificar patrones o tendencias en los datos.