Estadística Datos Bivariados
Summary
TLDREn esta clase de estadística, se introducen los conceptos de datos bivariados, su representación mediante diagramas de dispersión y el análisis de correlación. Se explica la covarianza y su relación con la correlación lineal, destacando el uso del coeficiente de correlación de Pearson para determinar la fuerza y dirección de la relación entre dos variables. A través de ejemplos prácticos, como el análisis de resultados de exámenes, se demuestra cómo calcular y analizar la covarianza y el coeficiente de Pearson, concluyendo con una correlación positiva y fuerte entre las variables estudiadas.
Takeaways
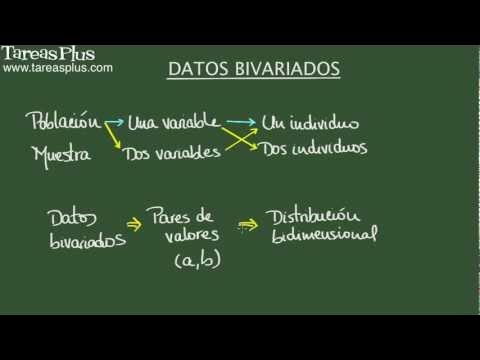
- 📊 En esta lección de estadística, se explica el concepto de datos variados, los cuales analizan dos variables sobre un mismo individuo o una variable sobre dos individuos.
- 🧮 Los datos variados se expresan mediante pares ordenados y se pueden representar en tablas o diagramas de dispersión para su análisis.
- 📉 En un diagrama de dispersión, los puntos que forman una línea recta inclinada a la derecha indican una correlación positiva y fuerte, mientras que si están dispersos, la correlación es débil.
- ⬇️ Si la nube de puntos está inclinada hacia la izquierda, esto indica una relación lineal negativa fuerte, pero si los puntos están más dispersos, la relación es débil.
- 📈 Cuando no hay una tendencia clara en los puntos, se considera que no existe una relación lineal entre las variables.
- 🔄 La covarianza es una medida que indica la relación lineal entre dos variables, y puede ser positiva (relación directa), cero (sin relación), o negativa (relación inversa).
- 📏 El coeficiente de correlación de Pearson establece una relación entre la covarianza y las desviaciones estándar de las variables, y varía entre -1 y 1.
- 📐 Si el coeficiente de correlación de Pearson es -1, hay una correlación negativa perfecta, si es 0, no hay correlación, y si es 1, es una correlación positiva perfecta.
- 📝 El ejercicio presentado analiza la relación entre los puntajes de simulacro y selección de 20 estudiantes mediante la covarianza y el coeficiente de correlación de Pearson.
- 🔍 El resultado final muestra un coeficiente de correlación de 0.93, lo que indica una correlación lineal positiva fuerte entre los puntajes, con un 93% de relación entre las variables.
Q & A
¿Qué se entiende por datos variados en estadística?
-Los datos variados se refieren a trabajar con dos variables sobre un único individuo o una variable sobre dos individuos simultáneamente. Esto implica el análisis de pares ordenados en una distribución bidimensional.
¿Cómo se representa gráficamente la relación entre dos variables?
-La relación entre dos variables se puede representar en un plano cartesiano mediante un diagrama de dispersión, donde cada par ordenado de datos corresponde a un punto en el plano.
¿Qué indica una relación lineal positiva y fuerte en un diagrama de dispersión?
-Una relación lineal positiva y fuerte se presenta cuando los puntos del diagrama de dispersión están inclinados hacia la derecha y se alinean casi en una línea recta, lo que indica una correlación positiva entre las variables.
¿Qué es la covarianza y qué nos indica su valor?
-La covarianza es una medida que indica la relación lineal entre dos variables. Si es mayor a 0, hay una relación lineal positiva; si es igual a 0, no hay relación lineal; y si es menor a 0, existe una relación lineal negativa.
¿Cuál es la fórmula para calcular la covarianza?
-La covarianza se calcula con la fórmula: Cov(xy) = sumatoria de (xi - x̄)(yi - ȳ) / n, donde x̄ y ȳ son las medias aritméticas de las variables x e y, respectivamente.
¿Qué representa el coeficiente de correlación de Pearson?
-El coeficiente de correlación de Pearson, representado por 'r', mide la fuerza y dirección de la relación lineal entre dos variables, con valores que oscilan entre -1 y 1.
¿Qué valores puede tomar el coeficiente de correlación de Pearson y qué significan?
-El coeficiente puede ser -1 (correlación negativa perfecta), 0 (sin correlación), o 1 (correlación positiva perfecta). Cuanto más cercano esté a -1 o 1, más fuerte es la correlación.
¿Cómo se calcula el coeficiente de correlación de Pearson?
-Se calcula como la covarianza dividida por el producto de las desviaciones estándar de las variables x e y. La fórmula es: r = Cov(xy) / (σx * σy).
¿Qué pasos se siguen para calcular la desviación estándar de una variable?
-La desviación estándar se calcula mediante la fórmula: σ = √[1/(n-1) * Σ(xi - x̄)²], donde 'n' es el número de datos, 'xi' son los valores individuales y 'x̄' es la media de esos valores.
¿Cuál fue la conclusión del ejercicio práctico sobre la correlación entre las pruebas de simulacro y selección?
-La conclusión fue que existe una correlación lineal positiva creciente y fuerte entre las pruebas de simulacro y selección, con un coeficiente de correlación de Pearson de 0.93, lo que indica un 93% de correlación.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)