Distancia entre dos puntos ejemplo 3 método gráfico
Summary
TLDREn este video, se explica cómo calcular la distancia entre dos puntos en un plano cartesiano utilizando el teorema de Pitágoras. Se toman como ejemplo los puntos A (-3,6) y B (1,3), que se ubican en el gráfico, y se dibuja un triángulo rectángulo. La distancia entre los puntos es la hipotenusa del triángulo, que se calcula sumando los cuadrados de los catetos y luego aplicando la raíz cuadrada. El resultado es que la distancia es 5 unidades. El instructor invita a los espectadores a seguir el curso completo y participar en la comunidad con comentarios y likes.
Takeaways
- 📏 El tema principal del video es cómo hallar la distancia entre dos puntos en un plano cartesiano.
- 📝 Se utiliza un gráfico para explicar el proceso, con los puntos A (-3, 6) y B (1, 3).
- 📊 Los puntos A y B son ubicados en el plano cartesiano en las coordenadas correspondientes.
- 📐 Para hallar la distancia, se dibuja un triángulo rectángulo donde la hipotenusa es la distancia entre los dos puntos.
- 🔺 Los catetos del triángulo tienen longitudes de 3 unidades y 4 unidades, respectivamente.
- 📚 Se aplica el teorema de Pitágoras para encontrar la hipotenusa, usando la fórmula: hipotenusa² = cateto₁² + cateto₂².
- 🔢 Los valores de los catetos son elevados al cuadrado (3² = 9 y 4² = 16), sumándose para obtener 25.
- ✔️ La hipotenusa es la raíz cuadrada de 25, lo que da un resultado de 5.
- ✏️ La distancia entre los puntos A y B es 5 unidades.
- 👋 Al final del video, se invita a los espectadores a ver el curso completo y a interactuar con el contenido (dar like, comentar, compartir).
Q & A
¿Qué puntos se utilizan en el ejemplo para calcular la distancia?
-Los puntos utilizados son A (-3, 6) y B (1, 3).
¿Cómo se determinan las coordenadas de los puntos en el plano cartesiano?
-Se ubican las coordenadas de acuerdo a los ejes x e y, donde A está en (-3, 6) y B en (1, 3), y se marcan en el plano.
¿Qué método se utiliza para calcular la distancia entre dos puntos?
-Se utiliza el teorema de Pitágoras, creando un triángulo rectángulo donde la hipotenusa es la distancia que se quiere calcular.
¿Cuáles son los catetos del triángulo rectángulo en este caso?
-Un cateto mide 3 unidades y el otro cateto mide 4 unidades.
¿Qué establece el teorema de Pitágoras?
-El teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Cómo se calcula la hipotenusa en este caso?
-Se suman los cuadrados de los catetos (3^2 = 9 y 4^2 = 16) para obtener 25, luego se saca la raíz cuadrada de 25, que es 5.
¿Qué representa la hipotenusa en este contexto?
-La hipotenusa representa la distancia entre los puntos A y B.
¿Por qué se aplica la raíz cuadrada al final del cálculo?
-Se aplica la raíz cuadrada para eliminar el exponente al cuadrado de la hipotenusa y obtener su valor real.
¿Qué letra se usa comúnmente para representar la distancia entre dos puntos?
-Generalmente se usa la letra 'd' para representar la distancia.
¿Qué pasos siguen después del cálculo para cerrar la explicación?
-El instructor invita a los estudiantes a ver el curso completo y a interactuar con el video (like, compartir, comentar).
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia Entre Dos Puntos En El Plano Cartesiano

Distancia entre dos puntos | Demostración de la fórmula

DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO
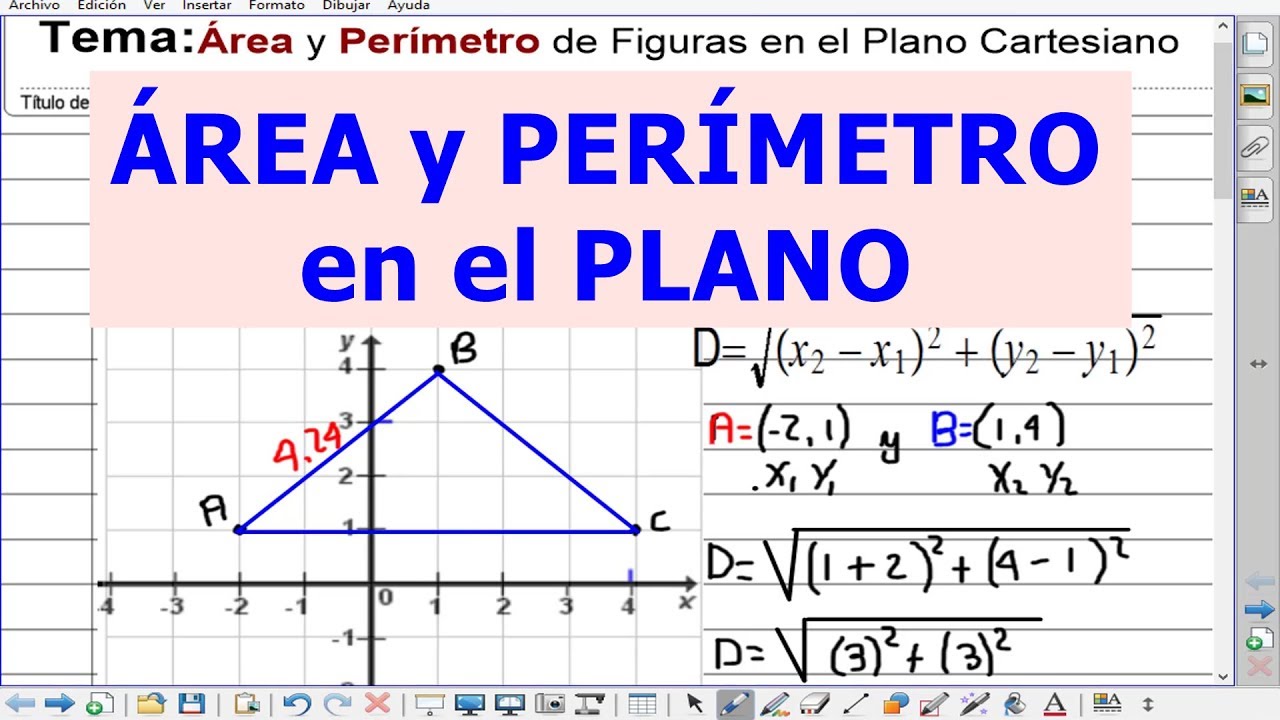
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)