Simpson 1/3 Introducción 01

MATHei

12 Dec 202012:52

Summary

TLDREl video explica el uso del método numérico de Simpson un tercio para aproximar el resultado de integrales definidas, a diferencia de métodos analíticos. A través de un ejemplo con la función seno de x al cuadrado, se muestra cómo interpolar un polinomio de segundo grado y luego calcular su integral para estimar el área bajo la curva. Aunque la calculadora utiliza una técnica diferente (cuadratura Gauss-Janě), el video destaca la importancia de entender diferentes enfoques numéricos para cálculos de integrales.

Takeaways

📊 El script讲解了如何在不具备解析解的情况下，使用数值方法来近似计算定积分。
🌟 特别提到了辛普森(Simpson)三分之一法则，尽管这不是计算器内部使用的计算方法。
📐 辛普森法则通过使用抛物线来近似函数曲线下的面积，从而计算积分。
🔢 首先，通过插值得到一个二次多项式，该多项式通过三个特定点（1.2, 1.4, 1.6）生成。
📈 通过计算器得到的数据点用于构建多项式，并计算其在给定区间的积分。
🏞️ 通过近似得到的积分结果与计算器直接给出的结果相近，但并不完全相同。
📝 计算器使用的是高斯-勒让德(Gauss-Legendre)求积法，这是一种特殊的高斯求积法。
🔍 虽然辛普森法则在视频中没有直接应用，但它提供了一种理解数值积分方法的途径。
🎯 辛普森法则的优势在于它简化了复杂函数的积分计算，使其变得更容易处理。
📊 视频中还提到了其他数值积分方法，如高斯求积法，这为理解更复杂的数值积分技术打开了大门。
🔑 了解数值积分方法的基本原理对于科学和工程领域的学生和专业人士来说非常重要。

Q & A

¿Qué método numérico se menciona en el script para aproximar el cálculo de integrales definidas?
-El método numérico mencionado en el script es el método de Simpson un tercio.
¿Qué es la técnica de fracciones parciales y por qué no se utiliza en este caso?
-La técnica de fracciones parciales es un método para resolver integrales definidas. No se utiliza en este caso porque el script se enfoca en explicar el aproximado numérico a través del método de Simpson un tercio en lugar de métodos analíticos como la técnica de fracciones parciales o sustitución trigonométricas.
¿Cuál es la función que se utiliza como ejemplo para explicar el método de Simpson un tercio?
-La función utilizada como ejemplo es f(x) = seno(x al cuadrado).
¿Qué representa la integral definida en relación a una curva y el eje x?
-Una integral definida representa el área que hay entre una curva y el eje x,限于 los límites inferior y superior especificados.
¿Cómo se aproxima el área en el ejemplo del seno de x al cuadrado utilizando el método de Simpson un tercio?
-Se aproxima encontrando una parábola que tenga un comportamiento similar al de la función en el rango de los límites y luego integrando esa parábola, lo que da un resultado aproximado al área bajo la curva original.
¿Qué es la parábola que se busca encontrar en el método de Simpson un tercio?
-La parábola buscada es una aproximación de la función original en un segmento específico de los límites, que se utiliza para calcular el área de manera numérica.
¿Cómo se obtiene el polinomio de segundo grado que se aproxima a la parábola en el método de Simpson un tercio?
-Se obtiene a través de la interpolación de un polinomio de segundo grado utilizando tres puntos en la curva, generalmente los límites y el punto medio entre ellos.
¿Cuál es el resultado aproximado del área en el ejemplo del seno de x al cuadrado?
-El resultado aproximado del área es de 0.34, aunque puede variar ligeramente dependiendo del método y la precisión del cálculo.
¿Qué es la cuadratura Gauss y cómo se relaciona con el método de Simpson un tercio?
-La cuadratura Gauss es un método numérico para aproximar integrales definidas. El método de Simpson un tercio es un caso especial de la cuadratura Gauss, y ambos son utilizados para aproximar el área bajo una curva a través de técnicas numéricas.
¿Qué método numérico se utiliza en la calculadora mencionada en el script?
-La calculadora mencionada en el script utiliza el método de Gauss-Legendre para la integración numérica.
¿Por qué es importante entender diferentes métodos numéricos para cálculos de integrales?
-Es importante entender diferentes métodos numéricos para cálculos de integrales porque cada uno tiene sus propias ventajas y limitaciones. Conocer varios métodos permite elegir el más adecuado para el problema específico, mejorar la precisión y la eficiencia del cálculo.

Outlines

00:00

📚 Introducción al Método Numérico de Simpson

En este primer párrafo, se presenta la tecla de la calculadora que permite realizar cálculos de integrales definidas. Se discute que, a diferencia de los métodos analíticos, el equipo utiliza un método numérico para aproximar resultados. Se menciona el Método de Simpson un Tercio como un ejemplo de cómo se aproxima el área entre una curva y el eje x, tomando como caso de estudio la función seno de x al cuadrado. Además, se sugiere que el objetivo es entender cómo la calculadora proporciona un resultado numérico sin realizar la integral de manera analítica.

05:02

📐 Estudio de la Aproximación con Polinomios

Este párrafo se enfoca en el proceso de aproximación de una función mediante polinomios. Se describe cómo, a través de la interpolación de un polinomio de segundo grado entre tres puntos, se puede obtener una parábola que se comporta de manera similar al trozo de función que se está analizando. Se detalla el proceso de calcular los valores y坐标 para completar la tabla de los puntos y se menciona cómo se utiliza la calculadora para obtener estos valores. Finalmente, se presenta el polinomio resultante y se discute cómo este polinomio permite calcular una integral que es más fácil de evaluar.

10:04

🔢 Ventajas del Método de Simpson un Tercio

En el tercer párrafo, se aborda la simplificación que ofrece el Método de Simpson un Tercio al transformar una integral complicada en una integral de un polinomio, lo que facilita el cálculo. Se menciona que, aunque no se requiere calcular el polinomio de interpolación para aplicar este método, se puede elegir cualquier punto para aproximar el resultado deseado. Además, se contrasta este método con otras técnicas numéricas más complejas como la Cuadratura Gauss y se señala que, aunque el Método de Simpson un Tercio no es el utilizado en todas las calculadoras, ofrece una base para entender métodos numéricos más avanzados.

Mindmap

Keywords

💡integrales definidas

Las integrales definidas son una extensión de las integrales, que permiten calcular el área bajo una curva y entre dos límites de integración. En el video, se utiliza este concepto para aproximar áreas utilizando métodos numéricos, como el método de Simpson un tercio, en lugar de resolver integrales de manera analítica. Un ejemplo se muestra al intentar calcular el área bajo la función seno de x al cuadrado entre los límites 1.2 y 1.6.

💡método numérico

El método numérico es un enfoque para aproximar soluciones a problemas matemáticos que no pueden ser resueltos exactamente o son demasiado complejos para una solución analítica. En el contexto del video, se utiliza el método numérico de Simpson un tercio para aproximar el área bajo una curva. Este método es útil cuando las técnicas de integración analíticas son infeasibles o complicadas.

💡Simpson un tercio

Simpson un tercio es un método numérico de integración que se utiliza para aproximar el valor de una integral definida. Consiste en interpolar una parábola a través de tres puntos y calcular la integral de esta parábola, lo que proporciona una aproximación del área bajo la curva original. En el video, se menciona este método como una técnica para aproximar el resultado de una integral definida, ilustrando su aplicación en el ejemplo de la función seno de x al cuadrado.

💡cuadratura de Gauss

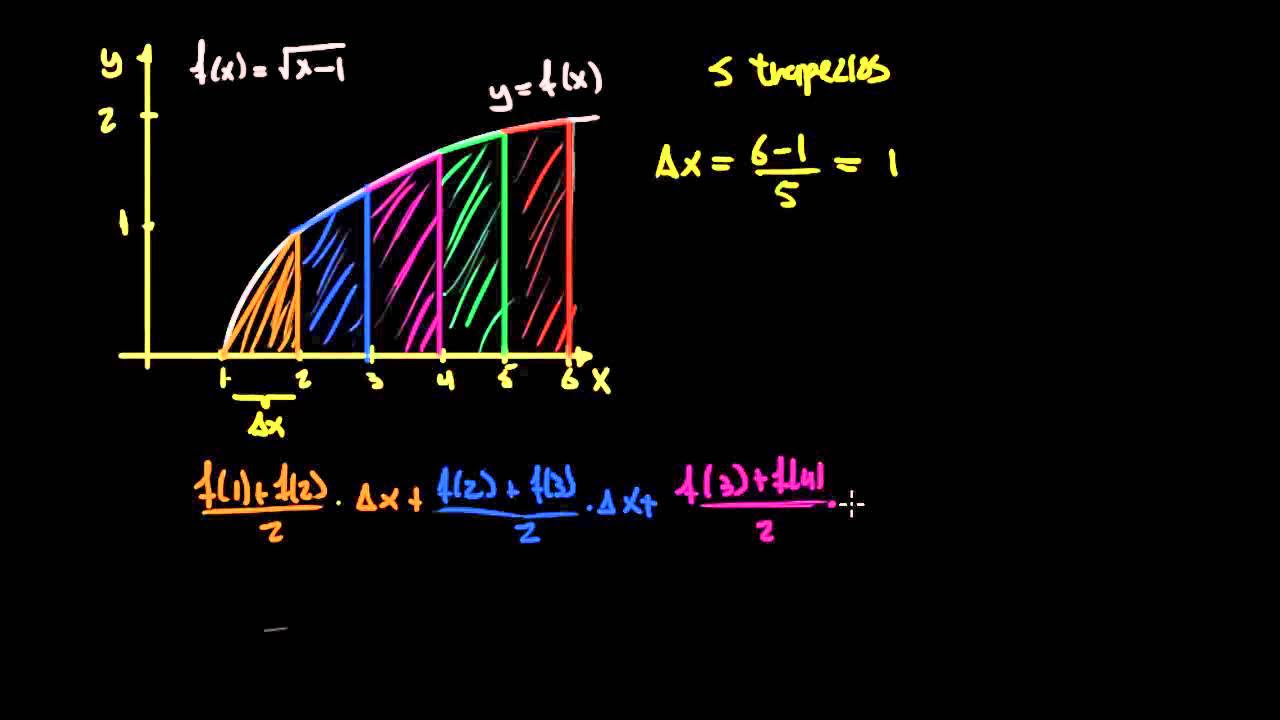
La cuadratura de Gauss es un método numérico avanzado para aproximar integrales definidas, que se basa en la distribución de puntos de evaluación y pesos para calcular el área bajo una curva. Este método es una generalización de otros métodos como Simpson un tercio y se caracteriza por su precisión en la aproximación. En el video, se menciona que la calculadora utiliza una técnica de cuadratura de Gauss, específicamente el método de Gauss-Radau, para resolver integrales numéricas.

💡polinomio de segundo grado

Un polinomio de segundo grado es una función matemática que se compone de términos que incluyen la variable al cuadrado, la variable y un término independiente. En el video, se utiliza para interpolar una parábola a través de tres puntos dados, lo que permite aproximar la función original y calcular la integral de la parábola, que es una aproximación del área bajo la curva original.

💡interpolación

La interpolación es el proceso de construir una función que pasa a través de un conjunto de puntos dados. En el video, se utiliza para encontrar un polinomio de segundo grado que se ajuste a tres puntos específicos y así aproximar la función original. Esta interpolación es clave para aplicar el método de Simpson un tercio y obtener una aproximación numérica de la integral.

💡área

El área en el contexto de integrales se refiere a la extensión de la región bajo la curva de una función y entre dos límites. En el video, el objetivo principal es calcular esta área utilizando métodos numéricos, ya que el resultado de una integral definida representa el valor de esta área.

💡límites de integración

Los límites de integración son los valores entre los cuales se calcula el área bajo la curva de una función en una integral definida. En el video, se establecen los límites 1.2 y 1.6 para calcular el área bajo la función seno de x al cuadrado.

💡aproximación numérica

La aproximación numérica es el proceso de estimar un valor desconocido a través de valores aproximados utilizando métodos matemáticos. En el video, se utiliza para estimar el área bajo la curva de una función a través del método de Simpson un tercio, que proporciona una aproximación del resultado exacto.

💡puntos de evaluación

Los puntos de evaluación son los valores específicos en los ejes x y y que se utilizan para construir una aproximación de una función o para calcular integrales numéricas. En el video, se eligen tres puntos para interpolar una parábola y aproximar la función original, permitiendo calcular la integral numérica.

💡función seno de x al cuadrado

La función seno de x al cuadrado es una función trigonométrica que representa el seno de un número elevado al cuadrado. En el video, se utiliza como ejemplo para ilustrar cómo se calcula la integral numérica utilizando el método de Simpson un tercio y cómo se aproxima el área bajo esta curva.

Highlights

El transcripto discute el uso de una calculadora para aproximar integrales definidas utilizando métodos numéricos.

Se menciona que la calculadora no resuelve la integral de manera analítica, sino que utiliza técnicas numéricas para aproximar el resultado.

El método numérico de Simpson un tercio es introducido como una técnica para aproximar áreas bajo una curva.

Se destaca la importancia de entender cómo funciona el equipo antes de obtener resultados numéricos.

Se utiliza la función seno de x al cuadrado como ejemplo para ilustrar el proceso de aproximación numérica.

Se describe el planteamiento de la integral definida y su relación con el área entre una curva y el eje x.

Se aborda el concepto de interpolación de un polinomio de segundo grado para aproximar la función dada.

Se menciona la obtención de tres puntos para la interpolación, utilizando los límites de integración y su valor medio.

Se calcula el polinomio de segundo grado que se aproxima a la función original en el rango de los límites.

Se verifica el resultado de la integral del polinomio aproximado utilizando una calculadora.

Se discute la diferencia entre el resultado exacto y la aproximación proporcionada por el polinomio.

Se menciona que el método de Simpson un tercio no requiere la interpolación de una parábola, sino que se puede aplicar directamente.

Se habla sobre la flexibilidad del método de Simpson un tercio para escoger diferentes coordenadas según la necesidad.

Se menciona que la calculadora utiliza una técnica de cuadratura Gauss-Legendre para la integración numérica, en lugar del método de Simpson un tercio.

Se sugiere que el método de Simpson un tercio es una herramienta útil para entender y aproximar integrales, aunque no sea el método utilizado en todas las calculadoras.

El transcripto invita a explorar métodos numéricos más complejos como la cuadratura Gauss-Legendre.