Gráfica de la función lineal | Ejemplo 1
Summary
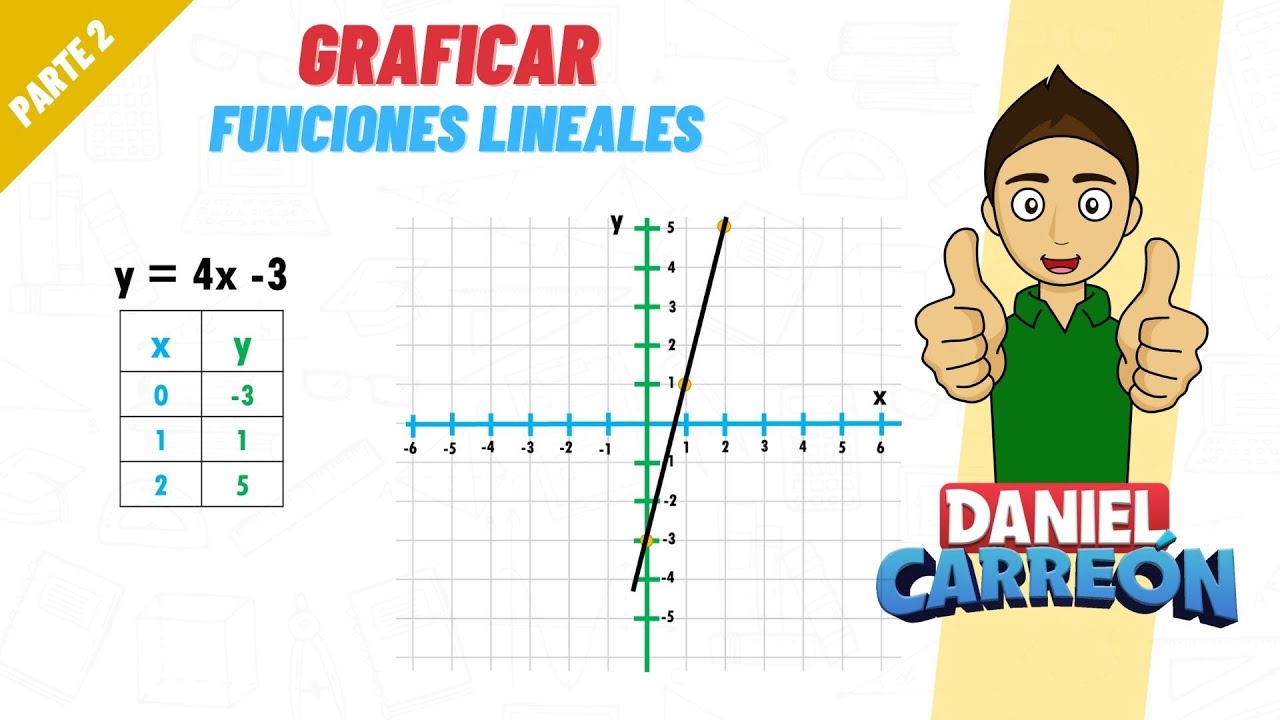
TLDREn este video, se enseña cómo graficar una función lineal, utilizando como ejemplo la ecuación y = 3x - 2. El instructor explica el uso de una tabla de valores para encontrar puntos clave en el plano cartesiano, sugiriendo trabajar con valores sencillos como 0, 1 y 2. Luego, muestra cómo realizar cálculos sencillos para obtener las coordenadas correspondientes y cómo trazar la gráfica, asegurándose de que los puntos formen una línea recta. El video también incluye recomendaciones para despejar la ecuación y evitar errores comunes al graficar.
Takeaways
- 📊 El video explica cómo graficar una función lineal usando una tabla de valores.
- ✏️ La función que se graficará es y = 3x - 2.
- 🗺️ Se utiliza un plano cartesiano y una tabla de valores para determinar puntos.
- ⚖️ Se recomienda usar tres valores para x, típicamente 0, 1, y 2, para facilitar el proceso.
- 📉 Se muestra que la función lineal solo tiene variables elevadas a la potencia de 1.
- 🔢 El proceso de sustitución implica reemplazar los valores de x en la función y hacer las operaciones correspondientes.
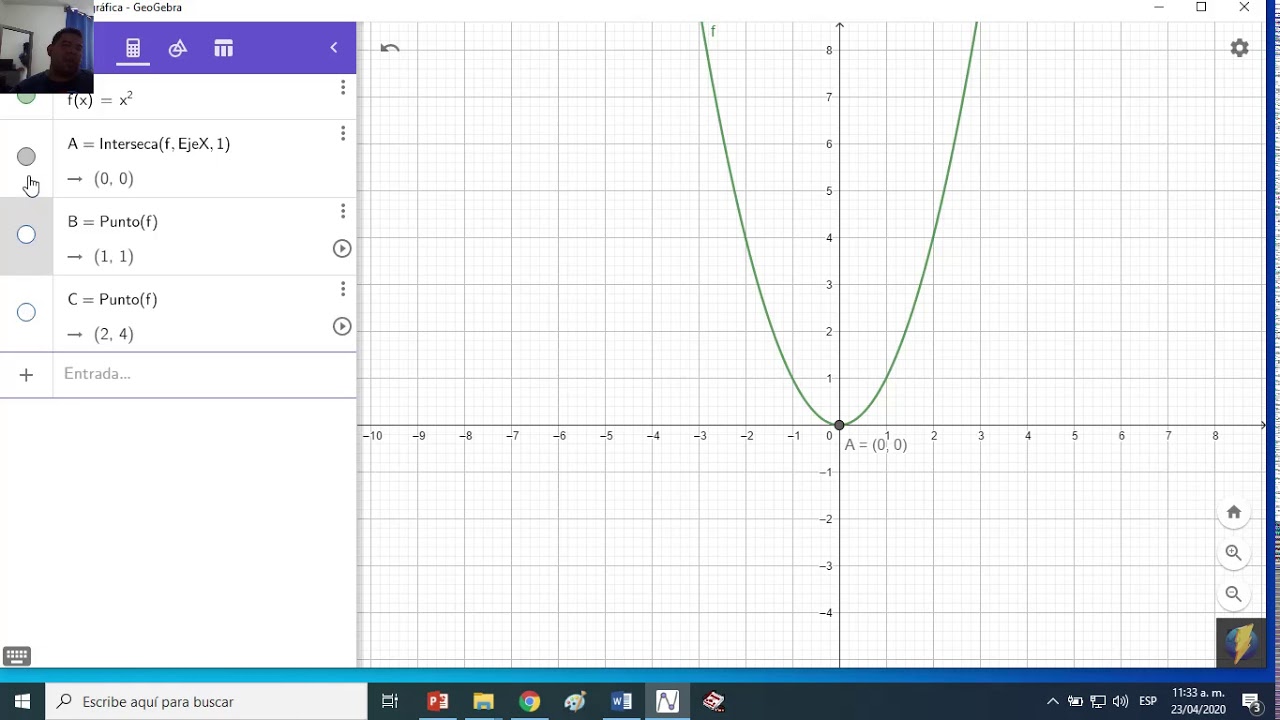
- 📍 Los puntos obtenidos se grafican en el plano cartesiano: (0, -2), (1, 1), (2, 4).
- 📐 Si los puntos forman una línea recta, la gráfica está bien hecha; si no, hay un error.
- 📏 Al unir los puntos en una línea recta, se extiende la línea hacia ambos lados.
- 📖 Se invita a los estudiantes a practicar con una nueva función y a revisar la respuesta al final del video.
Q & A
¿Qué función se está graficando en este video?
-Se está graficando la función lineal y = 3x - 2.
¿Qué método se utiliza para graficar la función?
-Se utiliza una tabla de valores donde se asignan valores a la variable x y se calculan los correspondientes valores de y.
¿Cuántos puntos recomienda el profesor para graficar la función y por qué?
-El profesor recomienda usar tres puntos, ya que con tres puntos es suficiente para graficar una línea recta en una función lineal.
¿Cuáles son los valores sencillos que el profesor suele elegir para la variable x?
-El profesor elige los valores 0, 1 y 2 para la variable x, ya que son más fáciles de calcular.
¿Qué recomienda el profesor si la función no está despejada para y?
-El profesor recomienda despejar la función para y antes de hacer los cálculos, lo que facilita encontrar los valores correspondientes de la variable.
¿Qué ocurre cuando una de las coordenadas de un punto es 0?
-Si una de las coordenadas es 0, el punto se ubica sobre el eje del número restante. Por ejemplo, si x = 0, el punto se ubica en el eje y.
¿Cómo se grafican los puntos obtenidos de la tabla de valores?
-Se colocan los puntos en el plano cartesiano según sus coordenadas y luego se unen con una línea recta para formar la gráfica de la función lineal.
¿Qué indica que la gráfica de la función es correcta?
-Si los tres puntos calculados caen en una línea recta, indica que la gráfica de la función es correcta.
¿Qué se debe hacer si los puntos no caen en línea recta?
-Si los puntos no caen en línea recta, es probable que haya habido un error en los cálculos y se deben revisar los valores asignados.
¿Dónde se puede acceder al curso completo de funciones mencionado en el video?
-El curso completo de funciones está disponible en el canal del profesor, en el enlace de la descripción del video o en la tarjeta que aparece en la parte superior del video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)