Gráfica de la función lineal | Ejemplo 2

Summary

En este video, el instructor enseña cómo graficar una función lineal despejando la variable y. A lo largo del proceso, ofrece consejos sobre cómo simplificar la ecuación y encontrar los puntos clave en una tabla de valores. Explica paso a paso cómo reemplazar valores en la ecuación y cómo graficar la función utilizando tres puntos. Además, da un ejercicio práctico para que los estudiantes lo resuelvan y refuercen lo aprendido. Al final, invita a los estudiantes a suscribirse y seguir el curso completo de funciones disponibles en su canal.

Takeaways

• 😀 Es importante despejar la 'y' en funciones lineales para facilitar la gráfica y el cálculo de los puntos.
• 😀 Para despejar la 'y', primero se deben mover los términos que no contienen 'y' al otro lado de la ecuación cambiando su signo.
• 😀 Después de despejar la 'y', se divide el término constante por el coeficiente numérico para encontrar la expresión final.
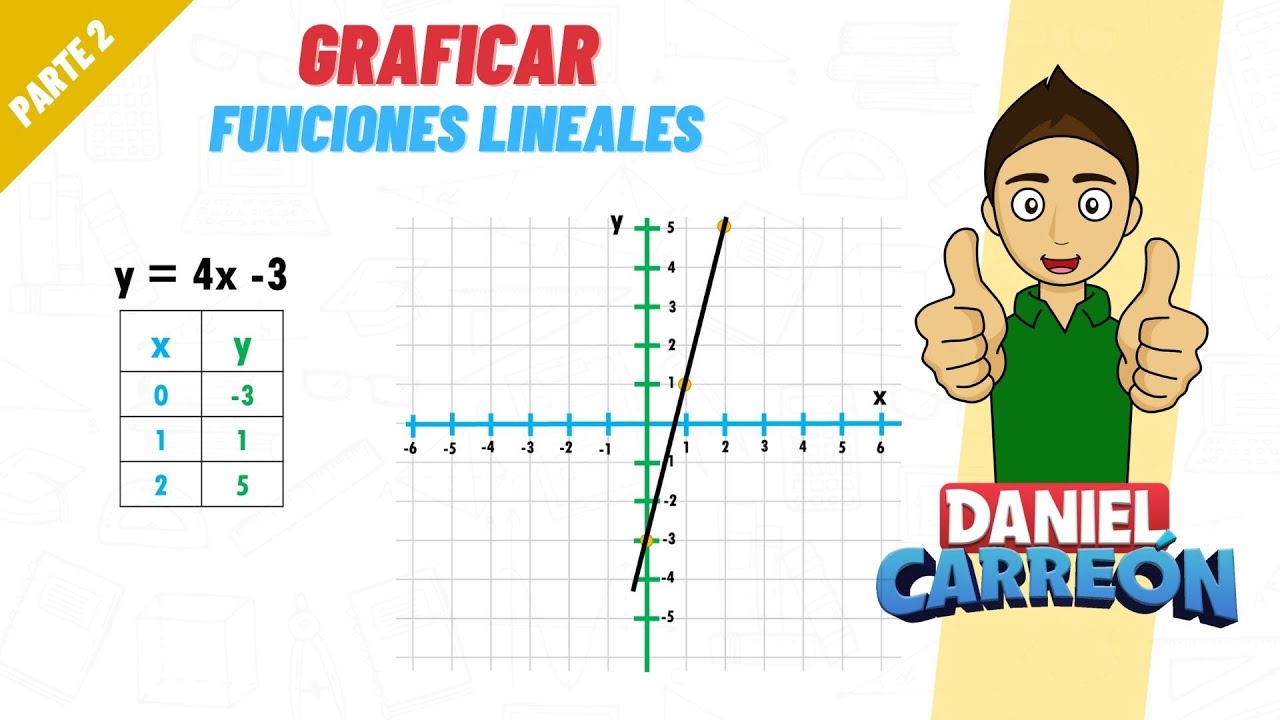
• 😀 Al graficar funciones, es útil utilizar una tabla de valores con al menos tres puntos. Los valores comunes para probar son 0, 1 y 2.
• 😀 La multiplicación siempre se realiza primero en los cálculos algebraicos antes de realizar cualquier suma o resta.
• 😀 La fracción resultante puede simplificarse si es posible; si no, se deja tal cual.
• 😀 Al graficar, se coloca cada punto correspondiente a los valores de la 'x' y 'y' en el plano cartesiano.
• 😀 En una función lineal, los puntos siempre deben alinearse en una línea recta, lo cual es clave para verificar si el gráfico es correcto.
• 😀 La recomendación es utilizar al menos tres puntos para asegurar la exactitud de la gráfica, aunque pueden añadirse más puntos si se desea.
• 😀 El proceso de despejar y graficar funciones puede parecer complicado al principio, pero con práctica, se vuelve más sencillo y rápido.

Q & A

¿Por qué es importante despejar la 'y' antes de graficar una función lineal?

Despejar la 'y' hace que sea más sencillo graficar la función, ya que permite expresar la ecuación en forma estándar, facilitando la identificación de los valores de la 'y' para distintos valores de 'x'.

¿Qué pasos se deben seguir para despejar la 'y' en una ecuación lineal?

Primero, se deben eliminar los términos que no contienen la 'y', moviéndolos al otro lado de la ecuación, lo que implica cambiar el signo de esos términos. Luego, se divide el término constante entre el coeficiente de la 'y'.

¿Por qué se recomienda usar valores simples como 0, 1 y 2 al crear la tabla de valores?

Se recomienda usar estos valores simples porque hacen los cálculos más fáciles y rápidos, permitiendo que los estudiantes visualicen más fácilmente cómo varía 'y' con respecto a 'x'.

¿Qué pasa si no se puede simplificar una fracción durante el cálculo de los puntos?

Si no se puede simplificar la fracción, se deja tal como está, ya que no es necesario simplificar todas las fracciones al graficar una función lineal.

¿Qué significa que la gráfica de una función lineal sea una línea recta?

Significa que todos los puntos que se grafican a partir de los valores calculados para 'x' y 'y' estarán alineados de forma continua y sin curvas, lo cual es característico de las funciones lineales.

¿Cuál es la recomendación sobre el uso de fracciones al graficar funciones lineales?

Aunque es posible usar fracciones, generalmente es más conveniente para los estudiantes trabajar con valores enteros, ya que facilitan el proceso de graficar y comprender los resultados.

¿Cómo se calcula el valor de 'y' cuando 'x' es igual a 0 en una función lineal?

Cuando 'x' es igual a 0, se sustituyen los valores en la ecuación para obtener 'y'. Por ejemplo, si la ecuación es 6 + 4x, al poner 'x = 0' obtenemos 'y = 3'.

¿Qué debo hacer si al realizar el despeje me encuentro con un término negativo?

Cuando te encuentras con un término negativo, este debe ser trasladado al otro lado de la ecuación cambiando su signo. Por ejemplo, un '-4x' se convertiría en '+4x' al trasladarlo.

¿Por qué se usa la multiplicación por -1 en algunos casos al despejar la 'y'?

Se multiplica por -1 para cambiar los signos de los términos de la ecuación, lo cual facilita el despeje de la 'y' cuando hay términos negativos involucrados.

¿Cuál es la diferencia entre un término positivo y un término negativo cuando se trasladan de un lado a otro de la ecuación?

Cuando un término positivo se traslada al otro lado de la ecuación, se convierte en negativo, y viceversa. Este cambio de signo es fundamental para el despeje correcto de la variable.