Statistics - Module 3 - Mean, Median, Mode, Percentiles and Quartiles - Problem 3-1B

Summary

This educational video script delves into statistical measures of central tendency, focusing on mean, median, and mode. It explains the arithmetic mean, or average, by demonstrating its calculation with a simple dataset. The script contrasts the mean's sensitivity to extreme values with the median's resilience, which divides a dataset into two equal halves. It also introduces the mode as the most frequent value, noting the possibility of multiple modes leading to a multimodal distribution. The presenter emphasizes the importance of understanding these basic concepts and their formal notation, as they form the foundation for more complex statistical analyses.

Takeaways

• 📊 The video discusses three measures of central tendency: mean, median, and mode.
• 🔢 The arithmetic mean (average) is calculated by summing all data points and dividing by the number of points.
• 📈 The mean is influenced by the magnitude of data points, unlike the median.
• 🎯 The median is the middle value in a data set, where 50% of observations are greater and 50% are lesser.
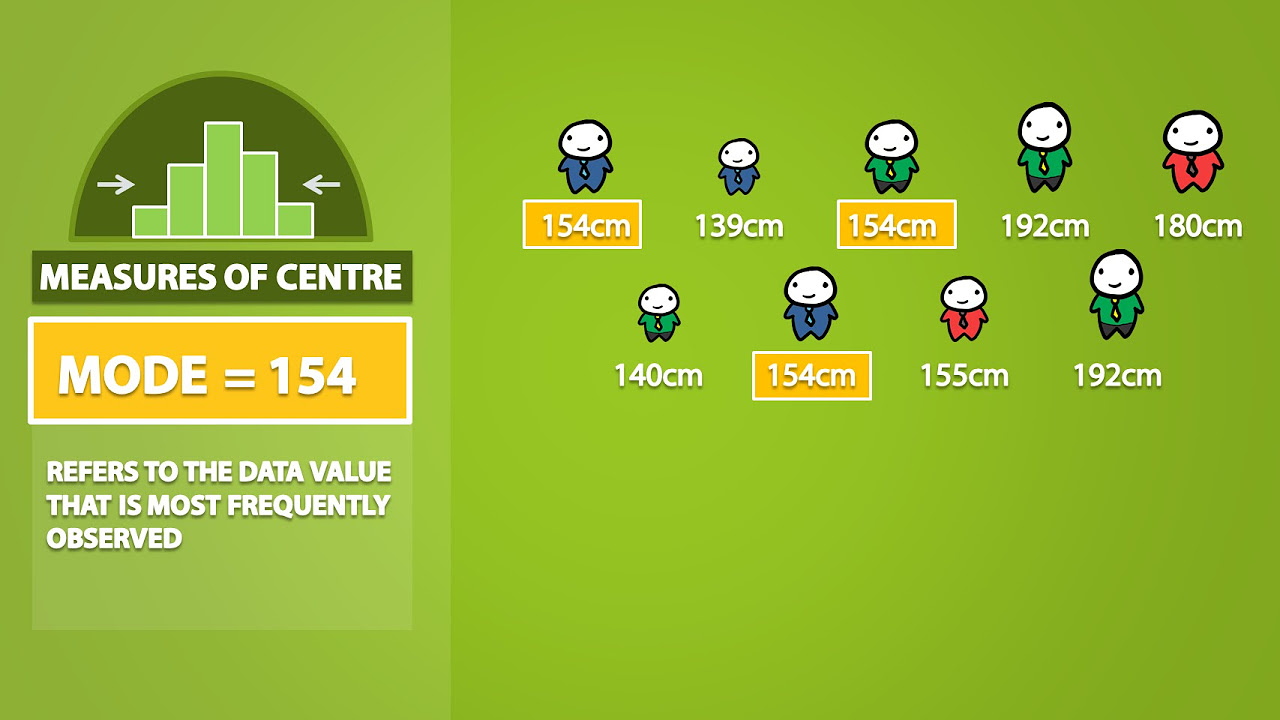
• 🔠 The mode is the value that occurs most frequently in a data set; a set can be unimodal, bimodal, or multimodal.
• ✅ The video demonstrates how to calculate mean, median, and mode using a sample of 30 company share prices.
• 📚 The script emphasizes the importance of understanding the notation and formulas for calculating mean, as they will be foundational for more complex concepts.
• 💡 The video provides a detailed walkthrough of calculating the mean, including the formula and its notation.
• 📋 The median is calculated by sorting the data and finding the middle value(s), which is crucial for even-numbered data sets.
• 🔍 The mode is identified by observing the frequency of each value in the sorted data set.
• 📝 The video concludes by reinforcing the importance of comfort with basic statistical calculations and notation for future learning.

Q & A

What are the three measures of central location discussed in the video?

The three measures of central location discussed in the video are mean, median, and mode.

What is the formula for calculating the arithmetic mean?

The formula for calculating the arithmetic mean is the sum of all data points divided by the number of data points.

How does the arithmetic mean differ from the median in terms of how it is influenced by the data points?

The arithmetic mean is influenced by the magnitude of the data points, while the median is not affected by the size of the values but rather their order.

What is the median and how is it found in a dataset?

The median is the value that separates the higher half from the lower half of a data sample. It is found by arranging the data points in order and picking the middle value or the average of the two middle values if there is an even number of observations.

What is the mode and how is it determined?

The mode is the value that occurs most frequently in a data set. It is determined by identifying the observation(s) that repeat the most.

Can a dataset have more than one mode? If so, what is it called?

Yes, a dataset can have more than one mode. If it has two modes, it is called bimodal, and if it has more than two, it is called multimodal.

What is the difference between the mean of a population and the mean of a sample?

The mean of a population is calculated using the entire dataset, while the mean of a sample is calculated using a subset of the population.

What is the notation used for the mean of a sample?

The notation used for the mean of a sample is x-bar (x̄).

How is the mean calculated when the number of observations is even?

When the number of observations is even, the mean is calculated by taking the average of the two middle values after the data has been sorted.

What is the importance of understanding the notation and formula for calculating the mean?

Understanding the notation and formula for calculating the mean is important because it provides a foundation for more complex statistical concepts and calculations that will be encountered in more advanced material.

Outlines

00:00

📊 Introduction to Measures of Central Tendency

The speaker begins by introducing the topic of the video, which is to explore various measures of location, specifically mean, median, and mode. The discussion starts with the mean, often referred to as the average. The arithmetic mean is explained as the sum of data points divided by the number of data points. An example is given using the data points 5, 5, 7, 10, and 14, which when summed and divided by 5, results in an arithmetic mean of 8.2. The speaker highlights that the mean is influenced by the magnitude of the data points, as changing one data point to 146 significantly alters the mean. This is contrasted with the median, which is the middle value when the data points are ordered, and is not affected by the magnitude of the data points. The mode, which is the value that occurs most frequently, is also introduced, and the concept of bimodal and multimodal data sets is briefly mentioned.

05:03

🔢 Formal Notation for Calculating the Mean

The speaker transitions to a more formal discussion of the arithmetic mean, emphasizing the importance of understanding the notation and formula used in calculations. Using the same data set from the previous example, the speaker assigns identifiers to each data point (x1, x2, x3, x4, x5) and explains that the mean is calculated by summing all observations (x1 through xn) and dividing by the number of observations (n). The generic formula for the mean is introduced, using the summation symbol to represent the sum of all xi values from 1 to n. The concept of a sample mean (x bar) is also explained, noting that it represents a subset of a larger population, using the Dow Jones Industrial Average as an example.

10:06

📈 Determining the Mode and Median of Share Prices

The speaker proceeds to an exercise involving the calculation of the mean, median, and mode of share prices for a list of 30 companies. The data is sorted from smallest to largest, which is beneficial for identifying both the median and mode. The mode is determined by identifying the observations that repeat, with the speaker noting that the highest frequency of repetition in the data set is twice, leading to multiple modes (30, 51, 100, and 132). To find the median, the speaker eliminates observations from both ends until reaching the middle of the data set, which in this case is a pair of observations (80 and 77). The median is then calculated as the average of these two values, resulting in 78.5.

15:06

💹 Calculating the Mean Share Price

Finally, the speaker calculates the mean share price for the 30 companies. The formula for the mean is reiterated, and the speaker demonstrates the calculation by summing all the share prices and dividing by the number of companies (30). The sum of the share prices is found to be 2558, and when divided by 30, the mean share price is calculated to be 85.26. The speaker concludes by emphasizing the importance of understanding the notation and formulas for calculating mean, median, and mode, as these concepts will become more complex in subsequent videos.

Keywords

💡Arithmetic Mean

The arithmetic mean, often referred to simply as the 'mean' or 'average,' is a measure of central tendency that represents the sum of a set of numbers divided by the count of numbers in the set. In the video, the arithmetic mean is calculated by adding together the data points (5, 5, 7, 10, 14) and then dividing by the number of data points (5), resulting in a mean of 8.2. This value is used to describe the central location of the data set, and it's sensitive to the magnitude of the data points, as changing the value of one data point (like increasing 14 to 146) significantly affects the mean.

💡Median

The median is another measure of central tendency that represents the middle value in a data set when the numbers are arranged in ascending order. If there is an even number of observations, as in the video's example with 30 companies, the median is calculated by averaging the two middle numbers after sorting the data. The video demonstrates this by sorting the share prices and then finding the average of the 15th and 16th values to get a median of 78.5. Unlike the mean, the median is not affected by the magnitude of the extreme values, making it a robust measure of central tendency.

💡Mode

The mode is the value that appears most frequently in a data set. In the context of the video, the mode is identified by looking for the data points that repeat, with the highest frequency being two occurrences for the values 30, 51, 100, and 132. The video explains that the data set is 'multimodal' because it has multiple modes. This is in contrast to a 'unimodal' distribution, which would have only one mode, and a 'bimodal' distribution, which would have two modes.

💡Central Tendency

Central tendency refers to a collection of measures that describe the center of a data set. In the video, central tendency is discussed in relation to the mean, median, and mode, which are all statistical measures used to represent the 'middle' or typical value of a data set. These measures help to summarize the data and provide a sense of its overall distribution.

💡Data Points

Data points are individual values within a data set. In the video, data points are the specific numbers that are used to calculate the mean, median, and mode. For example, the data points 5, 5, 7, 10, and 14 are used to calculate the arithmetic mean. Each data point contributes to the overall understanding of the data set's characteristics.

💡Observations

Observations are the individual items or measurements that are part of a data set. The video refers to observations when discussing the calculation of the mean, where each data point is considered an observation. The total number of observations (n) is crucial for calculating the mean, as it is the denominator in the formula for the arithmetic mean.

💡Sample Mean

The sample mean is the mean calculated from a subset of a larger population. In the video, the sample mean is denoted by the symbol 'x bar' and is calculated using the same formula as the arithmetic mean but is specifically used when the data set represents only a part of the whole population. The video emphasizes the importance of understanding the notation and formula for the sample mean, as it is foundational for more complex statistical concepts.

💡Notation

Notation in statistics refers to the symbols and shorthand used to represent mathematical operations and concepts. The video discusses the formal notation for calculating the mean, using the symbol Σ to represent the sum of all observations (xi) from i=1 to n. Understanding this notation is important for grasping more complex statistical formulas that will be introduced later in the course.

💡Dow Jones Industrial Average

The Dow Jones Industrial Average is a stock market index that represents the average of 30 significant stocks traded on the New York Stock Exchange and the NASDAQ. In the video, the Dow Jones Industrial Average is used as a context for the exercise of calculating the mean, median, and mode of share prices of 30 companies listed on the index.

💡Multimodal

A multimodal data set is one that has multiple modes, meaning there are several values that occur with the highest frequency. In the video, the data set of share prices is described as multimodal because there are four different values (30, 51, 100, and 132) that each appear twice, which is more frequent than any other values in the set.

Highlights

Introduction to measures of location: mean, median, and mode.

Definition and calculation of the arithmetic mean.

Explanation of how the mean is influenced by extreme values.

Introduction to the median as a measure of central tendency.

Demonstration of how the median is unaffected by the magnitude of data points.

Discussion on the mode as a measure of the most frequent observation.

Explanation of multimodal datasets and how to identify them.

Formal notation and formula for calculating the arithmetic mean.

Differentiation between calculating the population mean and sample mean.

Practical exercise on calculating the mean, median, and mode of share prices.

Sorting data to facilitate the identification of median and mode.

Identification of multiple modes in the dataset.

Manual calculation of the median for an even number of observations.

Calculation of the mean using the formula and practical data.

Final results of the mean, median, and modes for the sample of companies.

Emphasis on the importance of understanding basic statistical notation for future complex concepts.

Conclusion and summary of the video's educational content.

Transcripts

hello welcome back uh this in this video

we're going to look at various measures

of location specifically here we're

going to look at mean median and mode

now if

i begin with the discussion on mean

this is one that you've probably heard

of you've probably calculated it before

it usually goes by the name average

uh more specifically uh the type of mean

that we're going to look at here and the

one that you're probably most aware of

is called an arithmetic

mean

and

this is a mean that is had by adding

adding your data points together

and dividing by the number of of data

points that you have so for example if

you have

5

5 7 10

14

if those are your different data points

that you're working with

then in order to calculate the mean

i'm just getting myself a calculator

then you add these together 5 plus 5

plus 7 plus 10

plus 14.

so that equals 41.

so here i have my mean is 41 divided by

well how many observations do i have one

two three four five observations divide

that by five and here we get what is

called our arithmetic mean which is 8.2

so this value of 8.2

is one measure of what we call central

tendency or central location it's a

measure of roughly the middle in this

case 8.2 is somewhere around here

it's roughly the middle of that data set

now one of the characteristics about

this mean this arithmetic mean

is that it is influenced by the the

value of those numbers

if this wasn't a 14 if this was instead

146

well you can imagine this numerator is

going to be much larger

we still have five observations so this

ratio is going to end up being a lot

larger meaning our measure of mean is

going to be somewhere way out here

so having different values within your

data set influences where that mean

where that arithmetic mean

will will fall

this is opposed to

the median

the other measure of of central tendency

or central location

uh but really the median doesn't pay a

lot of attention to the the magnitude of

those observations if i start off here

with my original data set

so if i get rid of that 6 and here we

just have 14.

what is my median well the median is at

value

where 50 of your observations are

greater than or equal to the median and

50 percent of your observations are less

than or equal to the median

so in this exercise where i have five

observations here my median is this

point right in the middle it's a seven

fifty percent of my observations are

greater than or equal to and fifty

percent are down here so it's really

splitting it right in half

that doesn't change if this is a 14 or

if this is 146. my median is still in

exactly the same location

so unlike the mean the median is not

influenced by the relative magnitude of

those values of those data points

the mode

is similar in the sense that it's not

impacted by the magnitude of any given

observation but the mode is is uh

identified by finding the observation

that occurs with the highest frequency

so in this case i have

two fives a seven a ten let's go back to

our fourteen

so i have here the the fives occur twice

each of the other values only occur once

so this is then my mode

so it's possible to have one mode if i

had another 14 i could have two modes

and we would call this

bimodal

if i had

another ten i have two fives two tens

two fourteens then we would call it

multimodal and so we can have as many

modes

really any number of modes

it's a relatively little value at this

point to to get into the discussion of

multimodal

data sets that may come up a little bit

later when we talk about probability

in some of the later modules of this

course now

i want to

come back before we do this exercise

specifically i want to come back to this

discussion on the mean

partly because as much as you're aware

of how to calculate it

you've probably done it before i want to

just briefly talk about uh the formal

notation uh of the formula that is used

and that you've probably used without

even knowing it uh for calculating a a

mean an arithmetic mean

so what we're going to do i'll work with

the same

data set of these five observations

and i'm just going to replace or give

each one sort of an identifier so i'll

call each of these values x1 x2 x3

and x4 and x5

so these different x's these can really

take on any value okay so our five

in in the first case our first

observation now this five i can denote

it this is x1 this is my first

observation

x4 this is my fourth observation in this

case it happens to be 10

out here x5 is in this case 14 this is

my fifth observation

my data set consists of a total of five

observations so i would say

n equals in this example

five

okay now

notice that n equals five so i have five

observations my last observation that

subscript that five is the exactly the

same as the number of observations that

i have okay maybe that's obvious i don't

know

so when we're calculating the mean

uh regardless of how many observations

we have

we're adding together x1 plus x2 plus x3

in this case i'll work with just these

five observations we're adding together

all of our observations and we're

dividing it by n

the number of observations that we have

this is probably obvious you've probably

been doing this

any time you've calculated a mean

now when we write

the formula the more generic formula for

a mean

what we'll use the notation is this

symbol here which means

the sum

of

so the sum of so adding all of these

different observations together the sum

of x

i

where i is just an index i is a

placeholder

and it takes on every value from 1

through to n

so this is just a shorthand way

of writing

what i've got right here in the

numerator

so it's the sum of x equals one

here's one x equals two

i equals three sorry two and three and

four and five all the way

to n

representing however many

observations we have in that data set

and then finally

once we take the sum and we've added all

of these observations together then we

divide by n and that's just the same as

what we've done here

so for our means this is the formula

that we're using that we've always used

you've probably used it before without

really looking at it in this format and

if we're calculating what we call a

sample mean

then this is denoted by x bar so what i

mean by a sample mean is it's a subset

of the population so in this example

i have a share of 30 companies

on the dow jones this is only 30

companies this isn't all of the

companies it's not the full population

of companies this is just a sample of

30. it's a subset of 30. so here the

notation for a sample

is x bar

okay so that's maybe a little bit more

detail than you want um at this point of

how to calculate a mean but the reason

why i want to discuss it is because

this is the really the simplest formula

that we're going to

encounter in this in the sequence of

videos uh and i i really want whoever

whoever is watching to understand this

notation and understand these formulas

because as we progress through the more

difficult material

these types of formulas are going to

evolve and they're going to grow and are

going to become increasingly complex so

it's very helpful if at this stage in

the game you have a good understanding

and a good degree of comfort uh working

with

this

kind of notation because it's going to

be following us for a while

okay so enough about this let's get into

our exercise here so we've got this uh

list of 30 companies we want to

calculate the mean median and mode

share price now i think i've given

myself a cheat here so i've already

listed the companies i've relisted the

companies in one column

from smallest value

to the largest value

now sorting

your data like this

is helpful for

at least two things one

it's really imperative to have it sorted

like this in order to identify the

median value so that value that lies

right in the middle of the data set so

it's

imperative for identifying the median

for identifying the mode it's also

helpful because having it sorted from

smallest to largest any values that

repeat themselves which is necessary for

identifying a mode they'll all be

grouped together and so it's much easier

to see repeating observations because

they're all grouped together so

let's let's start off with the mode

because

really that's probably the easiest one

to spot we're just looking for

observations

that repeat so as i go through i'm just

going to look through and say well

there's two thirties

there's two fifty ones

uh there's two one hundreds

there's two 132s

and i don't see any observation that

repeats more than twice if if we had an

observation that repeated three or four

or five times

then these pairs that i've identified

here are no longer relevant um

but because the highest frequency of the

observation is two

uh then it becomes relevant and i have

it looks like three of uh four

observations one two

three four observations

each repeating twice

none that repeat more than twice

so these values 30

51

100 and 132

those are all my modes

so there's one mode

to

so this data set

is what we would call multimodal

uh it has multiple modes it has multiple

observations that

repeat uh the same frequency

uh

more than any others okay

so there's our mode uh let's find our

median so when we've got a nice a bigger

data set like this there's different

ways that we can go about finding a

median

in another video we'll show you a way

using a simple formula

in this exercise let's just do it sort

of the manual way where we'll go through

and eliminate observations starting with

the smallest and the largest

and so if we just go through our data

set

and eliminate

my pens not lining up

and eliminate individual observations

small and large

until we converge

to something in the middle

this would be a lot easier if my pen

lined up properly on the screen

and so here we are is that is that right

with a median this is not right because

i have an even number of observations so

i can't have fallen

directly on to one observation if i have

an even number

of observations

then

i must narrow down and be left with a

pair of observations what i did right

there i went through this exercise and i

came to one observation well that can't

be the case because i know i have 30

observations here

so i need to finish at a pair of

observations so let me try this again

and hopefully

i'll converge

to a pair

otherwise i know i've got a larger

mistake that i'll need to deal with

there

so now we've gone through and i've

gotten down to here this pair of

observations 80

and 77. i don't want to erase those in

the same sense that i've erased or

deleted the others because then i'm left

with nothing and that's not really

helpful

in identifying

my my

medium so what i want to do now is find

the middle

of those two remaining observations so

in this case it's uh this is going to be

80 plus 77 divided by 2

and so let me get my calculator

80 plus 77

divided by 2 so that gives me 78.5

and so that's my median

so half of my observations are less than

78.5

and half of my observations are greater

than 78.5

okay so we've got our modes four modes

multimodal we have our median

now let's calculate our mean and so our

mean here this is going to be x bar

equals and our formula again

this is

looking tedious let me actually change

my color

so x bar equals so the sum

observations

x i is i equals 1 through n and n in

this case is 30 because i know i have 30

observations

divided by n

which is 30.

so i'm going to erase all of my blue

lines here so i can see my observations

better

okay

now i need my calculator

and let's uh just go through with this

calculation it might take a few seconds

you're welcome to fast forward a little

bit i'm just going to punch in each of

these numbers add them together and

divide by 30. so let's get started 27

plus 30

30

54 57 62

63 64 65

71

almost there 129

132

132

148

155

168.

so 2558 is the numerator

divided by

30

equals 85.26

so this is 85.26

is my mean so this is my average share

price of these 30 uh different companies

taken off of the dow jones industrial

average

okay so there we have our mean our

median and our four modes in this case

for the sample of 30 shares from the dow

jones industrial average i hope that has

helped i'm going on to 18 minutes it's a

little bit longer than i wanted

but i really think it's important to

have spent some time going over the

details and then the notation and the

formula for something that is

understandably a simple complex a simple

concept simple calculation

but as i said before the more

comfortable you are with this notation

at this point

the better off you'll be as the material

progresses and evolves into more

difficult

concepts okay thank you very much for

watching