Mean, Median and Mode in Statistics | Statistics Tutorial | MarinStatsLectures
Summary
TLDRThis educational video script delves into measures of central tendency for numeric data, focusing on the mean, trimmed mean, median, and mode. It explains the sample mean, or arithmetic average, and its sensitivity to outliers. The concept of balance point is introduced to describe the mean visually. The median is discussed as a robust measure that divides data into halves, contrasting with the mean's tendency to be influenced by skewness. The trimmed mean, which removes extreme values, is briefly mentioned. Lastly, the mode as the most frequent value is introduced, noting its less common use in statistical analysis. The script emphasizes understanding these measures conceptually over manual calculation.
Takeaways
- 📐 The mean (also known as the arithmetic average) is a measure of central tendency that represents the average value of a numeric variable.
- 🎩 The mean is sensitive to outliers and can be pulled towards extreme values, making it less representative of the typical data point.
- 🔄 The concept of the mean can be visualized as a balance point, where the data set is evenly distributed around this point.
- ✂️ Trimmed mean is a variation of the mean that removes the top and bottom percentages of data to reduce the impact of outliers.
- 🔽 The median is the middle value of an ordered data set and is not affected by outliers, making it a robust measure of central tendency.
- 📊 The median divides the data set into two equal halves, with 50% of the data below and 50% above the median value.
- 📈 The mean and median can differ, especially in skewed distributions, where the mean may be pulled towards the direction of the skew.
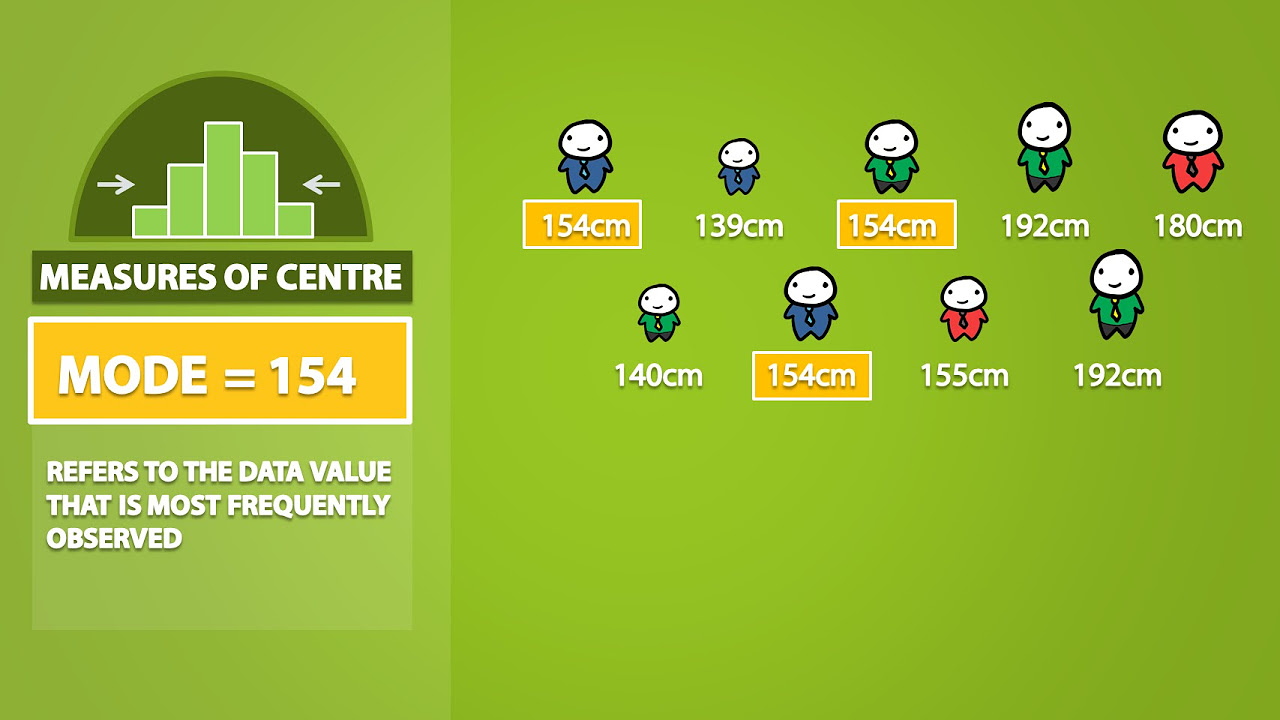
- 🏆 The mode is the most frequently occurring value in a data set and is a less commonly used measure of central tendency.
- 📚 Both parametric (like the mean) and nonparametric (like the median) measures are discussed, highlighting their different uses and interpretations.
- 💡 The script emphasizes understanding the concepts and interpretations of these measures over manual calculation, as software can easily compute them.
Q & A
What is the mean, also known as the arithmetic average?
-The mean, or arithmetic average, is a measure of central tendency that represents the average value of a numeric variable. It is calculated by summing all the values in a dataset and then dividing by the total number of observations.
What is a trimmed mean and how is it different from the regular mean?
-A trimmed mean is a type of mean calculated after removing a certain percentage of the highest and lowest values from the dataset. This is done to make the mean less sensitive to outliers. It differs from the regular mean in that it doesn't consider the full range of data points.
How is the median defined and how does it differ from the mean?
-The median is the middle value of an ordered dataset, dividing it into two equal halves. It differs from the mean in that it is not affected by outliers or extreme values, making it a more robust measure of central tendency for skewed distributions.
What is the mode and why is it less commonly used in statistical analysis?
-The mode is the most frequently occurring value in a dataset. It is less commonly used in statistical analysis because it doesn't provide as much information about the central tendency of the data as the mean or median, especially for datasets that do not have a clear single mode.
How does the mean represent a balance point for the data?
-The mean is considered a balance point because it is the point at which the sum of the deviations of each observation from the mean is minimized, conceptually balancing the data around a central value.
What is the difference between a parametric and nonparametric measure?
-Parametric measures, like the mean, make assumptions about the distribution of the data (e.g., normality) and use parameters to describe the data. Nonparametric measures, like the median, do not rely on these assumptions and are often used with non-normally distributed data or when the data does not meet the assumptions required for parametric tests.
How sensitive is the mean to outliers, and why?
-The mean is highly sensitive to outliers because it is influenced by the magnitude of all the values in the dataset. Outliers, being extreme values, can significantly pull the mean towards them, affecting the central tendency representation.
Why might the median be a more useful measure than the mean for certain types of data?
-The median might be more useful than the mean for data with outliers or skewed distributions because it is not affected by extreme values. This makes it a more reliable measure of central tendency for such data, providing a better representation of the 'typical' value.
How is the concept of 'balance point' used to understand the mean?
-The concept of 'balance point' is used to understand the mean by imagining the data points as weights on a balance scale. The mean is the point at which the scale would be perfectly balanced, with no tilt towards any side, representing the average position of all data points.
What is the significance of the notation used in statistical formulas, and why is it important?
-The notation used in statistical formulas is significant because it provides a concise and standardized way to represent complex mathematical concepts. It allows for clear communication among statisticians and helps in understanding the underlying principles without getting lost in the details of verbal explanations.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Ch 3 Lecture Video, Fall 2024: Measures of Central Tendency

Ukuran Pemusatan Data Kelompok

UKURAN PEMUSATAN DATA BERKELOMPOK | Rataan Median Modus Kuartil Desil Persentil

STATISTIKA: Ukuran gejala pusat dan ukuran letak 1
Mode, Median, Mean, Range, and Standard Deviation (1.3)

Statistika Dasar Ukuran Pemusatan Data (Mean, Modus, Median) Data Tunggal dan Data Kelompok
5.0 / 5 (0 votes)