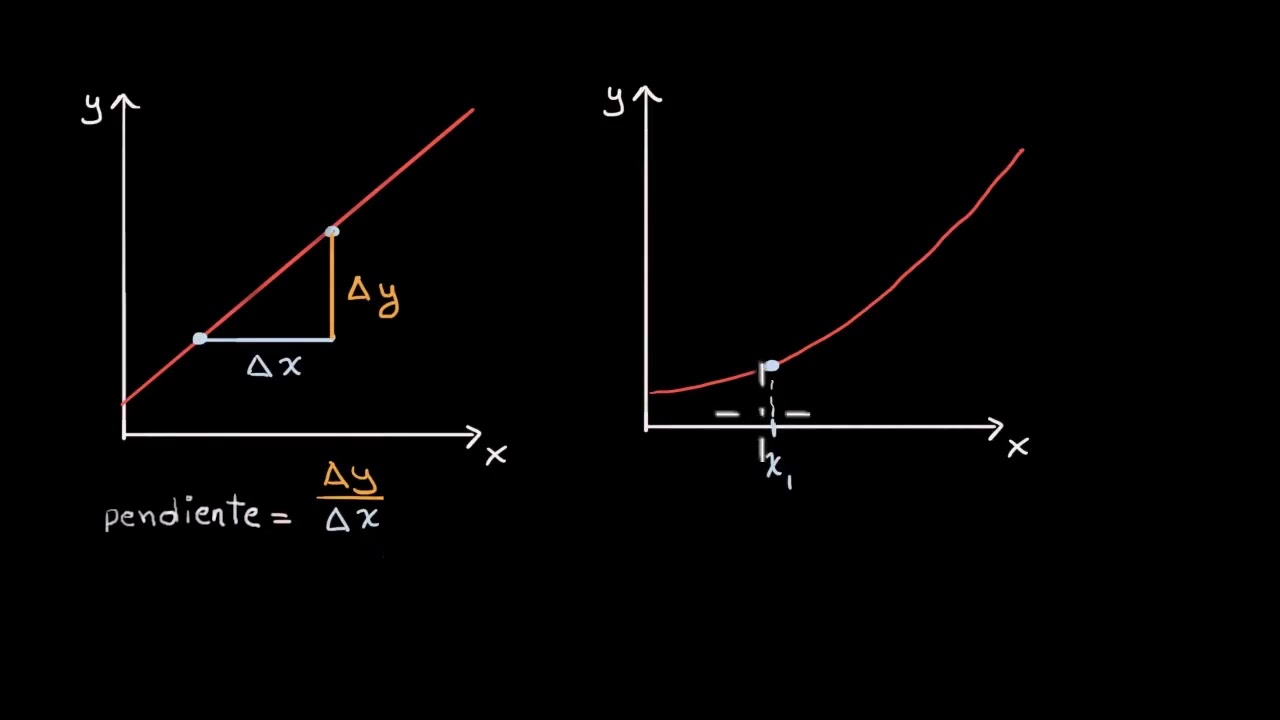El concepto de derivada. ¿Qué es y para qué sirve la derivada?
Summary
TLDREl guión explora la definición de la derivada en cálculo diferencial, desmitificando su concepto como una 'tasa de cambio instantánea'. A través de un ejemplo de competencia de robótica, se ilustra cómo calcular la velocidad en cada instante para asegurar que no se supere un límite de velocidad. Se explica que la derivada es la mejor aproximación a la pendiente de la recta tangente en un punto, y cómo esta técnica permite obtener una gráfica de velocidad que describe el cambio de velocidad a lo largo del tiempo, sin necesidad de conocer la función original.
Takeaways
- 😀 La derivada se describe como una 'tasa de cambio instantánea' para cada punto de una función.
- 🤔 Se cuestiona cómo es posible medir una tasa de cambio en un solo instante, lo que parece contradictorio.
- 🤓 La derivada es a menudo enseñada como una operación mágica sin una comprensión profunda de su significado.
- 🤖 Se utiliza el ejemplo de una competencia de robótica para ilustrar la necesidad de entender la derivada para evaluar si un robot ha superado un límite de velocidad.
- 📈 Se discute cómo la velocidad promedio calculada a lo largo de un intervalo de tiempo no puede representar la velocidad instantánea.
- 🔍 Se explora la idea de que la derivada es una aproximación a la recta tangente en un punto específico de una función.
- 📉 Se muestra que al dividir el tiempo en intervalos más pequeños, las velocidades promedio calculadas se acercan más a la velocidad real del robot.
- 📘 Se explica que la derivada es una forma de medir el cambio en el eje vertical de una función (cambio en y) por el cambio en el eje horizontal (cambio en x).
- 📊 Se utiliza el concepto de límites para definir formalmente la derivada, donde se considera lo que sucede cuando el cambio en el eje horizontal se hace muy pequeño.
- 🏁 Se concluye que la derivada es una herramienta poderosa para entender cómo cambia una función a lo largo del tiempo, permitiendo evaluar reglas como límites de velocidad sin conocer la función completa.
Q & A
¿Qué es una derivada y cómo se relaciona con la tasa de cambio instantáneo?
-Una derivada es una operación matemática que, dada una función, devuelve otra función que representa la mejor aproximación a la recta tangente en un punto específico. Se relaciona con la tasa de cambio instantáneo porque muestra cómo cambia una cantidad respecto a otra en un instante específico, en lugar de un promedio sobre un intervalo de tiempo.
¿Por qué es difícil entender la noción de tasa de cambio instantáneo en una función?
-Es difícil porque la tasa de cambio tradicionalmente implica un cambio entre dos momentos, mientras que la derivada busca describir el cambio en un único instante, lo cual parece contradictorio al principio.
¿Cuál es la diferencia entre la velocidad promedio y la velocidad instantánea?
-La velocidad promedio es el cambio en la posición de un objeto dividido por el tiempo transcurrido entre dos puntos en el tiempo, mientras que la velocidad instantánea es la velocidad en un solo punto en el tiempo, que se obtiene tomando el límite cuando el intervalo de tiempo tiende a cero.
¿Cómo se utiliza el concepto de derivada en la competencia de robótica mencionada en el guion?
-En la competencia de robótica, el concepto de derivada se utiliza para determinar si el robot ha sobrepasado el límite de velocidad en algún momento de su recorrido, analizando la gráfica de posición contra tiempo y calculando la pendiente (velocidad instantánea) en diferentes puntos.
¿Qué es la pendiente en el contexto de la derivada y cómo se relaciona con la velocidad?
-La pendiente en el contexto de la derivada es el coeficiente que multiplica al cambio en el eje horizontal (tiempo) para obtener el cambio en el eje vertical (posición), y se relaciona con la velocidad porque representa la tasa de cambio de la posición con respecto al tiempo.
¿Qué significan los símbolos 'delta' (Δ) y 'd' en el contexto de las derivadas?
-El símbolo 'delta' (Δ) representa la diferencia entre dos valores, mientras que 'd' se utiliza cuando se considera un cambio infinitesimalmente pequeño, aproximándose a cero, y es una forma de notar diferencias cuando se analiza la derivada.
¿Cómo se define formalmente una derivada en términos de límites?
-Una derivada se define formalmente como el límite cuando el intervalo de tiempo tiende a cero de la razón entre el cambio en el eje vertical (Δy) y el cambio en el eje horizontal (Δx), es decir, la pendiente de la recta tangente en el punto de interés.
¿Qué es la recta tangente y cómo se relaciona con la derivada?
-La recta tangente es la línea que toca la curva de una función en un punto sin cruzarla, y se relaciona con la derivada porque la pendiente de esta recta es igual a la derivada de la función en ese punto, representando la mejor aproximación a la tasa de cambio instantánea.
¿Cómo se puede visualizar el proceso de aproximación a la derivada a través de la división en intervalos más pequeños?
-A medida que se divide la gráfica de posición en intervalos más pequeños, las velocidades promedio calculadas para cada intervalo se aproximan más a la velocidad instantánea real, lo que se visualiza en la gráfica de velocidad creando una aproximación cada vez más precisa a la función de velocidad.
¿Qué conclusiones se pueden sacar sobre la velocidad de los robots en la competencia basadas en las gráficas de velocidad obtenidas?
-Las gráficas de velocidad obtenidas a partir de las derivadas nos permiten determinar si un robot ha violado el límite de velocidad en algún momento de su recorrido, pudiendo así descalificarlo si es necesario.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)