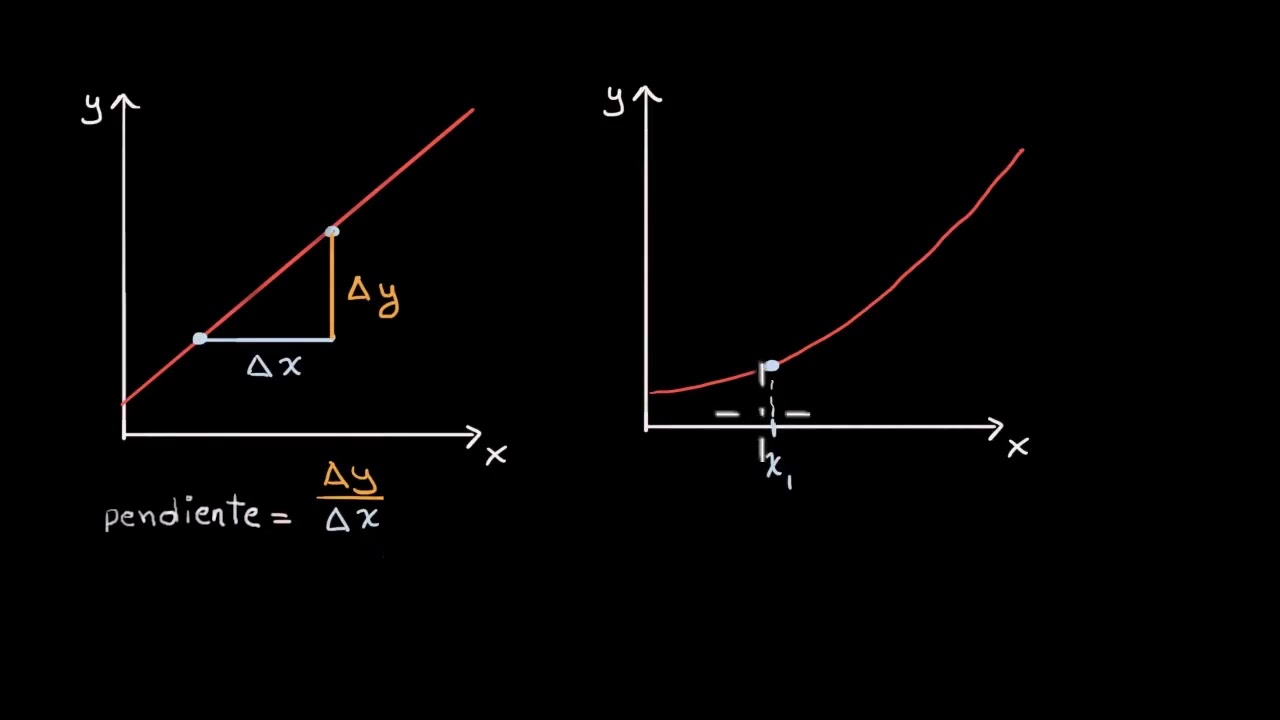HISTORIA DEL CALCULO DIFERENCIA

Summary

Este guion explora el concepto del cálculo diferencial y su importancia en diversas disciplinas como la física y la música. A través de una narración histórica que abarca desde la antigua Grecia hasta Galileo Galilei, se explica cómo las matemáticas y la armonía se interrelacionan. Se profundiza en el concepto de derivada, su aplicación en la cinemática y otras áreas como la velocidad instantánea y la pendiente de una curva. A lo largo del guion, se presentan las herramientas del cálculo, como la regla de la suma, del producto y la cadena, destacando su relevancia en la comprensión de fenómenos complejos y su uso en la ciencia moderna.

Takeaways

• 😀 El cálculo diferencial es una herramienta matemática fundamental para analizar el cambio en las cosas, y su poder reside en la derivada.
• 😀 La armonía pitagórica, descubierta hace más de 600 años, representa la primera relación entre las matemáticas y el mundo físico.
• 😀 Galileo Galilei destacó la importancia del lenguaje matemático para entender el universo, llamando a las matemáticas el lenguaje del universo.
• 😀 La derivada es el ritmo de cambio de cualquier función en un punto determinado y tiene aplicaciones en diversos campos, como la física y la música.
• 😀 El cálculo diferencial permitió a Galileo comprender el movimiento, pero se necesitaba un lenguaje más avanzado para expresar ideas complejas.
• 😀 Después de Galileo, surgió el cálculo diferencial como el lenguaje matemático que permitía describir el cambio y la aceleración en diversos fenómenos.
• 😀 La pendiente de una curva en un punto específico se puede aproximar usando el concepto de la tangente, que se obtiene al acercar dos puntos de la curva.
• 😀 El concepto de derivada se explica a través de ejemplos prácticos, como la caída de un cuerpo, la velocidad de un vehículo o el cambio en el precio de una pizza.
• 😀 Las reglas del cálculo diferencial, como la suma, el producto y la cadena, permiten descomponer funciones complejas en partes más sencillas para hallar su derivada.
• 😀 Albert Einstein, al estudiar la gravitación, expresó su respeto por las matemáticas, reconociendo su importancia para el avance de la física, aunque las matemáticas son vistas por los físicos como herramientas, no como un lujo.

Q & A

¿Qué es el cálculo diferencial y para qué se utiliza?

El cálculo diferencial es una herramienta matemática poderosa que se utiliza para analizar el cambio en las cosas, como la velocidad o el ritmo de variación de diferentes funciones en un punto específico.

¿Cómo se conecta el cálculo diferencial con la música?

El cálculo diferencial está relacionado con la música a través de la armonía pitagórica, que fue un descubrimiento que demostró cómo las matemáticas, específicamente las relaciones numéricas sencillas, explican los acordes musicales en instrumentos de cuerda.

¿Quiénes fueron los principales descubridores en la historia del cálculo diferencial?

Galileo Galilei, Pierre de Fermat y Isaac Newton fueron algunos de los principales personajes históricos que contribuyeron al desarrollo del cálculo diferencial. Galileo introdujo conceptos de cinemática, Fermat investigó las tangentes de curvas, y Newton formalizó el análisis matemático con el cálculo.

¿Qué contribución hizo Galileo al entendimiento de las matemáticas en el mundo físico?

Galileo unificó las matemáticas y el mundo físico al comprender que el universo estaba 'escrito' en el lenguaje de las matemáticas, y destacó la importancia de aprender este 'lenguaje' para poder entender la naturaleza.

¿Qué es una derivada en el contexto del cálculo diferencial?

Una derivada representa el ritmo de cambio de una función en un punto determinado. Se utiliza para medir cómo una cantidad varía en relación con otra, como la velocidad de un objeto en movimiento o la pendiente de una curva.

¿Cómo se puede calcular la pendiente de una curva en un punto específico?

La pendiente de una curva en un punto se calcula a través de la derivada, que se obtiene acercando un segundo punto a la recta tangente en el primero, y evaluando el valor límite de la pendiente de la línea secante cuando los puntos se aproximan.

¿Qué ejemplos se dan en el guion para ilustrar el concepto de derivada?

El guion menciona ejemplos como la velocidad instantánea de un objeto en movimiento, el cambio de temperatura en relación con la densidad de la población de delfines, o el ritmo de cambio en el precio de una pizza con respecto a su tamaño.

¿Qué es una tangente y cómo se relaciona con el concepto de derivada?

Una tangente es una recta que toca una curva en un punto sin cruzarla. La derivada de una función en ese punto es precisamente la pendiente de la recta tangente, que nos da el ritmo de cambio de la función en ese punto específico.

¿Cuáles son algunas de las reglas básicas para calcular derivadas?

Las reglas básicas incluyen la regla de la suma (la derivada de una suma es la suma de las derivadas), la regla del producto (que calcula la derivada del producto de dos funciones), y la regla de la cadena (que se usa cuando una función depende de otra función).

¿Cómo el cálculo diferencial es útil en la vida moderna?

El cálculo diferencial es fundamental en la vida moderna porque se aplica en herramientas y máquinas como velocímetros y odómetros, que miden la velocidad instantánea y el desplazamiento de objetos. También es esencial en la optimización de procesos en física, ingeniería y economía.