5.2: The Derivative as a Function, Part 2
Summary
TLDREste video profundiza en el concepto de la derivada en cálculo, explicando su función como la medida de la pendiente de una curva o la tasa de cambio instantánea en un punto específico. Se detallan las notaciones y el proceso de cálculo de derivadas, incluyendo el uso de límites. También se aborda la diferenciabilidad, destacando que una función debe ser continua para ser diferenciable. Se exploran aplicaciones prácticas, como la velocidad y la aceleración, y se explica cómo los derivados de orden superior se relacionan con el cambio de aceleración en situaciones como los movimientos de caída libre o montañas rusas.
Takeaways
- 😀 La derivada mide la pendiente de la curva en un punto o la tasa de cambio instantánea en ese punto.
- 😀 La derivada se define como el límite cuando H tiende a cero de un cociente de diferencias: (f(x+h) - f(x))/h.
- 😀 El símbolo de la derivada puede escribirse como f'(x), y'(x), o dy/dx, entre otros.
- 😀 Una función es diferenciable si tiene una derivada que existe en cada punto de su dominio.
- 😀 Si una función es diferenciable en un punto, debe ser continua en ese punto, pero la continuidad no garantiza diferenciabilidad.
- 😀 Las derivadas de funciones pueden usarse para determinar el comportamiento de la función en cualquier punto de su dominio.
- 😀 La derivada de una función de posición, como S(t), representa la velocidad, es decir, el cambio de la posición con respecto al tiempo.
- 😀 La segunda derivada de una función de posición, S''(t), representa la aceleración, o el cambio de velocidad con respecto al tiempo.
- 😀 En algunos casos, como en las montañas rusas, la derivada de la aceleración puede describir el ‘tirón’, que es el cambio en la aceleración a lo largo del tiempo.
- 😀 Cuando una función tiene una esquina o un vértice, como el valor absoluto, no es diferenciable en ese punto, aunque puede ser continua.
- 😀 Las derivadas de la derivada, como la segunda o tercera derivada, permiten analizar cambios en la velocidad, aceleración y otras tasas de cambio más complejas.
Q & A
¿Qué mide la derivada de una función?
-La derivada mide la pendiente de la curva en un punto específico o la tasa de cambio instantánea de la función en ese punto.
¿Cómo se define la derivada de una función en términos de un límite?
-La derivada se define como el límite cuando H tiende a cero de un cociente de diferencia: (f(x + h) - f(x)) / h.
¿Qué significa 'derivada' visualmente en términos de la gráfica de una función?
-La derivada representa la pendiente de la línea tangente a la curva en un punto específico. Esto se refiere a cómo cambia la función en ese punto.
¿Qué notación se usa comúnmente para representar la derivada?
-Se utilizan varias notaciones para la derivada, como f'(x), y'(x), dy/dx, o df/dx, dependiendo del contexto y la función que se esté considerando.
¿Qué significa que una función sea diferenciable?
-Una función es diferenciable si tiene una derivada en todos los puntos de un intervalo específico, lo que implica que la función es continua en ese intervalo.
¿En qué casos la derivada de una función no existe?
-La derivada no existe cuando la función tiene un ángulo agudo o un punto de inflexión (esquinas, cúspides o tangentes verticales).
¿Cómo se relaciona la continuidad de una función con su diferenciabilidad?
-Para que una función sea diferenciable en un punto, debe ser continua en ese mismo punto. Sin embargo, una función continua no siempre es diferenciable.
¿Qué sucede en el punto donde la función absoluta tiene un cambio de dirección?
-En el caso de la función valor absoluto, la derivada no existe en el punto donde cambia de dirección, ya que presenta una esquina, lo que impide la existencia de una derivada en ese punto.
¿Qué es la segunda derivada y qué representa?
-La segunda derivada es la derivada de la primera derivada y representa la tasa de cambio de la pendiente de la curva, a menudo relacionada con la aceleración en aplicaciones físicas.
¿Cómo se interpreta la tercera derivada en términos de la aceleración?
-La tercera derivada describe cómo cambia la aceleración con el tiempo. En el caso de un paseo en montaña rusa, por ejemplo, se refiere al cambio de la aceleración que el cuerpo experimenta debido a los movimientos de la montaña rusa.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
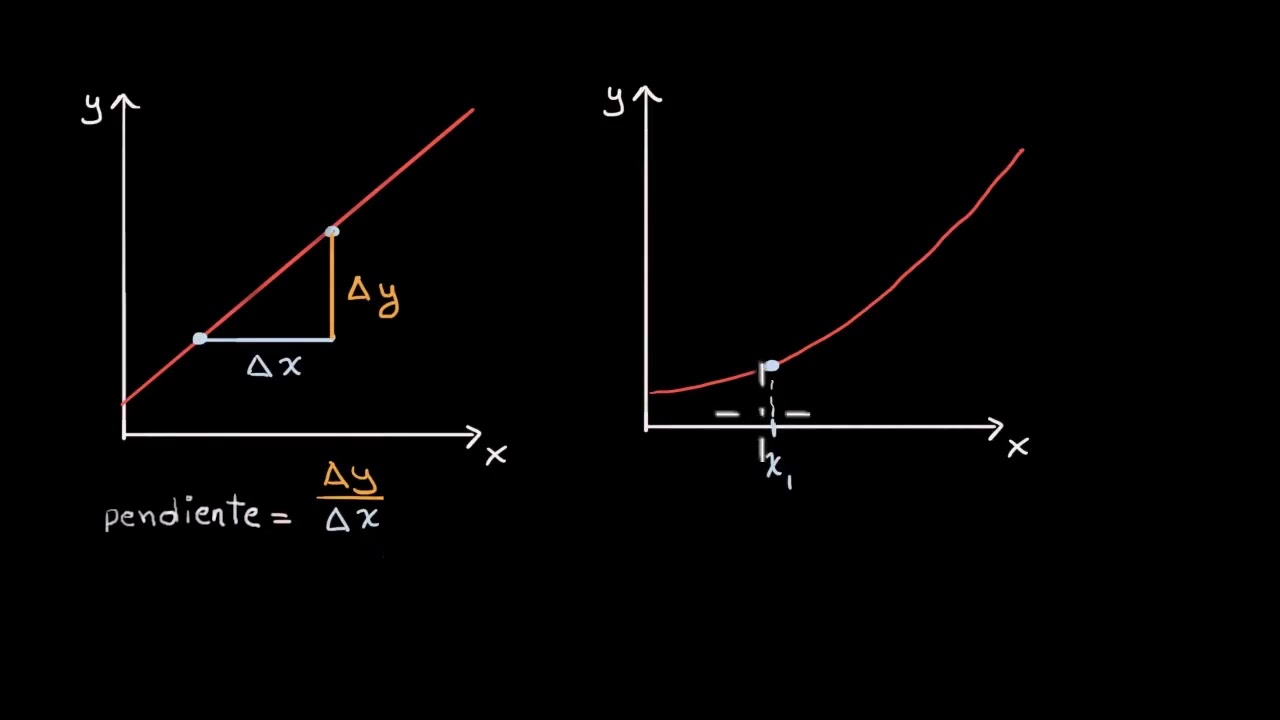
El concepto de derivada | Khan Academy en Español

INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA, CÁLCULO DIFERENCIAL

QUÉ ES EL CÁLCULO DIFERENCIAL. Explicación Básica.

¿Qué es la derivada? Idea intuitiva

¿Qué es la derivada? El concepto gráfico de derivada. ¿Qué es doblegar la curva?

El concepto de derivada. ¿Qué es y para qué sirve la derivada?
5.0 / 5 (0 votes)
