Edging in Math - Morgan Freeman and Jake Paul explain taking Limits
Summary
TLDRIn this casual yet informative video, the concept of limits in calculus is explained with relatable examples. The host breaks down how limits describe the value a function approaches as the input gets closer to a specific number, without actually reaching it. Using a simple linear function and a more complex fraction, the video clarifies how to handle limits, including cases of indeterminate forms like 0/0. The video keeps a light tone, making a potentially tricky topic more accessible and engaging for learners.
Takeaways
- 😀 A limit describes the value a function approaches as X gets close to a specific number, without actually reaching it.
- 😀 To visualize a limit, look at how a function behaves as X approaches a number from both the left and the right sides.
- 😀 If both sides of the function approach the same value, that value is the limit of the function at that point.
- 😀 In the example with 2x + 1, as X approaches 2, both the left and right side approach the value 5, so the limit is 5.
- 😀 Plugging in the number directly (like X = 2) works for some functions, but this approach might not work in all cases.
- 😀 Some functions, especially with fractions, may have points where direct substitution leads to undefined values (like 0/0).
- 😀 When a function has a fraction with 0/0, this suggests a gap or hole in the graph at that specific value of X.
- 😀 Even if there’s a gap at X = 3 (in the fraction example), the limit can still exist if the function approaches the same value from both sides.
- 😀 In the case of the fraction example, the function approaches the value 1 as X gets closer to 3, so the limit as X approaches 3 is 1.
- 😀 Taking the limit is about approaching a value as closely as possible without actually stepping over it, focusing on the behavior near the point of interest.
Q & A
What is a limit in mathematics?
-A limit is essentially the value that a function approaches as the input (X) gets closer and closer to a specific number, without actually reaching it.
Can you explain how to visualize a limit on a graph?
-To visualize a limit on a graph, you observe what happens as X approaches a specific value from both the left and the right. If both sides converge to the same value, that is the limit.
What does it mean if the limit of a function is 5?
-If the limit is 5, it means that as X approaches a certain value, the function's value gets closer to 5 from both sides, even if it never actually reaches it at that point.
Can the limit always be found by plugging in the value of X directly?
-Not always. In some cases, especially when the function has a gap or undefined value at that point, you can't simply plug in X. Instead, you need to analyze how the function behaves as X approaches that value.
What happens if a function has a gap at a specific X value?
-If there is a gap at a specific X value, the limit still exists if the function approaches the same value from both sides, even though the function is not defined at that exact point.
How does the fraction example in the script illustrate the concept of limits?
-In the fraction example, even though the function is undefined at X=3 (because it leads to a 0/0 situation), the limit as X approaches 3 is 1, since the function values from both sides approach 1.
What does it mean when a fraction simplifies to 1?
-When a fraction simplifies to 1, it means that the numerator and denominator are identical (except possibly at certain points), so the function approaches a value of 1 as X gets closer to the specific value.
What is meant by the phrase 'edging' in the context of limits?
-In the context of limits, 'edging' refers to approaching the value of X as closely as possible from either direction without actually stepping over or reaching that value.
Why is 0/0 an undefined value in mathematics?
-0/0 is undefined because division by zero is not allowed in mathematics. It leads to indeterminate results, which is why the limit process is needed to understand the behavior of the function near that point.
How do you find a limit when a function has a gap?
-To find the limit when a function has a gap, you look at the behavior of the function as X approaches the point from both the left and the right. If both approaches lead to the same value, that is the limit, even if there's a gap at that point.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)

Calculus - Introduction to Calculus

Limit Fungsi Tak Hingga

Limit of a Function using a Graph - Basic/Differential Calculus
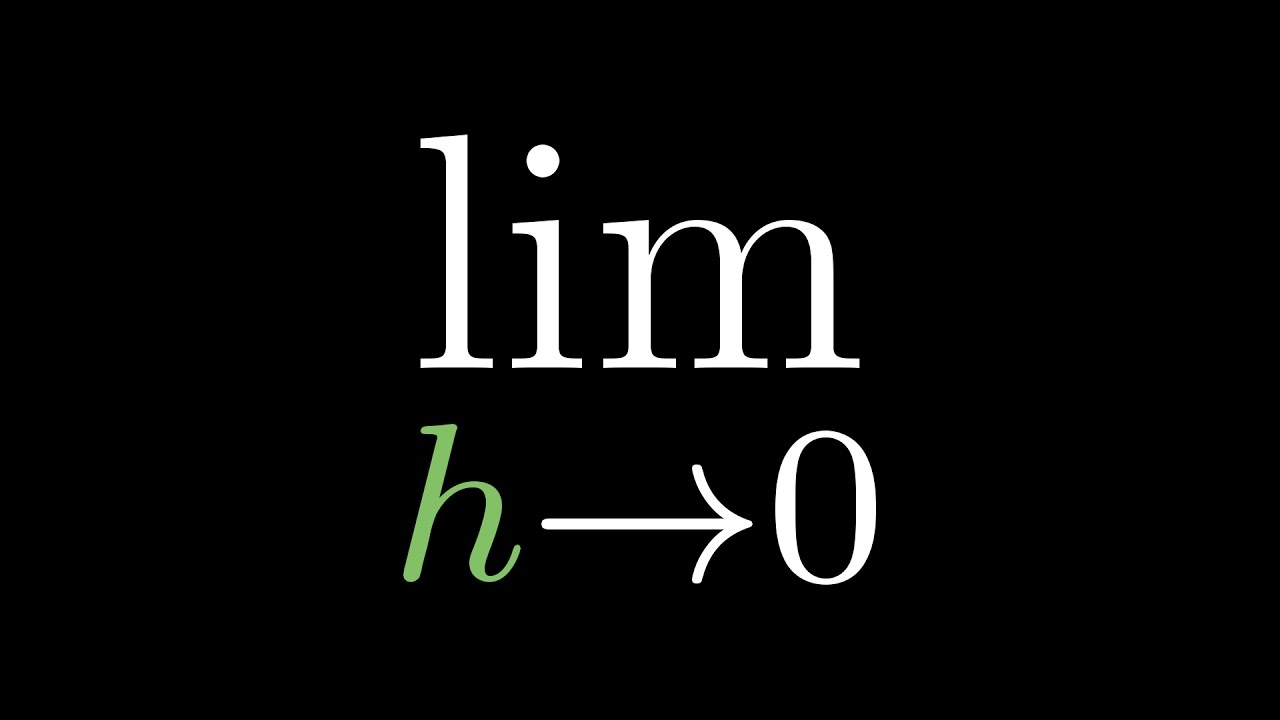
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

KALKULUS INTEGRAL - INTEGRAL TAK WAJAR
5.0 / 5 (0 votes)
