Problema 2 de MEZCLA
Summary
TLDREn este video, se resuelve un problema de mezclas donde se deben combinar dos soluciones de alcohol con concentraciones del 30% y 70% para obtener una mezcla con una concentración del 60%. Se utiliza una ecuación de balance de masas, donde se plantean las cantidades y concentraciones de cada solución. A través de los pasos de simplificación y resolución de la ecuación, se determina que se deben usar 30 litros de la solución al 30%. El video proporciona una explicación detallada de cómo resolver este tipo de problemas de mezclas de manera clara y comprensible.
Takeaways
- 😀 Se trata de un problema de mezcla de soluciones con diferentes concentraciones de alcohol.
- 😀 El objetivo es encontrar cuántos litros de una solución al 30% deben mezclarse con 90 litros de una solución al 70% para obtener una mezcla al 60%.
- 😀 La fórmula utilizada para resolver el problema es: cantidad1 * concentración1 + cantidad2 * concentración2 = cantidad mezcla * concentración mezcla.
- 😀 La incógnita en este problema es la cantidad de la solución al 30%, representada por 'x' litros.
- 😀 La ecuación planteada para resolver el problema es: x * 0.30 + 90 * 0.70 = (x + 90) * 0.60.
- 😀 El valor de 'x' representa la cantidad de la solución al 30% que debe mezclarse con la solución al 70%.
- 😀 Al resolver la ecuación, se obtiene x = 30, lo que significa que deben usarse 30 litros de la solución al 30%.
- 😀 El proceso de resolución implica despejar términos y aplicar la propiedad distributiva para simplificar la ecuación.
- 😀 La transposición de términos y la reducción de términos semejantes son pasos clave en la resolución de la ecuación.
- 😀 Finalmente, la respuesta a la pregunta es que se deben utilizar 30 litros de la solución de alcohol al 30% para obtener la mezcla deseada al 60%.
Q & A
¿Qué tipo de problema se está resolviendo en el video?
-Se está resolviendo un problema de mezclas de soluciones con diferentes concentraciones de alcohol.
¿Cuál es la fórmula que se utiliza para resolver el problema?
-La fórmula utilizada es: cantidad1 * concentración1 + cantidad2 * concentración2 = cantidad mezcla * concentración mezcla.
¿Qué representan los valores 'x' y '90' en la ecuación planteada?
-'x' representa la cantidad de litros de la solución al 30% que se deben mezclar, y '90' representa la cantidad de litros de la solución al 70%.
¿Cómo se determina la cantidad total de la mezcla?
-La cantidad total de la mezcla es la suma de las cantidades de ambas soluciones: 'x' litros de alcohol al 30% y 90 litros de alcohol al 70%.
¿Qué significa el 60% en la ecuación?
-El 60% es la concentración deseada de la mezcla final de alcohol después de mezclar las dos soluciones.
¿Qué se hace después de escribir la ecuación con todos los valores?
-Después de escribir la ecuación, se aplican las operaciones aritméticas, como la propiedad distributiva y la transposición de términos para despejar la incógnita 'x'.
¿Qué operación se realiza para simplificar la ecuación?
-Se realizan operaciones de multiplicación y luego transposición de términos para dejar todos los términos con 'x' en un lado y los números en el otro lado de la ecuación.
¿Qué sucede al resolver la ecuación?
-Al resolver la ecuación, se encuentra que el valor de 'x' es 30, lo que significa que se deben utilizar 30 litros de la solución de alcohol al 30%.
¿Cuál es el valor final de 'x' y qué implica?
-El valor final de 'x' es 30, lo que implica que se deben mezclar 30 litros de la solución al 30% con 90 litros de la solución al 70% para obtener una mezcla al 60%.
¿Cómo se verifica el resultado de la ecuación?
-El resultado se verifica sustituyendo el valor de 'x' en la ecuación original y comprobando que ambas partes de la igualdad sean iguales.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Concentración de las soluciones - %mm - Lección

Función Racional - Ejercicios Nivel 3 - Aplicaciones

[ QUIMICA FREE ] - SOLUCIONES II - Molaridad - Normalidad - Mezcla de soluciones

diluciones
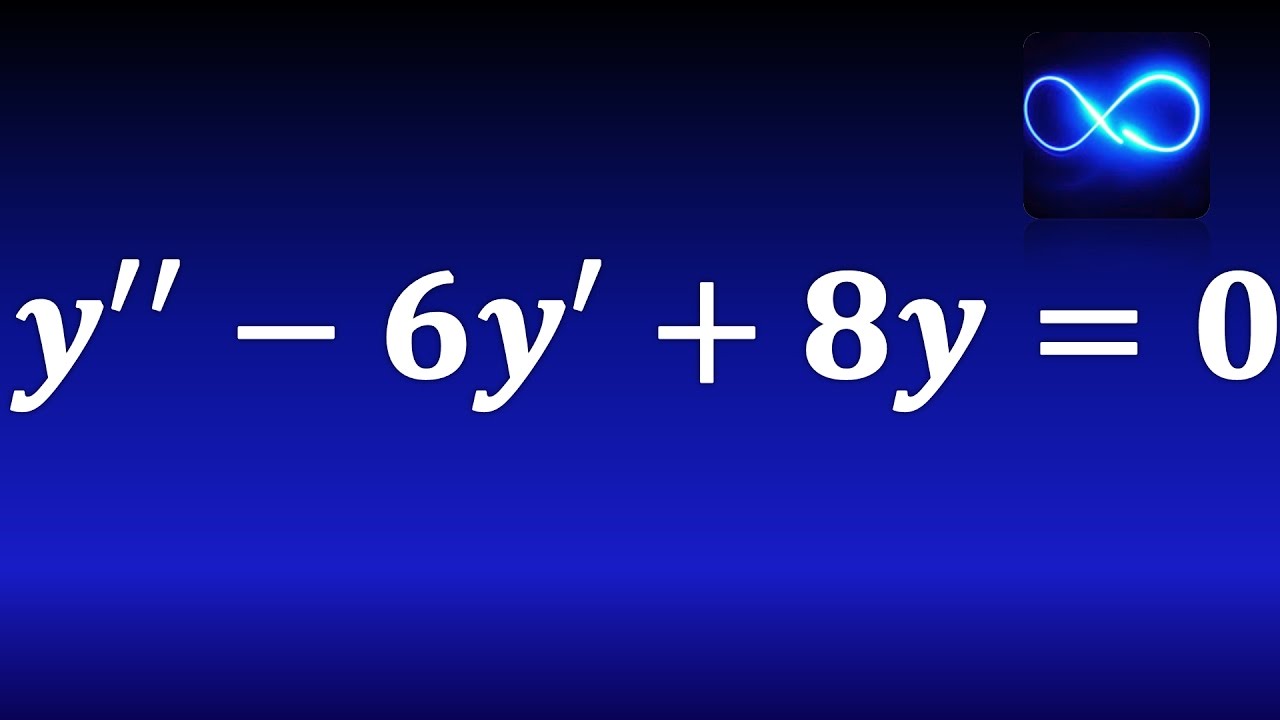
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

COMO CALCULAR LA CONCENTRACIÓN DE UNA SOLUCIÓN. %m/m, %v/v, %m/v. SOLUCIONES 3. QUÍMICA CON IRWIN
5.0 / 5 (0 votes)
