Solving Systems of Equations By Graphing
Summary
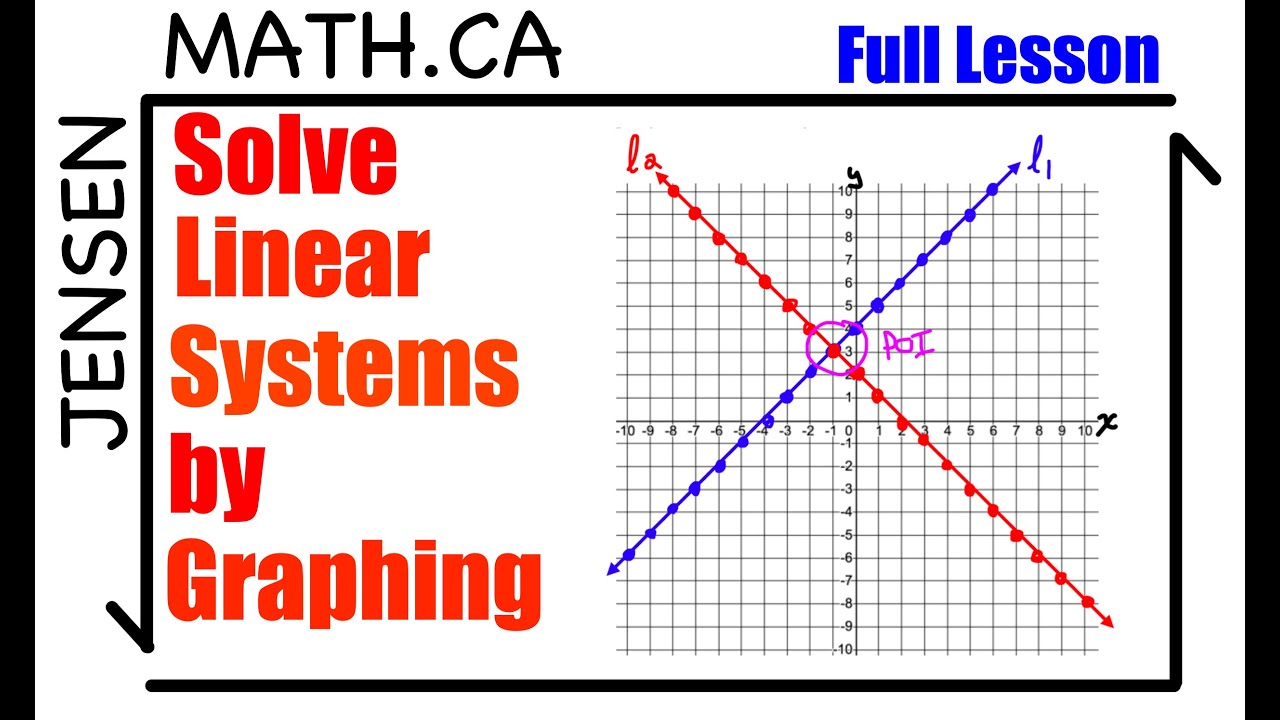
TLDRIn this lesson, the instructor demonstrates how to solve a system of equations by graphing. The equations y = 2x - 3 and y = -2/3x + 5 are graphed to identify their point of intersection, which is the solution to the system. The instructor emphasizes the importance of using a large graph for clarity and walks through the process of finding key points based on the slope and y-intercept. Additionally, the solution is verified through substitution, confirming that the intersection point is (3, 3). This comprehensive approach reinforces both graphical and algebraic methods for solving equations.
Takeaways
- 📊 Graphing is an effective method for solving systems of equations.
- 📏 The first equation given is in slope-intercept form: y = 2x - 3.
- 🔍 The slope of the first equation is 2, and the y-intercept is -3.
- ⬆️ To plot the first equation, start at the y-intercept and use the slope to find additional points.
- 📈 The second equation is y = -2/3x + 5, which also follows slope-intercept form.
- 🎯 The y-intercept of the second equation is 5, with a slope of -2/3.
- 🗺️ Finding the point of intersection of the two graphs provides the solution to the system of equations.
- ✅ The point of intersection determined through graphing is (3, 3).
- 🔄 Substitution is another method to solve for the intersection of the equations.
- ✖️ Eliminating fractions in equations can simplify the solving process.
Q & A
What are the two equations being solved in this lesson?
-The two equations are y = 2x - 3 and y = -2/3x + 5.
How do you determine the point of intersection when graphing two equations?
-The point of intersection is found by graphing both equations on a coordinate plane and identifying where the two lines cross.
What is the slope of the first equation, and how is it used?
-The slope of the first equation (y = 2x - 3) is 2, which indicates that for every 1 unit you move to the right on the x-axis, you move up 2 units on the y-axis.
What is the significance of the y-intercept in these equations?
-The y-intercept indicates where the line crosses the y-axis. For the first equation, the y-intercept is -3, meaning it starts at the point (0, -3) on the graph.
How do you graph the second equation?
-To graph the second equation (y = -2/3x + 5), start at the y-intercept of 5 on the y-axis, then use the slope of -2/3 to find additional points by moving 3 units right and 2 units down.
What is the calculated point of intersection for these equations?
-The calculated point of intersection for the two equations is (3, 3).
What method is used to verify the solution after graphing?
-The solution is verified using substitution by replacing y in one equation with the expression from the other equation and solving for x.
How do you eliminate fractions when solving the equation?
-You can eliminate fractions by multiplying every term in the equation by a common denominator, which simplifies the calculations.
What does the result x = 3 indicate in the context of the equations?
-The result x = 3 indicates the x-coordinate of the point of intersection, which is used to find the corresponding y-coordinate.
Why is it beneficial to draw a larger graph?
-Drawing a larger graph allows for better visualization of the intersection point and makes it easier to plot points accurately.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

SOLVING SYSYEM OF NONLINEAR EQUATIONS || PRECALCULUS
Solve a Linear System by Graphing | jensenmath.ca | grade 10

SPLTV Kelas 10 Kurikulum Merdeka

MaTek 1 Menggambar grafik Fungsi Linier #Part 6#Matematika Teknik 1

PERSAMAAN KUADRAT part ZERO-ONE

Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel
5.0 / 5 (0 votes)
