Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Summary
TLDRThis video explains the fundamental concepts of trigonometric functions using the unit circle. It illustrates how the sine and cosine of an angle are represented by the vertical and horizontal distances on the circle, respectively. The tangent, secant, cotangent, and cosecant are derived from the properties of similar triangles. Key relationships such as the Pythagorean identities are highlighted, emphasizing the interconnectedness of these functions. The video also notes that sine and cosine values range between -1 and 1, while tangent and cotangent can extend to infinity. Overall, it provides a visual and conceptual understanding of trigonometric relationships.
Takeaways
- 😀 A unit circle with a radius of 1 helps visualize trigonometric functions.
- 🟢 The sine of an angle theta corresponds to the vertical distance from the x-axis on the unit circle.
- 🔵 The cosine of an angle theta corresponds to the horizontal distance from the y-axis on the unit circle.
- 🔺 The coordinates of a point on the unit circle are (cosine(theta), sine(theta)).
- 📏 The tangent of theta is defined as sine(theta) divided by cosine(theta).
- 🔁 The secant of theta is defined as 1 divided by cosine(theta).
- ↔️ The cotangent of theta is defined as cosine(theta) divided by sine(theta).
- 💡 The cosecant of theta is defined as 1 divided by sine(theta).
- 🚫 The tangent and secant functions become undefined at pi/2 radians.
- 📐 The Pythagorean theorem leads to key trigonometric identities: sine²(theta) + cosine²(theta) = 1.
Q & A
What is the unit circle, and how is it used in trigonometry?
-The unit circle is a circle with a radius of 1, used to define trigonometric functions. The coordinates of points on the unit circle are represented as (cosine, sine) of an angle, which helps in understanding the relationships between sine, cosine, and other trigonometric functions.
What does the sine of an angle represent on the unit circle?
-The sine of an angle, represented as sin(θ), is the vertical distance from the point on the unit circle to the x-axis.
What does the cosine of an angle represent on the unit circle?
-The cosine of an angle, represented as cos(θ), is the horizontal distance from the point on the unit circle to the y-axis.
What are the coordinates of a point on the unit circle for an angle θ?
-The coordinates of a point on the unit circle for an angle θ are given by (cos(θ), sin(θ)).
How are the tangent and secant functions defined in relation to the unit circle?
-The tangent of an angle θ is defined as the ratio of the sine to the cosine, or tan(θ) = sin(θ)/cos(θ). The secant of θ is the reciprocal of the cosine, defined as sec(θ) = 1/cos(θ).
What are cotangent and cosecant, and how are they related to the unit circle?
-The cotangent of an angle θ is defined as the ratio of the cosine to the sine, or cot(θ) = cos(θ)/sin(θ). The cosecant of θ is the reciprocal of the sine, defined as csc(θ) = 1/sin(θ).
Why are tangent and secant undefined at certain angles?
-Tangent and secant are undefined at angles where the cosine of the angle is zero, such as θ = π/2, because you cannot divide by zero.
What do the values of sine and cosine range between?
-The values of sine and cosine range between -1 and 1, as they represent lengths that cannot extend beyond the unit circle with a radius of 1.
What does the Pythagorean theorem reveal about trigonometric functions?
-The Pythagorean theorem leads to important identities in trigonometry, such as sin²(θ) + cos²(θ) = 1, which relates the sine and cosine of an angle.
How are the relationships between tangent, secant, cotangent, and cosecant expressed using triangles?
-The relationships are expressed through triangle similarity, leading to identities like 1 + tan²(θ) = sec²(θ) and 1 + cot²(θ) = csc²(θ). These identities highlight the connection between the functions and the properties of right triangles.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
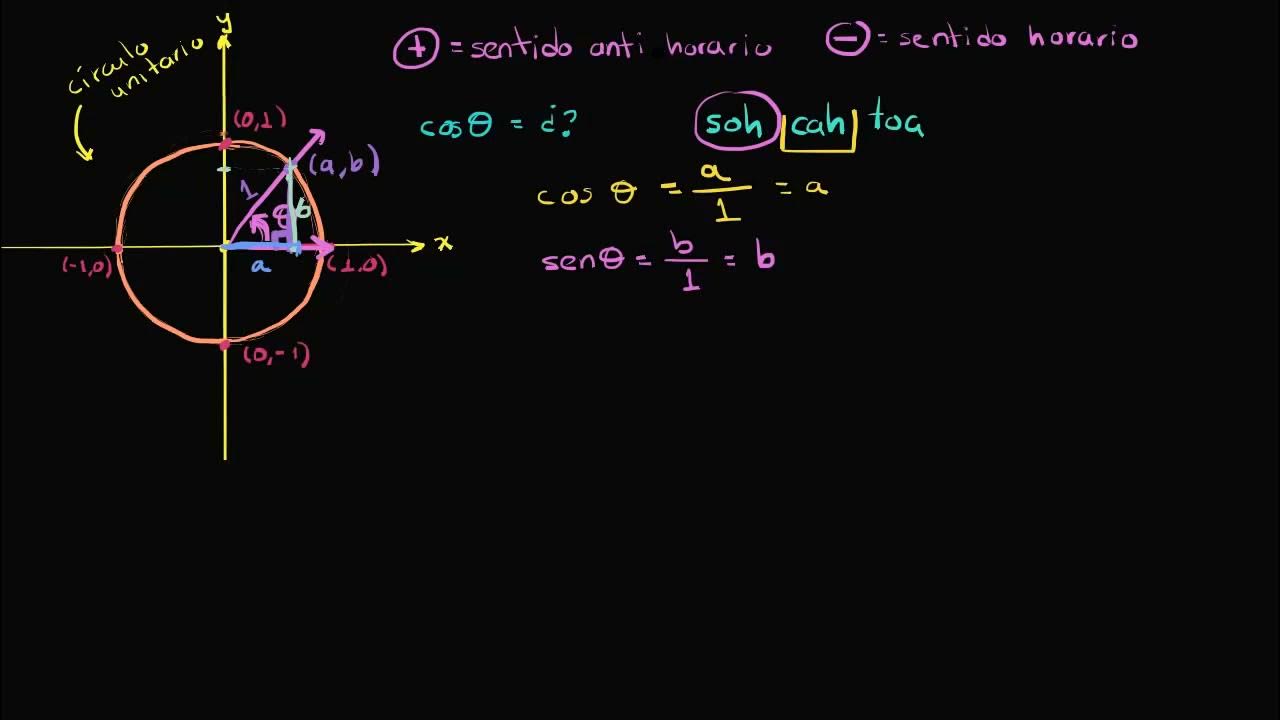
Círculo unitario. Definición de funciones trigonométricas

Stop memorizing the unit circle

De eenheidscirkel (HAVO wiskunde B)

Tanda Fungsi Trigonometri Tiap Kuadran | Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
Trigonometri Matematika Kelas 10 • Part 32: Menggambar Grafik Fungsi y=cos x dengan Lingkaran Satuan
Introduction to the unit circle | Trigonometry | Khan Academy
5.0 / 5 (0 votes)
