Standing waves in closed tubes | Mechanical waves and sound | Physics | Khan Academy
Summary
TLDRThis educational video script explores the physics of sound waves in tubes, contrasting open-open and open-closed configurations. It explains how only specific wavelengths are allowed in open-open tubes due to anti-nodes at both ends, while open-closed tubes, akin to a soda bottle, exhibit different behavior with nodes at the closed end and anti-nodes at the open end. The script derives formulas for possible wavelengths in these tubes, highlighting that open-closed tubes only support odd harmonics. It concludes with a practical demonstration using a soda bottle to illustrate how the pitch changes as the liquid level decreases, reflecting the inverse relationship between tube length and frequency.
Takeaways
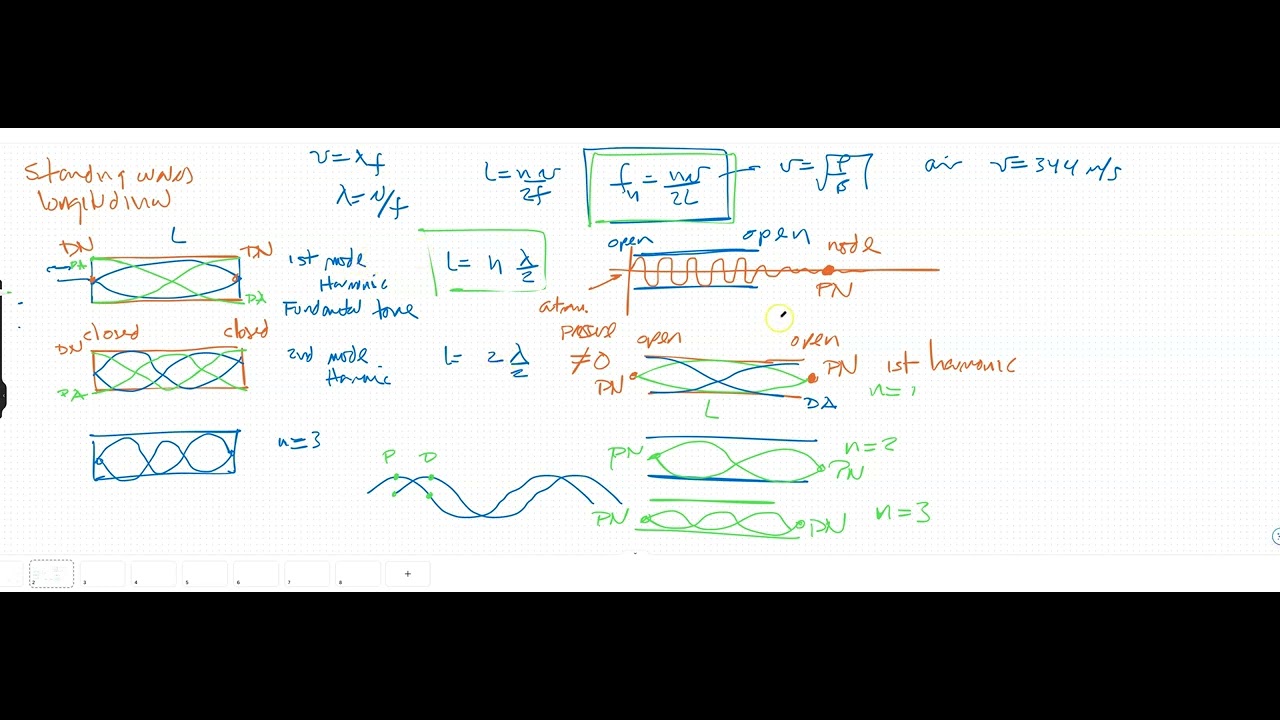
- 🎵 In an open-open tube, only specific wavelengths are allowed due to the requirement for anti-nodes at both ends.
- 🌌 The possible wavelengths in an open-open tube can be calculated using a formula involving the tube's length (L) and the harmonic number (N).
- 🚫 When one end of the tube is closed, the conditions change, leading to different possible wavelengths.
- 🔄 A closed end of a tube creates a node, where air molecules cannot oscillate, unlike an open end which is an anti-node.
- 📏 The fundamental wavelength for an open-closed tube is four times the length of the tube (L), compared to two times the length for an open-open tube.
- 🎶 The wavelengths in an open-closed tube are given by the formula \( \lambda = \frac{4L}{N} \), where N must be an odd integer (1, 3, 5, ...).
- 🚫 Even harmonics are not present in an open-closed tube; only odd harmonics are allowed due to the node at the closed end.
- 🌉 The relationship between the length of the tube and the wavelength affects the frequency heard, with longer tubes producing lower frequencies.
- 🥤 An everyday example given is drinking from a soda bottle, where the length of the 'tube' (from the open top to the liquid level) changes as the liquid is consumed, altering the pitch of the sound produced.
- 📉 As the length of the tube increases (more liquid is drunk), the wavelength increases and the frequency decreases, resulting in a lower pitch or note.
Q & A
What are the conditions for the formation of standing waves in an open-open tube?
-In an open-open tube, standing waves can only form at specific wavelengths where anti-nodes are present at both ends of the tube.
How does the wavelength formula for an open-open tube relate to the tube's length and harmonic number?
-The formula for the wavelength in an open-open tube is \(\lambda = 2L\) for the fundamental frequency, where \(L\) is the length of the tube and \(N\) is the harmonic number (1 for the fundamental, 2 for the second harmonic, and so on).
What happens to the possible wavelengths when one end of the tube is closed?
-When one end of the tube is closed, the possible wavelengths change because a node is required at the closed end, leading to different standing wave patterns.
How does the closed end affect the type of node at that end of the tube?
-At the closed end of the tube, the air molecules cannot oscillate, resulting in a node, as there can't be any displacement at this point.
What is the fundamental wavelength for an open-closed tube?
-The fundamental wavelength for an open-closed tube is \(\lambda = 4L\), where \(L\) is the length of the tube.
What is the relationship between the wavelength and the tube length for the first few harmonics in an open-closed tube?
-For the first few harmonics in an open-closed tube, the wavelengths are \(\lambda = 4L\) (fundamental), \(\lambda = \frac{4L}{3}\) (third harmonic), \(\lambda = \frac{4L}{5}\) (fifth harmonic), and so on, with only odd harmonics being allowed.
Why are only odd harmonics present in an open-closed tube?
-Only odd harmonics are present in an open-closed tube because the closed end requires a node, and the open end requires an anti-node, which results in the exclusion of even harmonics.
How can you experimentally verify the relationship between tube length and the frequency of sound produced?
-You can experimentally verify this by observing the change in pitch as you drink from a soda bottle and blow over the top, which changes the effective length of the tube and thus the wavelength and frequency of the sound produced.
What is the effect of increasing the length of the tube on the frequency of the sound produced?
-Increasing the length of the tube results in a larger wavelength and a lower frequency, producing a lower pitch sound.
How does the presence of ice in a drink affect the speed of sound and consequently the pitch?
-The presence of ice in a drink can slightly affect the speed of sound due to the change in the medium's temperature. However, as the ice melts, the pitch may change as the speed of sound in water is different from that in air.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Longitudinal standingg waves
Fisika Kelas 11 - PIPA ORGANA Terbuka dan Tertutup

Gelombang Bunyi • Part 3: Sumber Bunyi (Dawai, Pipa Organa Terbuka dan Tertutup)

FISIKA KELAS XI - GELOMBANG (PART 3) | Gelombang Stasioner Ujung Tertutup dan Ujung Terbuka

Open vs Closed Prompts Demonstrated in ChatGPT [ Discussion ]

Bentuk software : Open Source dan Close Source Software
5.0 / 5 (0 votes)
