Derivatives of inverse functions | Advanced derivatives | AP Calculus AB | Khan Academy
Summary
TLDRThe video explains the relationship between a function and its inverse, particularly focusing on their derivatives. Using the chain rule, the instructor derives a formula connecting the derivative of a function to the derivative of its inverse. By applying this concept to specific functions like \( e^x \) and its inverse, the natural log, the video demonstrates how this relationship holds true. This technique offers a useful method for calculating the derivative of an inverse function. The video encourages viewers to review inverse functions and apply calculus concepts for deeper understanding.
Takeaways
- 🧮 Inverse functions have the property that g(f(x)) = x, where g(x) is the inverse of f(x).
- 🔄 If f maps x to a value f(x), then the inverse function g takes f(x) back to x.
- 📝 The chain rule can be applied to find the derivative of inverse functions.
- 📉 Taking the derivative of both sides of g(f(x)) = x results in a useful relationship between the derivatives of a function and its inverse.
- ⚙️ Using the chain rule, we find that f'(x) = 1 / g'(f(x)).
- 🔍 This equation provides a link between the derivative of a function and the derivative of its inverse.
- 📚 For example, when f(x) = e^x, its inverse is g(x) = ln(x).
- 💡 The derivative of e^x is e^x, and the derivative of ln(x) is 1/x, supporting the derived relationship.
- 🔄 The formula holds true for other functions as well, verifying the relationship between inverse functions and their derivatives.
- 🧠 This concept helps in understanding and computing the derivative of an inverse function more efficiently.
Q & A
What is the relationship between two functions that are inverses of each other?
-If f(x) and g(x) are inverse functions, then applying g to f(x) (or f inverse of f(x)) results in x, meaning g(f(x)) = x.
How do inverse functions map values?
-An inverse function g maps the output of f(x) back to the original input x. If f(x) takes x to f(x), then g(f(x)) brings it back to x.
What rule is applied to find the derivative of inverse functions?
-The chain rule is applied to find the derivative of inverse functions, leading to a relationship between the derivatives of a function and its inverse.
How do you express the relationship between the derivatives of inverse functions?
-The derivative of f(x), f'(x), is equal to 1 divided by the derivative of g at f(x), or f'(x) = 1 / g'(f(x)).
Why is the relationship between the derivatives of inverse functions useful?
-This relationship allows you to calculate the derivative of an inverse function if you know the derivative of the original function.
What happens when you differentiate the equation g(f(x)) = x using the chain rule?
-Using the chain rule, the derivative of g(f(x)) = x results in g'(f(x)) * f'(x) = 1, which helps derive the formula f'(x) = 1 / g'(f(x)).
How can you verify the derivative relationship for exponential and logarithmic functions?
-For f(x) = e^x and g(x) = ln(x), f'(x) = e^x and g'(x) = 1/x. Substituting into the formula f'(x) = 1 / g'(f(x)) confirms the result.
What is the derivative of e^x, and why is it significant?
-The derivative of e^x is e^x itself, which is a unique and important result in calculus because the function equals its own derivative.
What is the derivative of the natural logarithm function?
-The derivative of the natural logarithm function ln(x) is 1/x.
Can you use the derivative relationship to find the derivative of inverse functions without directly differentiating them?
-Yes, using the relationship f'(x) = 1 / g'(f(x)), you can deduce the derivative of an inverse function by knowing the derivative of the original function.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
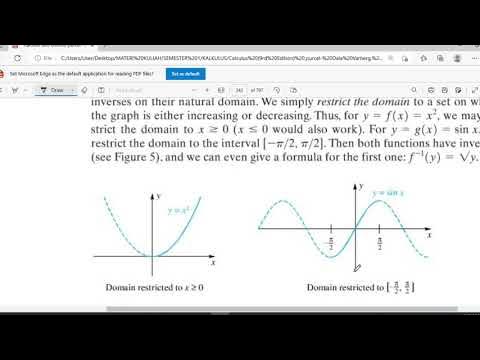
Fungsi Transenden 2 (Invers Fungsi dan Turunannya)

📚 Derivada - Definição e Cálculo - Cálculo 1 (#16)

FUNGSI INVERS KELAS 11, KONSEP DAN CONTOH SOAL mudah dipahami

Matematika Teknik I: 101 Fungsi Logaritma Natural - Definisi ln x dan turunannya
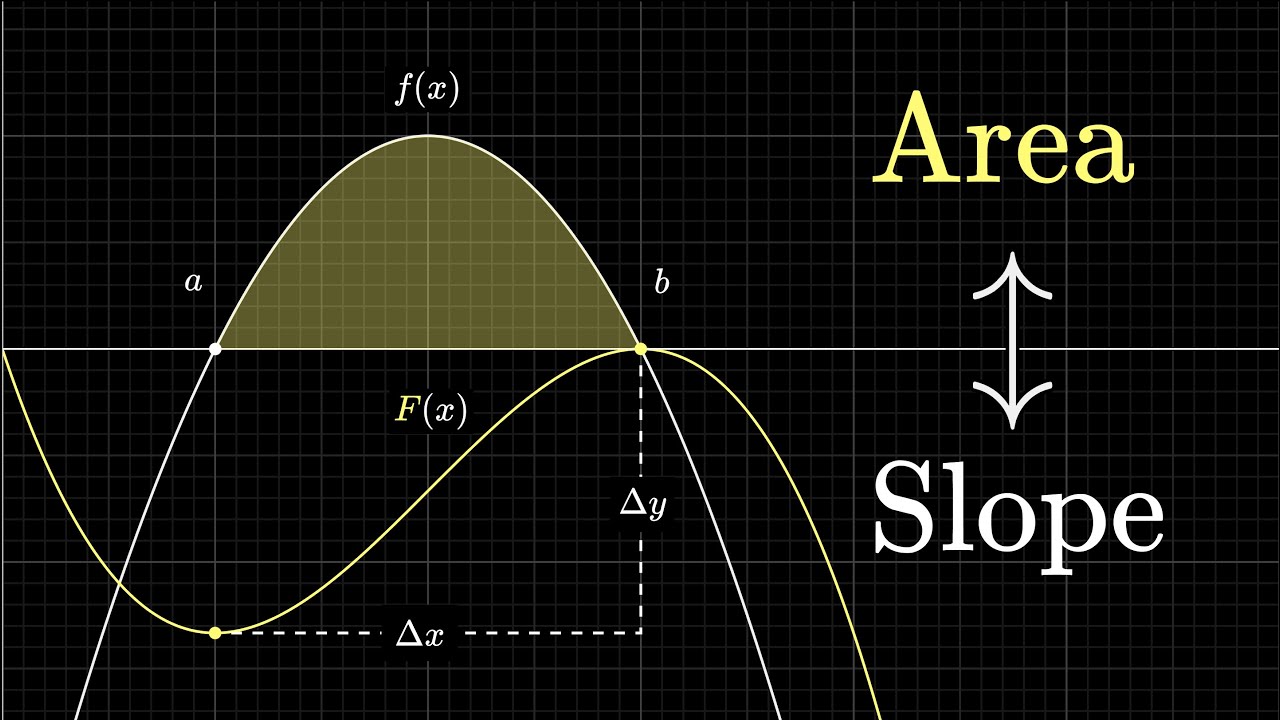
What does area have to do with slope? | Chapter 9, Essence of calculus
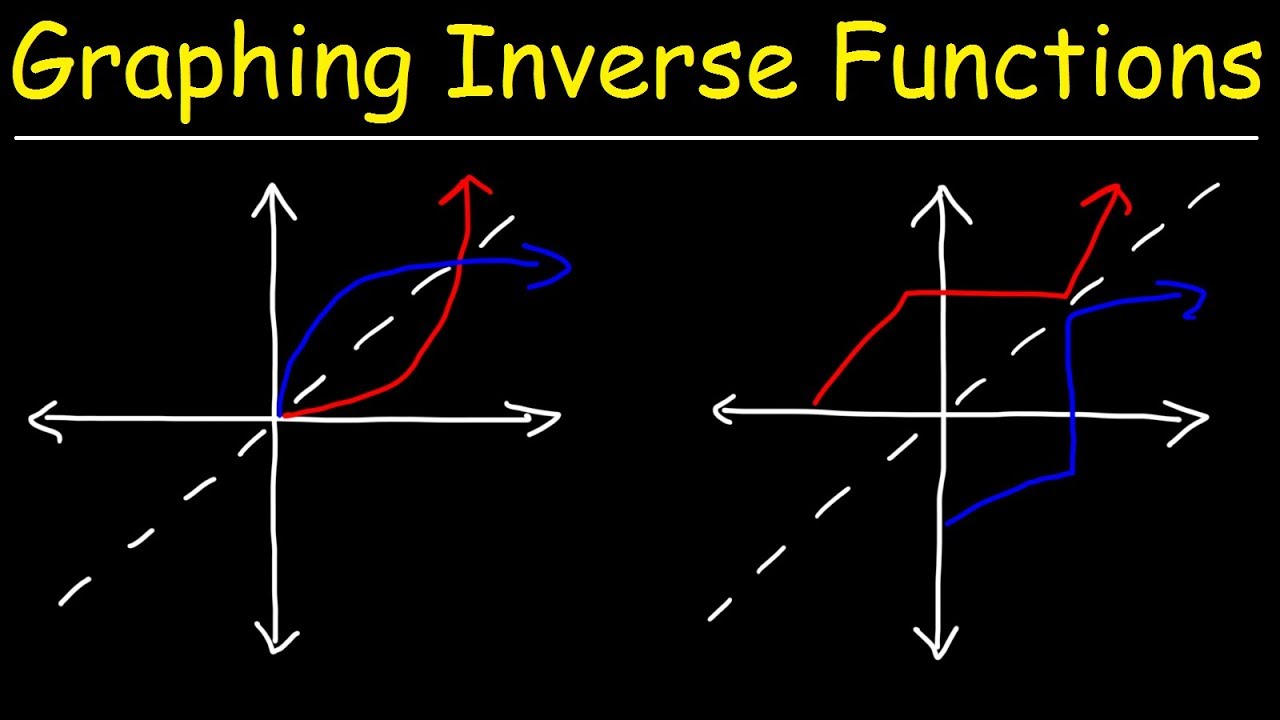
Graphing Inverse Functions
5.0 / 5 (0 votes)
