86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
Summary
TLDREn este vídeo tutorial de 'Mate, Fácil', se resuelve una ecuación diferencial lineal de segundo orden con coeficientes constantes. Se propone una solución de tipo exponencial, ya que las funciones exponenciales tienen derivadas que son ellas mismas. Se calculan las derivadas primera y segunda, y se sustituyen en la ecuación para obtener una ecuación característica. Se resuelve esta ecuación para encontrar los valores de 'r', que permiten obtener dos soluciones linealmente independientes. Finalmente, se combina estas soluciones con constantes arbitrarias para obtener la solución general de la ecuación diferencial.
Takeaways
- 📘 Para resolver una ecuación diferencial lineal de segundo orden con coeficientes constantes, se propone una solución de tipo exponencial.
- 🔍 Las funciones exponenciales son elegidas porque sus derivadas son ellas mismas, lo cual se alinea con la estructura de la ecuación diferencial.
- ✏️ Se calculan las primeras y segundas derivadas de la función exponencial propuesta para sustituir en la ecuación diferencial original.
- 🧮 Al sustituir las derivadas en la ecuación, se obtiene una ecuación que relaciona a r (la base de la exponencial) con una ecuación de segundo grado.
- 🔑 Se factoriza la ecuación resultante para encontrar los valores de r que satisfacen la ecuación, resultando en dos posibles valores para r.
- 📐 Los valores de r determinan las soluciones exponenciales individuales, que son linealmente independientes.
- 🌐 La solución general de la ecuación diferencial se obtiene combinando las soluciones individuales, multiplicadas por constantes arbitrarias.
- 🔄 Se menciona que se puede evitar el proceso de cálculo paso a paso y directamente resolver la ecuación característica para encontrar los valores de r.
- 📚 La ecuación característica tiene la misma forma que la ecuación diferencial, pero en términos de r, y se puede resolver para encontrar directamente las soluciones.
- 🔮 Se destaca que existen diferentes casos en ecuaciones de segundo grado, incluyendo soluciones reales duplicadas, una solución real única, o soluciones complejas.
Q & A
¿Qué tipo de ecuación diferencial se resuelve en el vídeo?
-Se resuelve una ecuación diferencial lineal de segundo orden con coeficientes constantes.
¿Cuál es la forma general de la ecuación diferencial que se resuelve en el vídeo?
-La ecuación diferencial es de la forma y'' - 6y' + 8y = 0.
¿Por qué se propone una solución de tipo exponencial para la ecuación diferencial?
-Se propone una solución de tipo exponencial porque las funciones exponenciales son aquellas que tienen como derivadas a ellas mismas, lo que es coherente con la estructura de la ecuación diferencial.
¿Cómo se calculan las derivadas de una función exponencial en el contexto del vídeo?
-La primera derivada de una función de la forma e^(rx) es r*e^(rx), y la segunda derivada es r^2*e^(rx).
¿Cómo se sustituye la solución propuesta en la ecuación diferencial para resolverla?
-Se sustituye la solución propuesta en la ecuación diferencial, calculando las derivadas correspondientes y simplificando para obtener una ecuación en términos de r.
¿Qué se factoriza en el proceso de resolución de la ecuación diferencial?
-Se factoriza la expresión r^2 - 6r + 8, que se obtiene al simplificar la ecuación diferencial tras sustituir la solución propuesta.
¿Cuáles son los valores posibles para r tras factorizar la expresión en el vídeo?
-Los valores posibles para r son 2 y 4, ya que se resuelven las ecuaciones r - 2 = 0 y r - 4 = 0.
¿Cómo se obtienen las soluciones de la ecuación diferencial a partir de los valores de r?
-Se sustituyen los valores de r en la solución propuesta e^(rx) para obtener las soluciones e^(2x) y e^(4x).
¿Qué es la solución general de la ecuación diferencial y cómo se obtiene?
-La solución general es una combinación lineal de las soluciones particulares, es decir, c1*e^(2x) + c2*e^(4x), donde c1 y c2 son constantes arbitrarias.
¿Qué es la ecuación característica y cómo se relaciona con la ecuación diferencial?
-La ecuación característica es una ecuación de segundo grado que se obtiene a partir de la ecuación diferencial al reemplazar y simplificar, y cuyas soluciones son los valores de r que determinan las soluciones de la ecuación diferencial.
¿Cómo se pueden obtener soluciones complejas en ecuaciones diferenciales de este tipo?
-Se pueden obtener soluciones complejas si los valores de r son complejos, lo que ocurre cuando la ecuación característica tiene discriminante negativo.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
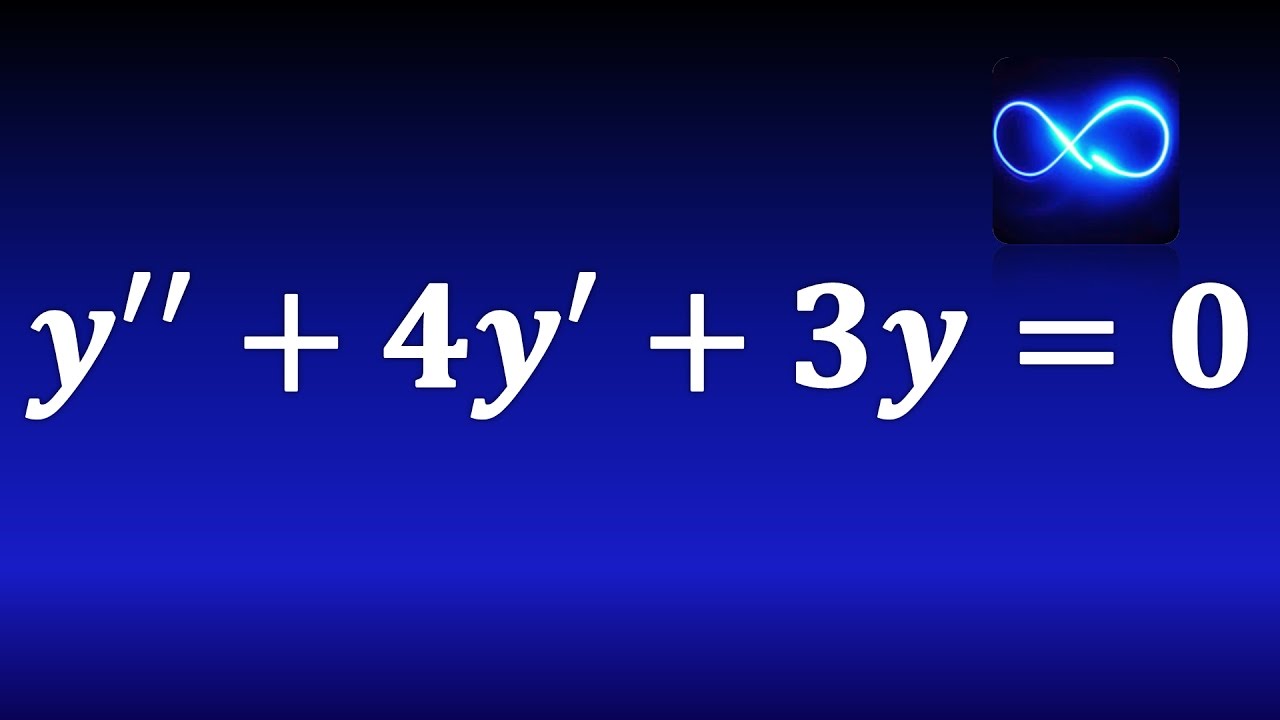
87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

96. Ecuación diferencial de coeficientes constantes, raíces repetidas. EJERCICIO RESUELTO.
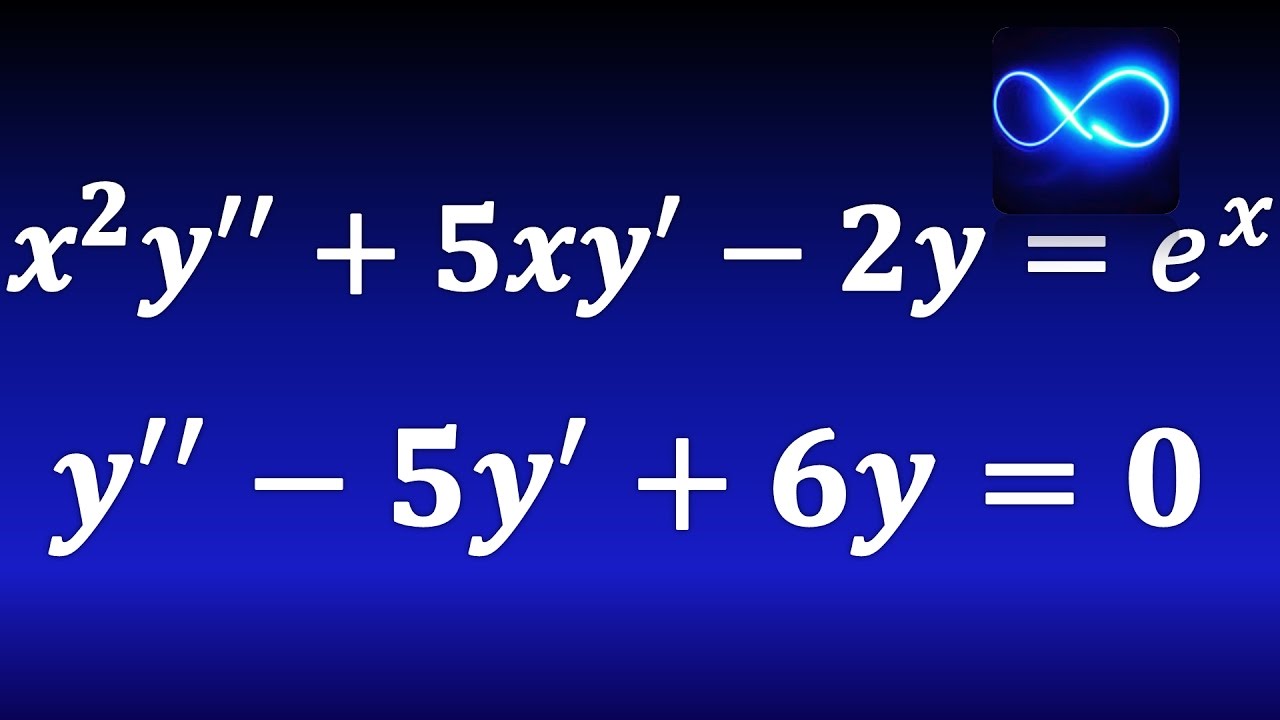
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

1. Ecuación diferencial de variables separables

01. Modelo simple de población, Ecuaciones Diferenciales

90. Ecuación diferencial de coeficientes constantes (Con una raíz igual a cero) EJERCICIO RESUELTO
5.0 / 5 (0 votes)
