03 01 Fisika Dasar 1- Pengenalan Vektor
Summary
TLDRThis educational video script delves into the concept of vectors, distinguishing between scalar and vector quantities. It explains that vectors possess both magnitude and direction, requiring special notation, often an arrow above the symbol. The script uses examples to illustrate how to determine the direction of a vector and introduces the idea of vector components along the x and y axes. It further explains how to calculate these components using trigonometric ratios and the Pythagorean theorem, providing a foundational understanding of vector analysis in two and three dimensions.
Takeaways
- 📚 The video script discusses the concept of vectors and scalars, distinguishing between those quantities that have both magnitude and direction (vectors) and those that have only magnitude (scalars).
- 📐 Vectors are quantities that require both magnitude and direction for complete specification, such as position or displacement.
- 🔢 Scalars are quantities that have magnitude but no direction, like mass or time, and do not require directional information.
- 🖊️ Vectors are denoted with a special notation, often using an arrow above the symbol (e.g., \( \vec{Q} \)) or boldface type to differentiate them from scalars.
- 🧭 The direction of a vector is represented by the angle it makes with a reference axis, such as the horizontal axis in a coordinate system.
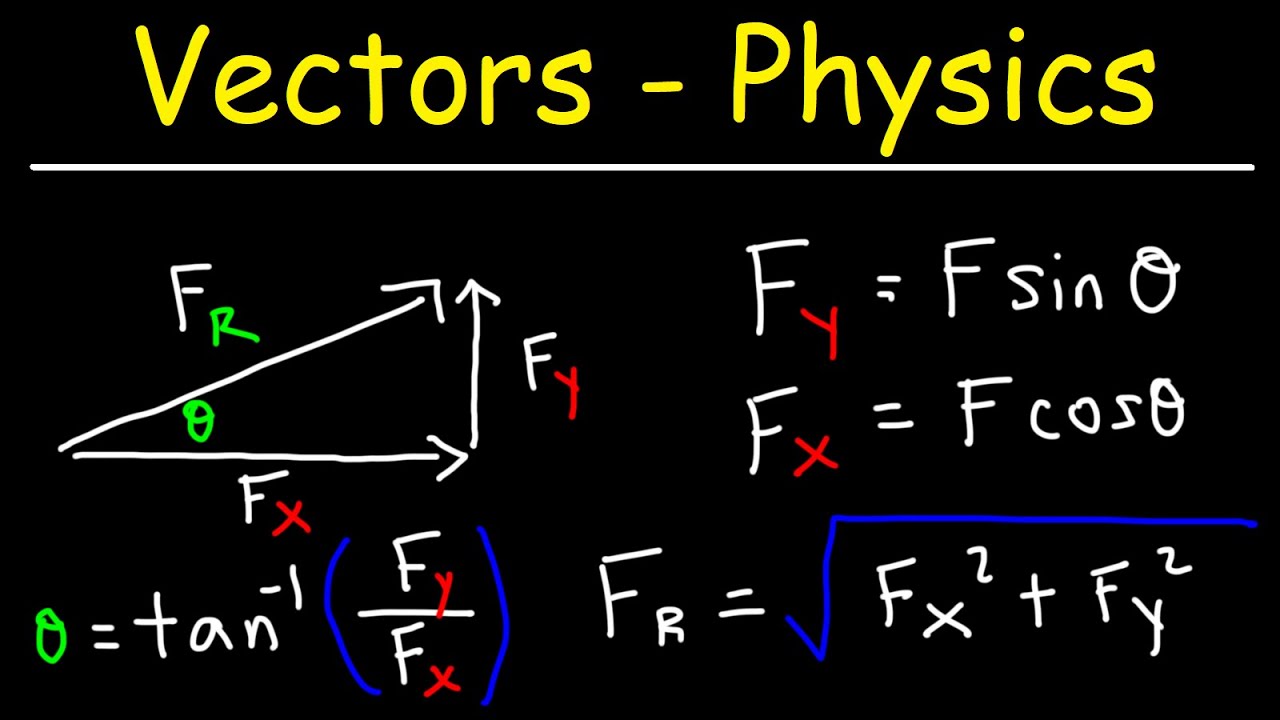
- 📏 To determine the components of a vector, one can use trigonometric ratios like sine, cosine, and tangent, which relate the vector's magnitude to its components along the coordinate axes.
- 🔄 The script explains how to break down a vector into its x and y components using the Pythagorean theorem, which states that the square of the vector's magnitude equals the sum of the squares of its components.
- 📈 The process of vector decomposition into components is crucial for performing vector operations such as addition, subtraction, and scalar multiplication.
- 📊 In three dimensions, a vector can be decomposed into components along the x, y, and z axes, and these components can be represented using unit vectors i, j, and k.
- 🔢 The magnitude of a vector in three dimensions can be calculated using the formula \( \sqrt{Q_x^2 + Q_y^2 + Q_z^2} \), where \( Q_x \), \( Q_y \), and \( Q_z \) are the components of the vector along the respective axes.
Q & A
What are the two types of quantities mentioned in the script?
-The two types of quantities mentioned are vector quantities, which have both magnitude and direction, and scalar quantities, which only have magnitude without direction.
What is the difference between a vector and a scalar?
-A vector is a quantity that has both magnitude and direction, while a scalar is a quantity that has magnitude but no direction.
How is a vector represented when written?
-A vector is represented with a notation that includes an arrow above the symbol, such as \( \vec{Q} \), or written in bold to indicate its direction.
Why is an arrow used as a symbol for vectors?
-An arrow is used as a symbol for vectors because it represents both the magnitude and the direction of the vector, which are essential characteristics of a vector quantity.
What is the significance of the angle theta (θ) in the context of vectors?
-The angle theta (θ) represents the direction of the vector relative to a reference axis, such as the horizontal axis in a coordinate system.
How can you determine if two vectors are the same based on the script?
-Two vectors are considered the same if they have the same length (magnitude) and the same direction.
What are the components of a vector in a two-dimensional space?
-The components of a vector in a two-dimensional space are its projections onto the x-axis and y-axis, often referred to as the x-component and y-component.
How can you express a vector in terms of its components using unit vectors?
-A vector can be expressed in terms of its components using unit vectors as \( \vec{Q} = Q_x \hat{i} + Q_y \hat{j} \), where \( \hat{i} \) and \( \hat{j} \) are the unit vectors in the direction of the x-axis and y-axis, respectively.
What is the relationship between the vector components and the vector's magnitude?
-The vector's magnitude can be calculated using the Pythagorean theorem, where the magnitude is the square root of the sum of the squares of its components (\( \sqrt{Q_x^2 + Q_y^2} \)).
How does the script explain the use of trigonometry in vector analysis?
-The script explains the use of trigonometry by relating the vector components to the sides of a right-angled triangle, where the sine, cosine, and tangent of an angle can be used to find the components based on the angle and the magnitude of the vector.
What is the significance of the Pythagorean theorem in determining the magnitude of a vector?
-The Pythagorean theorem is used to determine the magnitude of a vector by calculating the square root of the sum of the squares of its components, which is essential for understanding the vector's overall size in a two-dimensional or three-dimensional space.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Vectors - Basic Introduction - Physics

Besaran vektor dan besaran skalar (Fisika SMA/MA Sagufindo kls X smt 1 : Vektor)

GRANDEZAS FÍSICAS (ESCALARES E VETORIAIS) | Resumo de Física Enem. |Prof Marcus Rossetto

Fisika SMA - Vektor (1) - Pengenalan Vektor, Besaran Vektor dan Skalar, Melukis Vektor Satuan (I)

Vektor 1

Konsep Dasar Vektor (Vektor Bagian 1) Matematika Peminatan Kelas 10 - m4thlab
5.0 / 5 (0 votes)
