Vectors - Basic Introduction - Physics

Summary

This educational video script explores the concept of vectors, distinguishing them from scalars by their magnitude and direction. It clarifies that displacement, velocity, and acceleration are vectors, unlike mass, which is a scalar. The script delves into calculating vector components using trigonometry, specifically for a force vector at a 30-degree angle, and introduces unit vectors for expressing vector quantities in a coordinate system.

Takeaways

• 📚 Vectors are quantities with both magnitude and direction, unlike scalars which only have magnitude.
• 🌡️ Scalar quantities, such as temperature, have magnitude but no direction, making them unable to be associated with a direction.
• 📍 Force is a vector because it can be described with both magnitude and direction, such as 100 newtons at a 30-degree angle.
• 🚶 Distance is a scalar, but displacement is a vector, as it includes direction, like running '45 meters east'.
• 🏃 Velocity is a vector, combining speed (a scalar) with direction, telling you both how fast and in which direction something is moving.
• 📉 Acceleration is a vector that describes how quickly the velocity of an object is changing.
• 🧠 Understanding the difference between scalar and vector quantities is crucial for solving physics problems involving motion.
• 📐 Trigonometry plays a key role in breaking down vectors into their components using sine, cosine, and tangent functions.
• 📈 The x and y components of a vector can be found using the formulas: \( F_x = F \cdot \cos(\theta) \) and \( F_y = F \cdot \sin(\theta) \).
• 📐 The angle of a vector can be calculated using the arctan function: \( \theta = \arctan(\frac{F_y}{F_x}) \).
• 📊 The magnitude of a vector can be found using the Pythagorean theorem: \( F = \sqrt{F_x^2 + F_y^2} \).
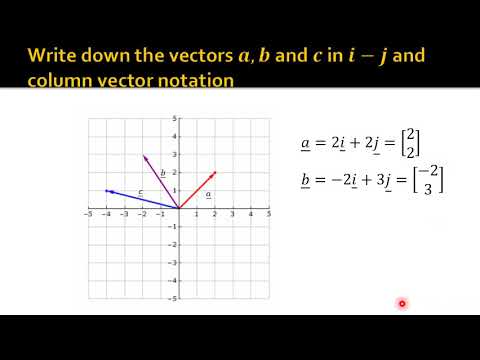
• 📝 Expressing vectors in component form using standard unit vectors (i, j, k) is a common method in vector notation.

Q & A

What is the main difference between a scalar and a vector quantity?

A scalar quantity has only magnitude and no direction, such as temperature, while a vector quantity has both magnitude and direction, like force.

Why is mass considered a scalar quantity?

Mass is considered a scalar quantity because it only has magnitude and no direction. For example, an object can have a mass of 10 kilograms, but it doesn't make sense to say it has a mass of 10 kilograms north.

How do you differentiate between displacement and distance?

Distance is a scalar quantity that measures how far an object has moved without considering direction, while displacement is a vector quantity that includes both the distance and the direction of movement.

How can velocity be distinguished from speed?

Speed is a scalar quantity that measures how fast an object is moving, while velocity is a vector quantity that includes both speed and direction.

What does acceleration measure, and why is it a vector?

Acceleration measures the rate at which velocity changes over time, and it is a vector because it has both magnitude and direction.

How do you calculate the x and y components of a force vector given its magnitude and angle?

The x component (F_x) is calculated using F_x = F * cos(θ), and the y component (F_y) is calculated using F_y = F * sin(θ), where F is the magnitude of the force and θ is the angle above the x-axis.

What is the significance of the SOHCAHTOA mnemonic in trigonometry?

SOHCAHTOA is a mnemonic that helps remember the definitions of sine, cosine, and tangent in relation to a right triangle: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, and Tangent = Opposite/Adjacent.

How is the magnitude of a vector determined from its x and y components?

The magnitude of a vector is determined using the Pythagorean theorem: Magnitude = √(F_x^2 + F_y^2), where F_x and F_y are the x and y components of the vector.

What is a unit vector, and how is it represented in the context of force vectors?

A unit vector is a vector with a magnitude of one. In the context of force vectors, unit vectors are represented by i, j, and k along the x, y, and z axes, respectively.

How can a force vector be expressed using standard unit vectors?

A force vector can be expressed using standard unit vectors by combining the x and y components with their respective unit vectors. For example, a force vector with components F_x and F_y can be written as F = F_x * i + F_y * j.