DIT FFT | 8 point | Butterfly diagram

Summary

This video explains the process of converting a time-domain signal into a frequency-domain signal using the DFT (Discrete Fourier Transform) and FFT (Fast Fourier Transform) algorithms. It starts by detailing how to write a sequence of elements, convert it into normal form, and then perform bit reversal. The script goes step-by-step through the process of constructing DFT stages, including two-point, four-point, and eight-point DFTs, with a focus on multiplying by twiddle factors at each stage. The end goal is to transform a time-domain signal into a frequency-domain representation, showcasing the detailed process of DFT and FFT algorithms.

Takeaways

• 😀 The Discrete Fourier Transform (DFT) and Fast Fourier Transform (FFT) are used to convert a time-domain signal into a frequency-domain signal.
• 😀 The time-domain signal is first written as a sequence, with elements labeled as x(0), x(1), ..., up to x(7).
• 😀 The process begins by writing the normal form of the sequence, which is then converted into bit reversal form to facilitate the FFT computation.
• 😀 In bit reversal, the binary representation of each sequence element is reversed to create a reordered sequence, which is necessary for FFT calculations.
• 😀 The bit reversal process involves reversing the order of binary digits in the indices and reordering the corresponding values.
• 😀 The algorithm uses stages: the first stage is 2-point DFT, the second stage is 4-point DFT, and the third stage is the final 8-point DFT.
• 😀 The DFTs in each stage are drawn using a 'butterfly' diagram, where each stage involves connecting lines to represent the combination of elements in the DFT calculation.
• 😀 In FFT, the twiddle factor (w) is multiplied at each stage, beginning with w^0 (which is 1) for the first stage and progressing to higher powers in subsequent stages.
• 😀 The values of the DFT are calculated at each stage by adding and subtracting values from the previous stage's results, adjusting them by the corresponding twiddle factor.
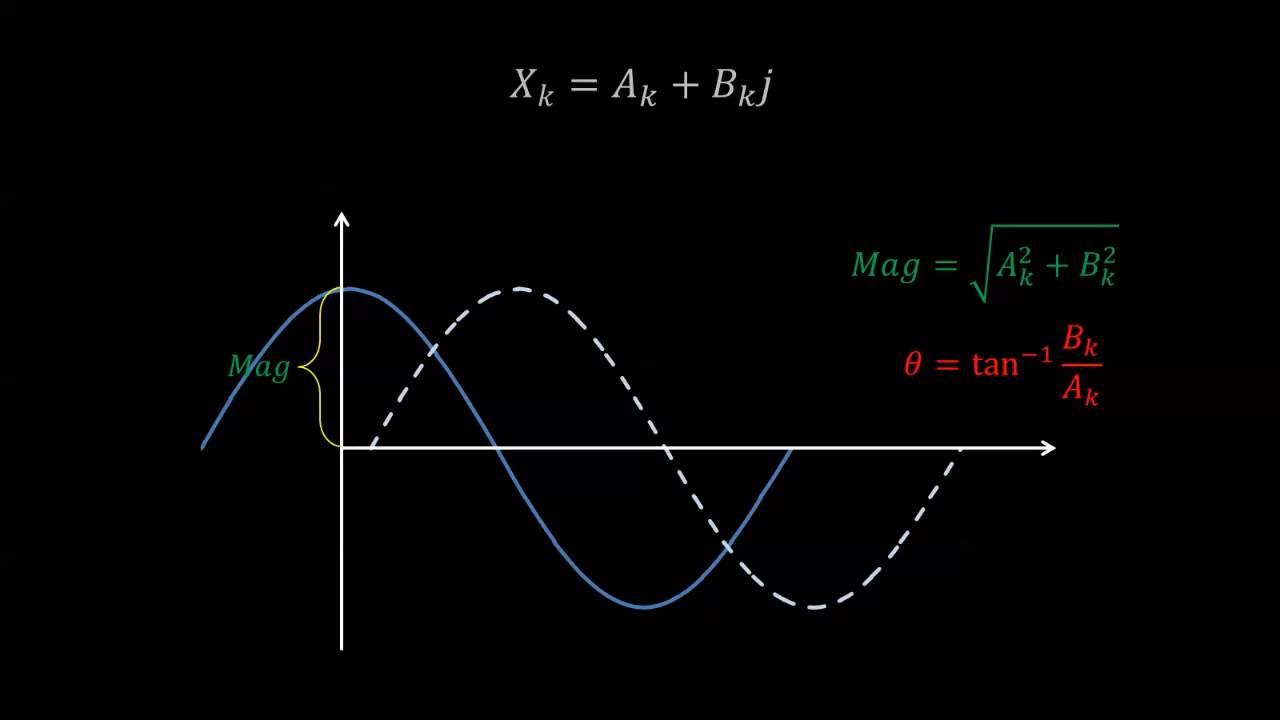
• 😀 The final output of the FFT is the frequency-domain signal, which contains complex values that represent the amplitude and phase of different frequency components.

Q & A

What is the main purpose of using the DFT/FFT algorithm in this context?

The main purpose of using the DFT/FFT algorithm in this context is to convert a time-domain signal into a frequency-domain signal. This process allows for analysis of the frequency components present in the signal.

What is the first step in converting the time-domain signal to the frequency domain?

The first step is to write the sequence of the time-domain signal. The elements of the sequence are labeled as x(0), x(1), x(2), and so on, up to x(7), representing eight elements.

How is the normal form of the sequence represented in this process?

The normal form of the sequence is simply the original sequence of numbers written in the same order. In this case, the sequence is written as x(0), x(1), x(2), and so on, before any transformations like bit reversal are applied.

What is bit reversal and why is it necessary in the FFT process?

Bit reversal is a transformation that reverses the bit positions of the indices of the sequence. This is necessary for the efficient implementation of the FFT algorithm, particularly in the decimation-in-time (DIT) approach.

What are the stages involved in the FFT algorithm described in the script?

The FFT algorithm in the script involves three stages: the first stage is a two-point DFT, the second stage is a four-point DFT, and the third stage is an eight-point DFT.

How is the two-point DFT represented in the diagram?

In the diagram, the two-point DFT is represented by two lines, with a 'cos mark' placed between the lines. The process starts by connecting the lines in specific patterns, following the decimation-in-time approach.

What is the role of the 'twiddle factor' in the FFT process?

The twiddle factor is used to multiply the values in the DFT algorithm. It represents the complex roots of unity and is crucial for calculating the frequency-domain values in the FFT algorithm. In the script, the twiddle factor is applied before and after the cos marks in each stage of the FFT.

How are the values calculated for each stage of the DFT?

In each stage of the DFT, values are calculated by summing the results of specific line connections and applying the twiddle factors. For example, the value at a specific point is determined by adding the results from two lines, with the second line often being multiplied by a twiddle factor before adding.

What is the final output of the DFT/FFT process?

The final output of the DFT/FFT process is the frequency-domain signal, represented as X(k). This sequence contains the frequency components of the original time-domain signal, and its values include both real and imaginary parts.

Why is the DFT/FFT algorithm important for signal analysis?

The DFT/FFT algorithm is important for signal analysis because it allows us to understand the frequency content of a signal, which is crucial in fields like communications, audio processing, and spectral analysis. It enables the identification of dominant frequencies and their amplitudes, which are often hidden in the time domain.