Relation between Laplace transform, Fourier transform, z-transform, DTFT, DFT and FFT

Summary

This video provides an overview of key transforms used in electrical engineering, including the Laplace transform, Fourier transform, Z transform, Discrete Time Fourier Transform (DTFT), and Discrete Fourier Transform (DFT). The video explores how these transforms are interconnected, with each one being a special case of another. It delves into the relationships between continuous and discrete transforms, explaining how the Fourier transform is derived from the Laplace transform, how the Z transform relates to the Laplace transform of discretized signals, and how the DFT is a sampled version of the DTFT. Additionally, the video touches on the Fast Fourier Transform (FFT) as an efficient algorithm to compute the DFT.

Takeaways

• 😀 The Laplace Transform converts a time-domain function into a complex function in the S-plane, where the variable 's' is complex (real + imaginary components).
• 😀 The Fourier Transform is a special case of the Laplace Transform, obtained by restricting the Laplace variable to the imaginary axis (s = jω).
• 😀 The Z Transform is the Laplace Transform of a discretized signal, transforming continuous-time signals into the Z-domain after sampling.
• 😀 The Discrete Time Fourier Transform (DTFT) is a special case of the Z Transform, where the Z variable lies on the unit circle in the Z-domain.
• 😀 The Discrete Fourier Transform (DFT) is a sampled version of the DTFT, representing a finite-length sequence in the frequency domain.
• 😀 The DFT is computed for finite-length sequences, making it implementable on digital hardware, whereas infinite-length sequences can't be processed directly.
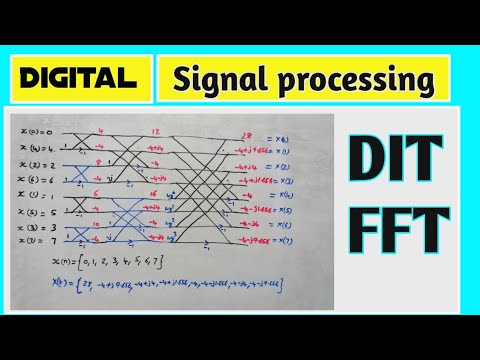
• 😀 The Fast Fourier Transform (FFT) is not a new transform but an efficient algorithm to compute the DFT, reducing computational complexity.
• 😀 The relationship between the Laplace and Fourier Transforms shows that forcing the Laplace variable to be purely imaginary gives the Fourier Transform.
• 😀 The Z Transform can be viewed as the Laplace Transform of a discretized signal, and the Z Transform evaluated on the unit circle gives the DTFT.
• 😀 The DTFT, when sampled, gives the DFT, and the DFT points correspond to the number of samples in the original discrete sequence.
• 😀 Understanding the relationships between these transforms helps simplify and solve various engineering problems, especially in electrical signal processing.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.