DSP#44 problem on 8 point DFT using DIT FFT in digital signal processing || EC Academy

Summary

In this video, the process of performing a Decimation in Time (DIT) Fast Fourier Transform (FFT) on a sequence of eight samples is explained. The speaker guides viewers through the FFT stages, including the butterfly diagram and bit reversal method for reordering the sequence. Each step of the calculation is thoroughly demonstrated, from finding intermediate results to computing the final Discrete Fourier Transform (DFT) values, including complex numbers. The video aims to provide a clear understanding of how to apply DIT FFT and obtain the frequency domain signal for a given sequence.

Takeaways

• 😀 The lecture explains how to compute the Discrete Fourier Transform (DFT) using the Decimation in Time (DIT) Fast Fourier Transform (FFT) method.
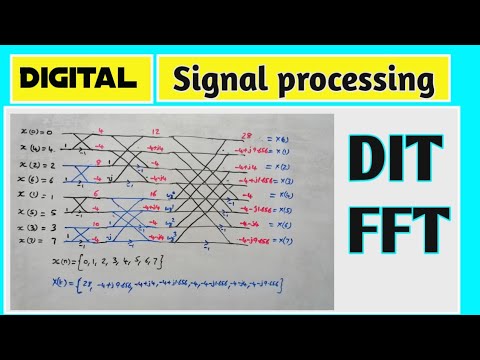
• 😀 The given sequence, x(n), consists of 8 samples, and the goal is to find x(k) using DIT FFT.
• 😀 The DIT FFT method involves drawing a butterfly diagram or signal flow diagram to represent the computation process.
• 😀 The input sequence x(n) is reordered using bit reversal or direct indexing as: x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7).
• 😀 The butterfly diagram for N=8 contains multiple stages, with each stage involving computations with different powers of the primitive root of unity (w).
• 😀 At the first stage, the butterfly calculations involve simple additions and subtractions of the inputs, using W8^0, W8^2, and so on.
• 😀 Intermediate results from each stage are carried forward to the next stage, where further calculations refine the results.
• 😀 The output values at each stage are calculated step-by-step by combining input values, multiplying them by appropriate powers of W, and summing or subtracting them.
• 😀 The final output values for x(k) are computed after applying the transformations at all stages. The results for x(k) are complex numbers.
• 😀 The lecture concludes by summarizing the final DFT values for the given sequence, showing the real and imaginary parts of x(k) for each k.

Q & A

What is the main objective of this lecture?

The main objective of the lecture is to understand how to find x(k) using the Decimation in Time Fast Fourier Transform (DIT FFT) method for a given sequence x(n).

What is the significance of drawing the butterfly diagram in DIT FFT?

The butterfly diagram is crucial as it visually represents the signal flow for the FFT process, showing how the input sequence is transformed through multiple stages to reach the final frequency-domain output.

Why is the process called 'Decimation in Time'?

It is called Decimation in Time because the time-domain signal is progressively decimated (divided or broken down) in stages, which is a key characteristic of the FFT process.

What is the size of the input sequence x(n) in this problem?

The size of the input sequence x(n) is 8, meaning there are 8 samples in the sequence.

What role does bit reversal play in the process?

Bit reversal is used to reorder the input sequence before applying the FFT algorithm. It helps in arranging the inputs in the correct order based on their binary representation.

What is the purpose of using the values w8^0, w8^1, w8^2, and so on in the process?

These values, which are powers of the primitive root of unity, are used as twiddle factors in the FFT algorithm to manipulate the input sequence during each stage of the computation.

What does the term 'twiddle factor' refer to in FFT?

A twiddle factor refers to the complex exponential terms (w8^k) used in the FFT algorithm that modulate the input values at each stage of computation.

How is the output of the FFT calculation obtained?

The output is obtained by repeatedly applying the FFT formula, which involves adding or subtracting the twiddle factors multiplied by the inputs, and then performing the calculation step by step through the stages.

What is the result of applying the DIT FFT process to the given input sequence x(n)?

The result of applying the DIT FFT process to the input sequence is the frequency-domain representation x(k), which includes complex values such as 255, 48.63 + j166.05, -51 + j102, and others.

Why is it important to use complex numbers during the FFT process?

Complex numbers are essential in the FFT process because the Fourier transform of a real-valued signal results in complex frequency-domain values, representing both amplitude and phase information.