Distribución de Poisson | Ejercicios resueltos | Intro
Summary
TLDREn este video, Jorge explica de manera detallada la distribución de Poisson, una distribución de probabilidad discreta fundamental en estadística. A través de ejemplos prácticos, como el número de pacientes que llegan a su veterinaria, Jorge ilustra cómo aplicar la fórmula de Poisson para calcular probabilidades en eventos como la llegada de tres o cinco pacientes en un día. Además, enfatiza la importancia de ciertos supuestos para aplicar correctamente esta distribución, como la independencia de los eventos y la constancia en la tasa de ocurrencia. Al final, resuelve ejercicios prácticos y plantea preguntas adicionales para involucrar a la audiencia.
Takeaways
- 😀 La distribución de Poisson es una distribución de probabilidad discreta importante en estadística que modela la cantidad de veces que ocurre un evento en un intervalo definido.
- 😀 Esta distribución fue propuesta por primera vez por Siméon-Denis Poisson en 1837 y ha tenido diversas aplicaciones, especialmente con la aparición de las computadoras.
- 😀 La variable aleatoria en la distribución de Poisson representa el número de veces que ocurre un evento en un intervalo de tiempo o espacio determinado.
- 😀 Los supuestos clave de la distribución de Poisson incluyen: la probabilidad de ocurrencia es constante, los eventos son independientes y dos eventos no pueden ocurrir exactamente al mismo tiempo.
- 😀 El intervalo para aplicar la distribución de Poisson puede ser de tiempo, distancia, área, volumen, entre otros.
- 😀 Un ejemplo práctico de Poisson en la vida real es la llegada de pacientes a una veterinaria, donde el número de pacientes por día sigue una distribución de Poisson.
- 😀 Para aplicar la fórmula de Poisson, se necesitan dos parámetros: la media o valor esperado del evento y el número de ocurrencias que se desea calcular.
- 😀 La fórmula de la distribución de Poisson se expresa como P(X=x) = (λ^x * e^(-λ)) / x!, donde λ es el valor esperado, x es el número de ocurrencias y e es la base de los logaritmos naturales.
- 😀 La probabilidad de que ocurra un número específico de eventos en un intervalo se calcula usando esta fórmula, y la probabilidad resultante puede expresarse en términos decimales o como porcentaje.
- 😀 En un ejemplo concreto, si una veterinaria recibe en promedio 4 pacientes al día, la probabilidad de recibir exactamente 3 pacientes en un día puede calcularse usando la fórmula de Poisson, resultando en un 19.54%.
- 😀 La distribución de Poisson es útil para modelar fenómenos donde los eventos ocurren de manera aleatoria pero siguen una tasa constante, como la llegada de autos a una gasolinera o la cantidad de bacterias en un litro de agua.
Q & A
¿Qué es la distribución de Poisson y por qué es importante en estadística?
-La distribución de Poisson es una distribución de probabilidad discreta que modela la cantidad de eventos que ocurren en un intervalo de tiempo o espacio determinado, bajo ciertas condiciones. Es importante en estadística porque se usa en muchas aplicaciones reales, como en la llegada de pacientes a una clínica o autos a una gasolinera.
¿Cuáles son los supuestos que deben cumplirse para que se aplique la distribución de Poisson?
-Los supuestos incluyen: 1) La probabilidad de ocurrencia es la misma para intervalos de igual longitud. 2) Los eventos son independientes entre sí. 3) Los eventos no pueden ocurrir exactamente al mismo tiempo.
¿Qué significa que las ocurrencias sean independientes en la distribución de Poisson?
-Significa que la ocurrencia de un evento no afecta la probabilidad de que ocurra otro evento. Por ejemplo, si un paciente llega a la clínica, su llegada no cambia la probabilidad de que otro paciente llegue.
¿Qué debe hacerse si los supuestos de la distribución de Poisson no se cumplen?
-Si los supuestos no se cumplen, ya no estaríamos frente a una distribución de Poisson. En esos casos, se debería buscar otro modelo estadístico que se ajuste mejor a los datos.
¿Cómo se interpreta el parámetro lambda (λ) en la distribución de Poisson?
-Lambda (λ) representa la tasa promedio de ocurrencias de un evento en un intervalo definido. En el ejemplo de la veterinaria, λ sería el número promedio de pacientes que llegan por día.
¿Qué fórmula se utiliza para calcular la probabilidad en la distribución de Poisson?
-La fórmula es: P(X = x) = (λ^x * e^(-λ)) / x!, donde λ es el valor esperado (media), x es el número de eventos deseado, e es la constante de Euler (aproximadamente 2.71828), y x! es el factorial de x.
En el contexto de la veterinaria de Jorge, ¿cómo se define la variable aleatoria X?
-En este contexto, la variable aleatoria X representa el número de pacientes que llegan a la veterinaria de Jorge en un día, que sigue una distribución de Poisson con un valor promedio de 4 pacientes al día.
¿Cómo se calcula la probabilidad de que lleguen tres pacientes a la veterinaria en un día?
-Se usa la fórmula de Poisson: P(X = 3) = (4^3 * e^(-4)) / 3! = 0.1954, lo que equivale a una probabilidad del 19.54%.
¿Qué sucede si se cambia el valor de λ (tasa promedio) en la distribución de Poisson?
-Si λ cambia, se modifica la tasa promedio de ocurrencias, lo que afectará la probabilidad de que ocurran diferentes cantidades de eventos. Un λ mayor indicaría más eventos por intervalo, y un λ menor indicaría menos eventos.
¿Cómo se calcula el factorial de un número y por qué es importante en la fórmula de Poisson?
-El factorial de un número x se calcula multiplicando todos los enteros positivos desde 1 hasta x. Es importante en la fórmula de Poisson porque ajusta la probabilidad de eventos basándose en cuántos eventos específicos se desean en el intervalo definido.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Función de probabilidad de variable aleatoria discreta | Ejercicio 1
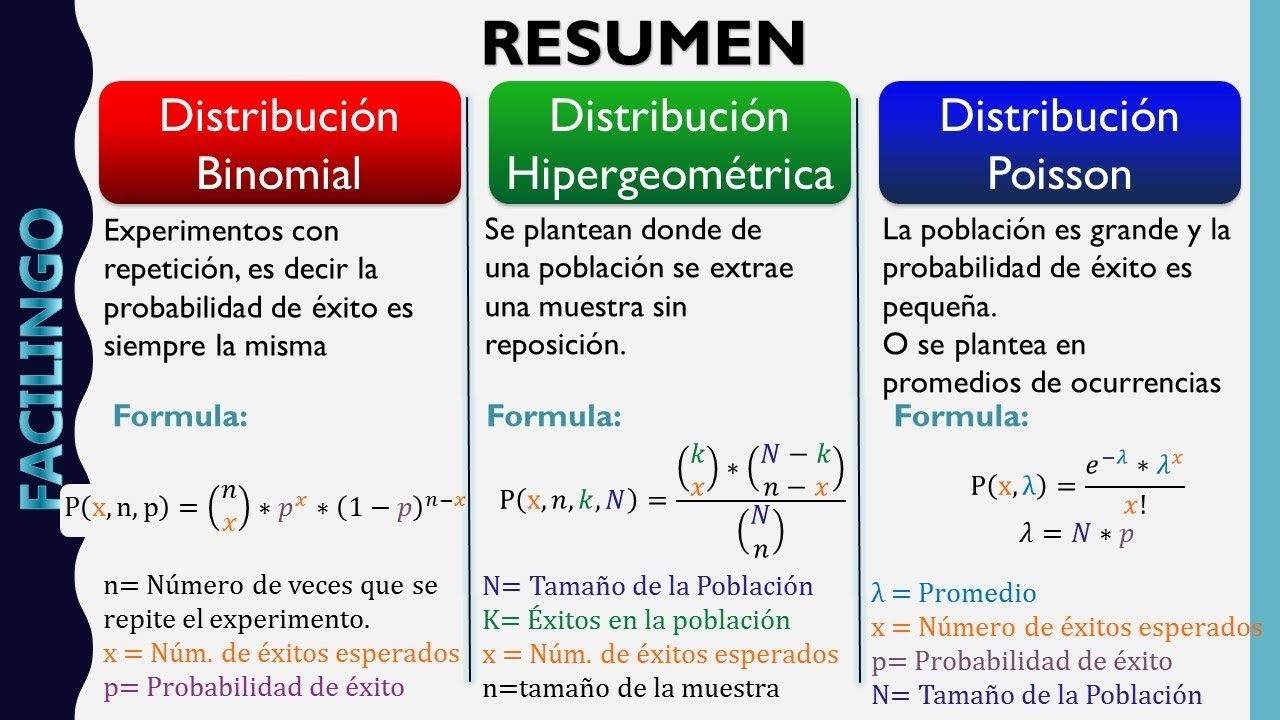
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

Distribución de Poisson | Teoría y ejercicio resuelto

¿Cuál es la probabilidad aseguradora pague 4 indemnizaciones en 1 año? Poisson en Excel

Ejemplo Distribución de Poisson (Probabilidad, Esperanza Matemática y Varianza)

DISTRIBUCIÓN t DE STUDENT | | UPV
5.0 / 5 (0 votes)
