Distribución de Poisson | Teoría y ejercicio resuelto
Summary
TLDREste vídeo educativo introduce la distribución de probabilidad de Poisson, una herramienta estadística para modelar eventos que ocurren con cierta frecuencia en intervalos de tiempo o espacio. El presentador explica detalladamente cómo calcular la probabilidad de que un evento ocurra un número específico de veces en un intervalo dado, utilizando el ejemplo de nacimientos de bebés varones en un hospital. Se resuelven ejercicios prácticos para ilustrar el concepto, y se enfatiza la importancia de que los eventos sean independientes para aplicar esta distribución. El vídeo termina con una invitación a los espectadores a suscribirse y participar en futuras lecciones sobre la media y varianza de la distribución de Poisson.
Takeaways
- 😀 La distribución de probabilidad de Poisson es utilizada para modelar la probabilidad de que un suceso ocurra un número de veces específico en un intervalo de tiempo, longitud o área.
- 📚 La variable aleatoria discreta en la distribución de Poisson representa el número de veces que un suceso ocurre, y es fundamental entender esta definición para resolver problemas relacionados.
- ✅ La fórmula de Poisson es e^{-λ} (λ^k) / k!, donde λ es el número promedio de veces que ocurre el suceso en el intervalo y k es el número de veces que se repite el suceso.
- 👶 En el ejemplo del vídeo, se calcula la probabilidad de que nazcan tres bebés varones en una semana en un hospital, donde el número promedio de nacimientos de varones es de siete por semana.
- 🔢 Se explicó cómo calcular la probabilidad de que ocurran menos de tres nacimientos de varones en una semana, sumando las probabilidades de 0, 1 y 2 nacimientos varones.
- 📉 La probabilidad de que ocurra un suceso menos veces que el promedio (en este caso, menos de tres varones) es menor que la probabilidad de que ocurra cerca del promedio o más veces.
- 📚 Se mencionan las propiedades necesarias para que una variable aleatoria sea de Poisson: los sucesos deben ser aleatorios y los eventos dentro del intervalo deben ser independientes.
- 🚫 Un ejemplo de eventos no independientes es la propagación de una enfermedad contagiosa, donde la infección de un individuo puede influir en la probabilidad de que otros se infecten.
- 📅 Se enfatiza que la distribución de Poisson se aplica comúnmente a intervalos de tiempo, pero también puede ser utilizada para intervalos de longitud, área o volumen.
- 🔑 La independencia de los eventos es crucial para la aplicación correcta de la distribución de Poisson; sin ella, no se puede aplicar la distribución.
Q & A
¿Qué es la distribución de probabilidad de Poisson?
-La distribución de probabilidad de Poisson es una distribución de una variable aleatoria discreta que nos proporciona la probabilidad de que ocurra un determinado suceso un número de veces en un intervalo determinado, como por ejemplo, un intervalo de tiempo, longitud o área.
¿Cuál es la importancia de entender la variable aleatoria discreta en el contexto de la distribución de Poisson?
-La variable aleatoria discreta es importante para entender la distribución de Poisson porque nos permite calcular la probabilidad de que un suceso ocurra un número específico de veces en un intervalo determinado.
¿Cómo se calcula la probabilidad en la distribución de Poisson?
-La probabilidad en la distribución de Poisson se calcula usando la fórmula: (e^(-λ) * (λ^k)) / k!, donde λ es el número promedio de veces que ocurre el suceso en el intervalo y k es el número de veces que se repite el suceso.
¿En qué tipo de intervalos se suele aplicar la distribución de Poisson?
-La distribución de Poisson se suele aplicar en intervalos de tiempo, pero también se puede usar en intervalos de longitud, área e incluso volumen.
¿Cuál es el ejemplo práctico que se utiliza en el guion para explicar la distribución de Poisson?
-Se utiliza el ejemplo de un hospital donde se estudia la cantidad de nacimientos de bebés varones en una semana, sabiendo que en promedio nacen siete varones por semana.
¿Cómo se calcula la probabilidad de que nazcan tres varones en una semana según la distribución de Poisson?
-Se aplica la fórmula de la distribución de Poisson con λ = 7 (la media de nacimientos de varones por semana) y k = 3, lo que resulta en una probabilidad del 5.2%.
¿Qué significa calcular la probabilidad de que nazcan menos de tres varones en una semana en el contexto de la distribución de Poisson?
-Esto implica calcular la probabilidad de que ocurran cero, uno o dos nacimientos de varones en una semana, sumando las probabilidades de estos eventos individuales.
¿Cuál es la probabilidad de que nazcan menos de tres varones en una semana según el ejemplo del hospital?
-La probabilidad de que nazcan menos de tres varones en una semana es del 29%, sumando las probabilidades de cero, uno y dos nacimientos de varones.
¿Qué condiciones deben cumplirse para que un suceso pueda ser estudiado con la distribución de Poisson?
-Los sucesos deben ser aleatorios y los eventos dentro del intervalo de estudio deben ser independientes, es decir, el ocurrir de un evento no debe afectar el ocurrir de otro.
¿Por qué no se puede aplicar la distribución de Poisson en situaciones donde los eventos no son independientes?
-En situaciones donde los eventos no son independientes, como en el contagio de una enfermedad, el suceso de un alumno enfermarse puede influir en que otros alumnos enfermen, por lo que no se cumple la condición de independencia necesaria para la distribución de Poisson.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
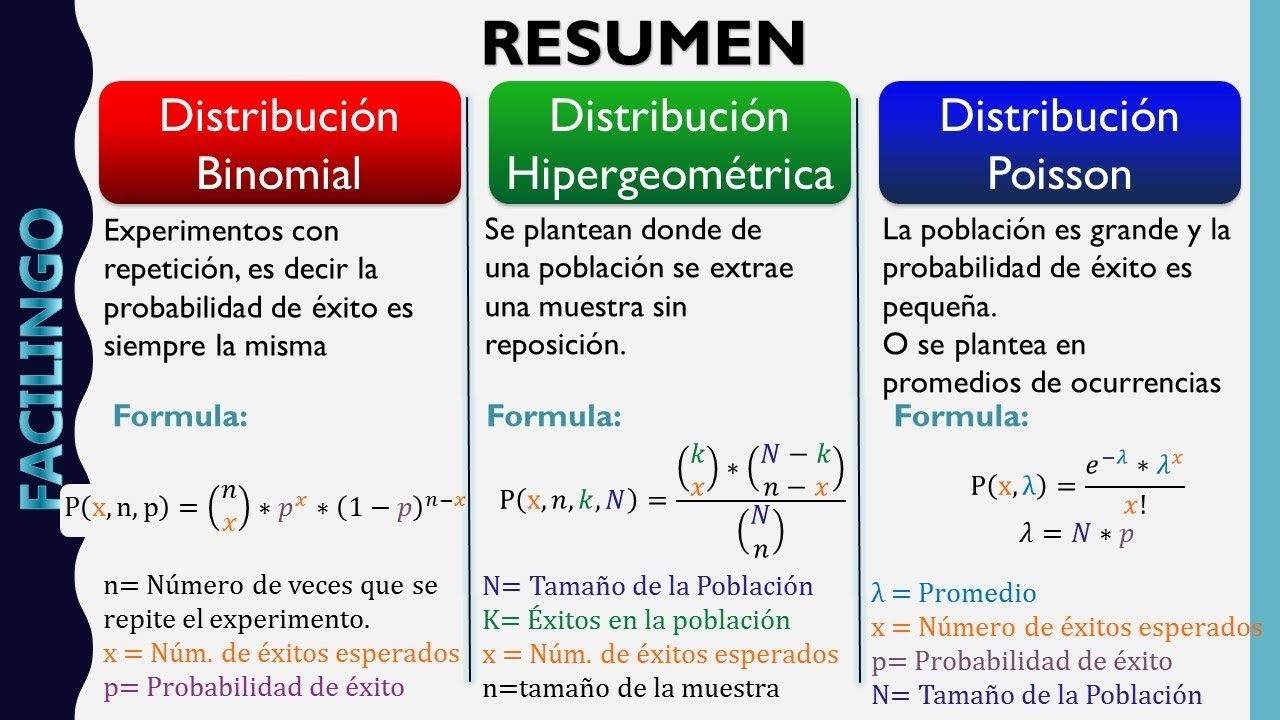
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

¿Cuál es la probabilidad aseguradora pague 4 indemnizaciones en 1 año? Poisson en Excel

Distribución de Poisson | Ejercicios resueltos | Intro

Progresión 3. Pensamiento matemático 1. DGETI 2023 MCCEMS

Probabilidad TEÓRICA Vs. Probabilidad FRECUENCIAL

Ejemplo Distribución de Poisson (Probabilidad, Esperanza Matemática y Varianza)
5.0 / 5 (0 votes)
