¿Cuál es la probabilidad aseguradora pague 4 indemnizaciones en 1 año? Poisson en Excel
Summary
TLDREn este video se explica cómo utilizar la distribución Poisson, una variante de la distribución binomial, para modelar eventos raros. A través de un ejemplo con una aseguradora que tiene 5000 clientes de 42 años, se calcula la probabilidad de que la compañía pague cuatro indemnizaciones por muertes en un año. Se detallan los pasos para calcular el valor esperado, aplicar la fórmula en Excel y visualizar los resultados con un histograma. Al final, se concluye que la probabilidad de pagar exactamente cuatro indemnizaciones es del 18%, proporcionando una visión clara sobre el uso de la distribución Poisson en situaciones prácticas.
Takeaways
- 😀 La distribución Poisson es útil para experimentos binomiales con muestras grandes y probabilidades pequeñas de éxito.
- 😀 La fórmula de la distribución Poisson se basa en el valor esperado (λ), que se obtiene multiplicando n (el tamaño de la muestra) por p (la probabilidad de éxito).
- 😀 Para calcular la probabilidad de un número específico de éxitos en una distribución Poisson, se utiliza la fórmula Poisson.PD en Excel.
- 😀 En un ejemplo de seguros, se calcula la probabilidad de que una aseguradora pague cuatro indemnizaciones por muertes en un año entre 5000 asegurados de 42 años.
- 😀 El valor esperado (λ) en el caso del ejemplo de seguros es 5, lo que indica que en promedio 5 de cada 5000 asegurados fallecerían en el año.
- 😀 La distribución Poisson es apropiada cuando la probabilidad de éxito es pequeña y el número de ensayos (n) es grande.
- 😀 La fórmula de Poisson se puede usar para determinar la probabilidad exacta de que ocurran entre 0 y 5000 muertes, aunque los valores disminuyen rápidamente después de cierto punto.
- 😀 En Excel, al aplicar la función POISSON.DIST, se puede calcular la probabilidad de un número específico de éxitos (muertes) o la probabilidad acumulada.
- 😀 La construcción de un histograma de los resultados ayuda a visualizar la distribución de las probabilidades de manera clara y efectiva.
- 😀 Es importante recordar que, aunque en teoría se podría calcular hasta 5000 valores, en la práctica solo los primeros valores significativos son relevantes para el análisis, ya que después de un punto la probabilidad es prácticamente cero.
Q & A
¿Qué es la distribución de Poisson y cómo se relaciona con la distribución binomial?
-La distribución de Poisson es similar a un experimento binomial, pero se aplica en situaciones donde la muestra es muy grande (n muy grande) y la probabilidad de éxito es pequeña. Esta distribución describe el número de eventos que ocurren en un intervalo de tiempo o espacio dado, bajo ciertas condiciones.
¿Cuáles son las condiciones para usar la distribución de Poisson en lugar de la distribución binomial?
-La distribución de Poisson se utiliza cuando el tamaño de la muestra (n) es muy grande o la probabilidad de éxito (p) es muy pequeña, o en ambos casos. Es adecuada para modelar eventos raros en grandes poblaciones.
En el ejemplo del video, ¿cuál es el valor de n y de p?
-En el ejemplo, n es 5000 (el número de asegurados) y p es 0.001 (la probabilidad de que un hombre de 42 años muera en un año).
¿Cómo se calcula el valor esperado (lambda) en la distribución de Poisson?
-El valor esperado (lambda) se calcula multiplicando n por p. En este caso, lambda = 5000 * 0.001 = 5, lo que indica que, en promedio, se espera que mueran 5 hombres de 42 años entre los 5000 asegurados en un año.
¿Cuál es la fórmula de la distribución de Poisson que se utiliza para calcular la probabilidad?
-La fórmula es: P(X = x) = (e^(-λ) * λ^x) / x!, donde e es la base del logaritmo natural, λ es el valor esperado (n * p), x es el número de éxitos deseados, y x! es el factorial de x.
¿Qué herramienta se utiliza en el video para calcular la distribución de Poisson y cómo se aplica?
-En el video se utiliza Excel, específicamente la función 'POISSON.DIST'. Esta función permite calcular la probabilidad de obtener un número determinado de eventos en una distribución de Poisson, dado un valor de lambda y el número de eventos (x).
¿Por qué se utiliza el número 15 como límite en la tabla de distribución de probabilidad en lugar de hasta 5000?
-El número 15 se usa como límite práctico porque, a partir de ese punto, las probabilidades de obtener más de 15 eventos son tan pequeñas que se acercan a cero. Incluir más valores no aportaría información significativa para el análisis.
¿Qué representa el gráfico de barras (histograma) en el video?
-El histograma muestra la distribución de probabilidades de la cantidad de muertes en el grupo de 5000 hombres. A medida que aumenta el número de eventos (muertes), la probabilidad de que ocurran esos eventos disminuye rápidamente, lo que se refleja en la forma del gráfico.
¿Qué significa la probabilidad de 0.18 mencionada al final del video?
-La probabilidad de 0.18 es la probabilidad de que la compañía de seguros tenga que pagar exactamente 4 indemnizaciones en un año, según la distribución de Poisson calculada para el caso específico de 5000 asegurados.
¿Cómo se calcula la probabilidad acumulada o bruta en la distribución de Poisson?
-La probabilidad bruta se calcula usando la función 'POISSON.DIST' con el argumento 'falso' para obtener la probabilidad exacta de un número de eventos específico. Si se desea la probabilidad acumulada, se utiliza 'verdadero', lo que devuelve la probabilidad de obtener un número de eventos igual o menor a un valor dado.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
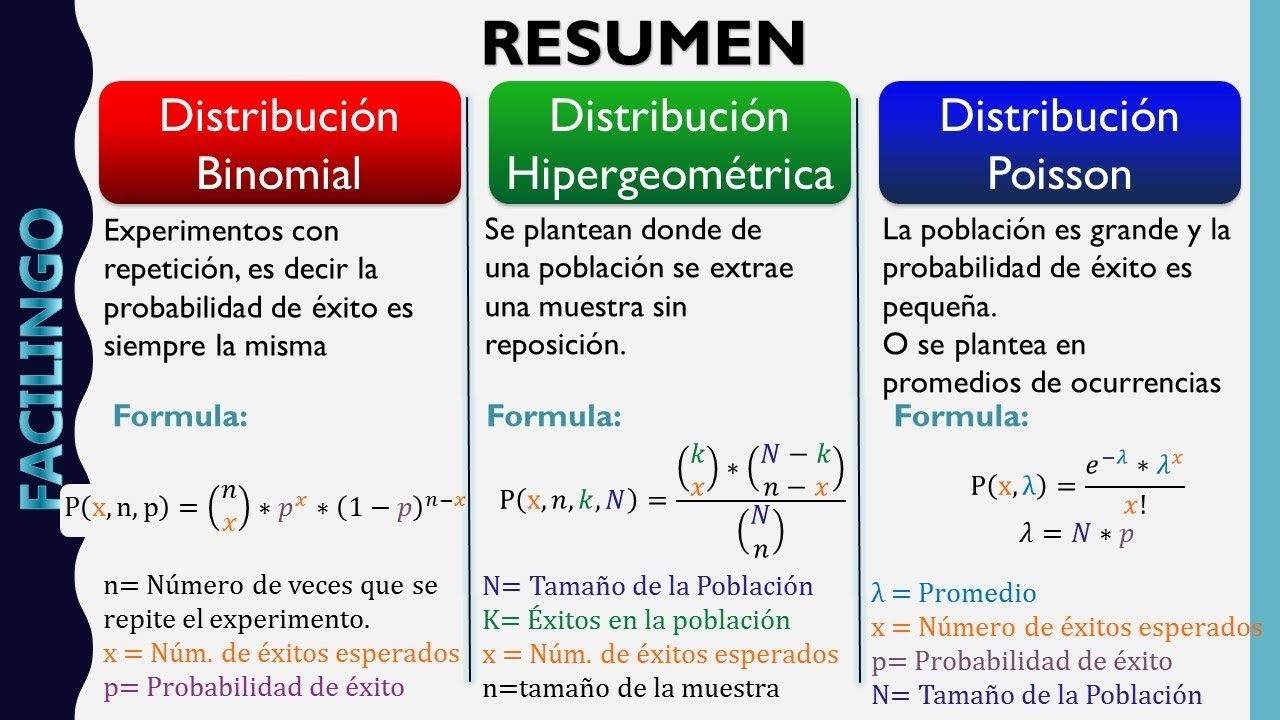
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

Distribución de Poisson | Teoría y ejercicio resuelto

Ejemplo Distribución de Poisson (Probabilidad, Esperanza Matemática y Varianza)

Distribución de Poisson | Ejercicios resueltos | Intro

Las distribuciones Bernoulli, binomial y normal

Distribución Hipergeométrica
5.0 / 5 (0 votes)
