Gerak Dua Dimensi "Fisika Dasar"
Summary
TLDRIn this lecture on two-dimensional motion, the professor explains how motion in two dimensions is more complex than one-dimensional motion, involving both x and y components. Key concepts like position vectors, displacement, and their calculations are discussed, with emphasis on vector components along the axes. The lecture covers how to compute displacement using the difference in position vectors, apply the Pythagorean theorem to find magnitudes, and determine the direction of displacement using trigonometry. Real-world examples, such as a particle moving from point P to Q, illustrate how these principles are applied in practice.
Takeaways
- 😀 Two-dimensional motion involves components along both the x and y axes, unlike one-dimensional motion which only considers one axis.
- 😀 In two-dimensional motion, position is represented as a vector with components along the x and y axes: r = x i + y j.
- 😀 Vectors have both magnitude and direction, distinguishing them from scalars which only have magnitude.
- 😀 The position vector gives the location of a point in two-dimensional space, expressed using unit vectors i (for x) and j (for y).
- 😀 Displacement is the change in position from one point to another and is calculated as the difference between the two position vectors: Δr = rQ - rP.
- 😀 The magnitude of displacement is found using the Pythagorean theorem: |Δr| = √(Δx² + Δy²).
- 😀 Direction of displacement is determined by calculating the angle θ using the formula: θ = tan⁻¹(Δy / Δx).
- 😀 Scalar quantities, like speed, only have magnitude, whereas vector quantities, like velocity, have both magnitude and direction.
- 😀 The example problem demonstrates how to calculate displacement, with points P(3, 2) and Q(11, 8), resulting in a displacement vector of 8i + 6j.
- 😀 The final displacement vector is 10 units in magnitude and has an angle of 36.87° relative to the positive x-axis.
- 😀 The lecture emphasizes the importance of breaking down motion into components and understanding how to use vectors to represent position and displacement.
Q & A
What is the difference between one-dimensional and two-dimensional motion?
-One-dimensional motion involves movement along a single axis (either x or y), whereas two-dimensional motion involves movement in both the x and y directions, making it more complex and requiring the consideration of both components separately.
How is the position of a particle in two-dimensional motion represented?
-The position of a particle in two-dimensional motion is represented as a vector in the form of r = x i + y j, where 'x' is the position along the x-axis and 'y' is the position along the y-axis. The 'i' and 'j' are unit vectors along the x and y directions, respectively.
What are the two types of quantities in physics discussed in the transcript?
-The two types of quantities discussed are vector quantities, which have both magnitude and direction (e.g., velocity), and scalar quantities, which only have magnitude (e.g., speed).
What is displacement in two-dimensional motion?
-Displacement in two-dimensional motion refers to the change in position of a particle, which is a vector quantity. It is calculated as the difference between the final position vector and the initial position vector (Δr = rQ - rP).
How can the displacement vector be calculated?
-The displacement vector is calculated by subtracting the initial position vector (rP) from the final position vector (rQ). Mathematically, Δr = rQ - rP.
What role does the Pythagorean theorem play in calculating displacement?
-The Pythagorean theorem is used to calculate the magnitude of the displacement vector when the components along the x and y axes are perpendicular to each other. The magnitude of the displacement is given by Δr = √(Δx² + Δy²).
What does the formula 'Delta R = Delta X i + Delta Y j' represent?
-The formula 'Delta R = Delta X i + Delta Y j' represents the displacement vector in two-dimensional motion, where ΔX is the change in position along the x-axis and ΔY is the change in position along the y-axis. 'i' and 'j' are unit vectors along the x and y directions.
How is the angle of the displacement vector calculated?
-The angle θ of the displacement vector relative to the positive x-axis is calculated using the tangent function: θ = tan⁻¹(Δy/Δx), where Δy and Δx are the changes in the y and x coordinates, respectively.
What is the significance of the unit vectors 'i' and 'j' in the context of displacement?
-'i' and 'j' are unit vectors used to indicate direction in the x and y components of displacement, respectively. They allow the displacement vector to be expressed in terms of its x and y components, making it easier to calculate and analyze.
What happens if the displacement vector forms a 90-degree angle?
-If the displacement vector forms a 90-degree angle, the Pythagorean theorem can be directly applied to find the magnitude of the displacement. In such cases, the components of the vector along the x and y axes are perpendicular, simplifying the calculation.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
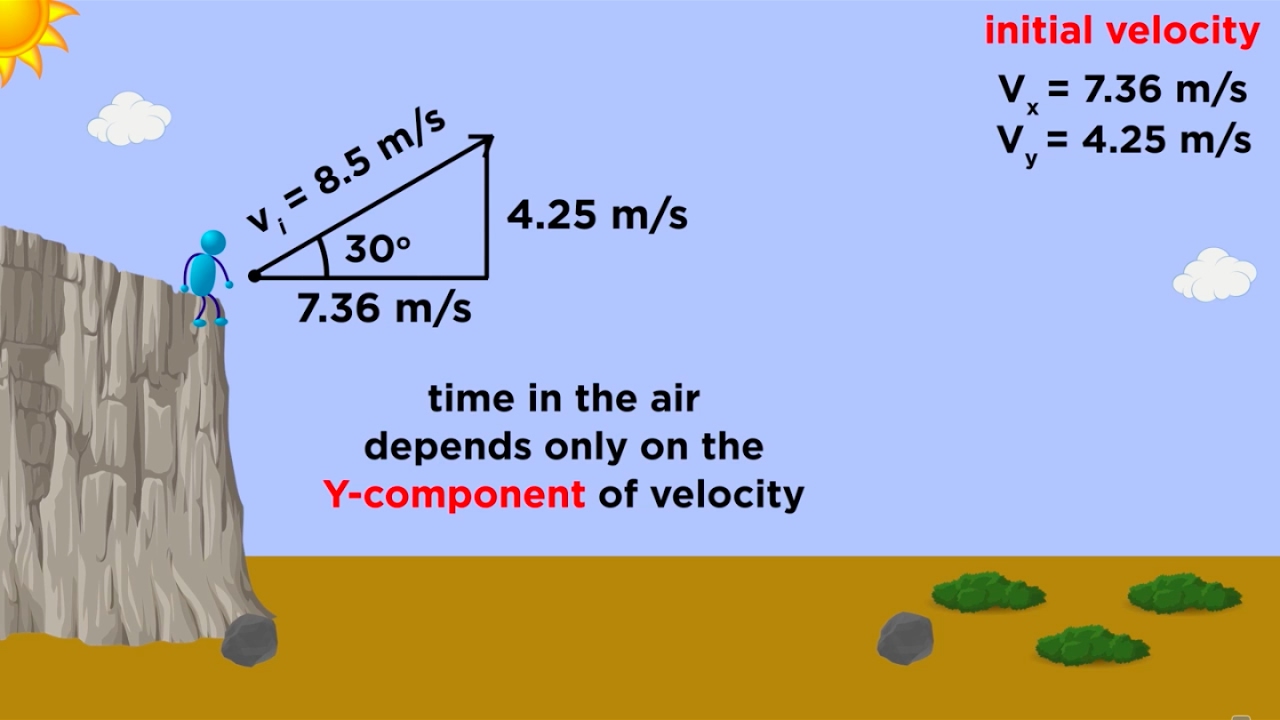
Kinematics Part 3: Projectile Motion

FISIKA KINEMATIKA KELAS XI JARAK PERPINDAHAN KELAJUAN KECEPATAN PART 1 KURIKULUM MERDEKA

Grade 11 Sc | Ch 7: Kinematics | 7.3. Position Vector (1)

Two Dimensional Motion (4 of 4) Horizontal Projection, Worked Example
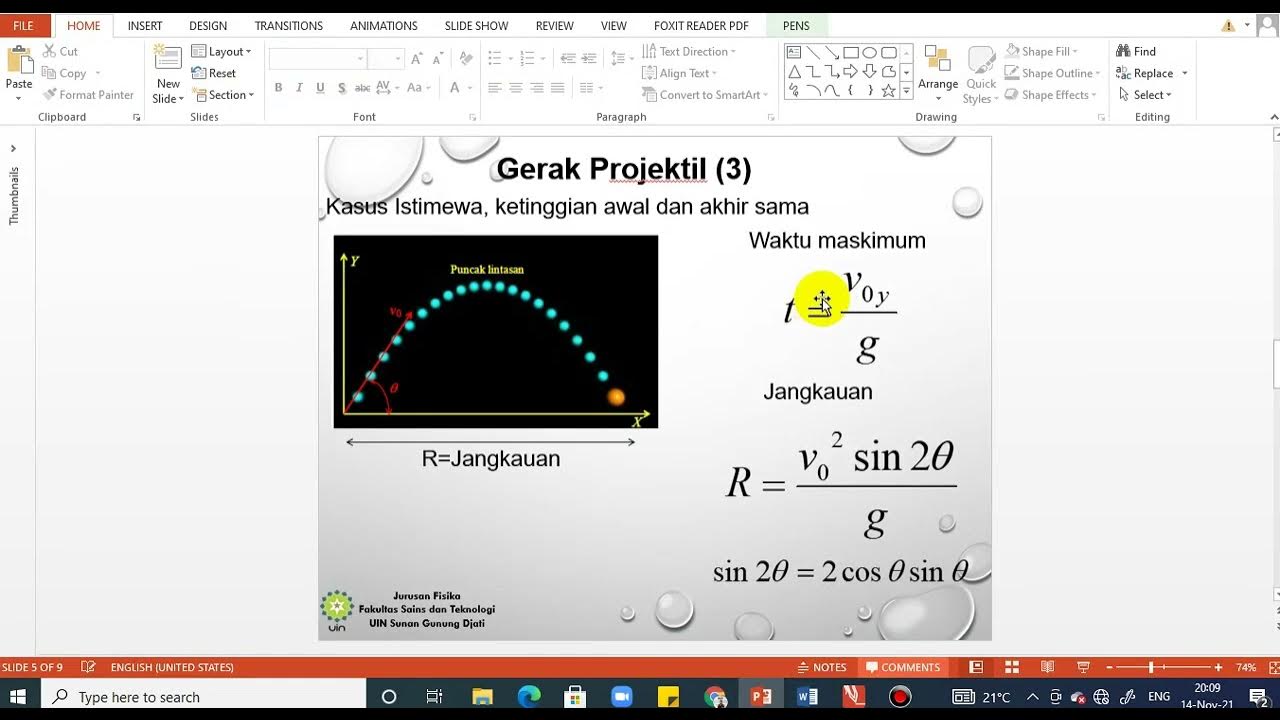
Materi kuliah Fidas IF Gerak 2D

Kinematics Part 1: Horizontal Motion
5.0 / 5 (0 votes)
