Aproximaciones de Riemann rectangulares y trapezoidales

KhanAcademyEspañol

16 Apr 201309:32

Summary

TLDREn este video, se exploran diversas maneras de aproximar el área bajo la gráfica de una función utilizando diferentes métodos. Primero, se utilizan rectángulos con alturas determinadas por la función en los extremos izquierdo y derecho, así como en el punto medio. Luego, se introduce el uso de trapecios, explicando cómo se puede obtener una aproximación más precisa promediando los lados paralelos de los trapecios. Se destaca que estas aproximaciones, aunque variadas, buscan el mismo objetivo: calcular el área bajo una curva, sentando las bases de la integral definida.

Takeaways

📏 En el video, se explica cómo aproximar el área bajo una curva usando rectángulos, comenzando con rectángulos basados en el extremo izquierdo de los intervalos.
📐 La aproximación del área se obtiene sumando las áreas de cada rectángulo, donde el alto es dado por la función evaluada en el extremo izquierdo del intervalo.
🔄 Otra forma de aproximar el área es evaluando la función en el extremo derecho de cada intervalo, lo que cambia las alturas de los rectángulos.
📍 También es posible aproximar el área utilizando el punto medio del intervalo para evaluar la función, creando una mejor aproximación.
🟦 La fórmula básica de la suma de áreas implica la multiplicación de la altura del rectángulo (función evaluada) por el ancho del intervalo (Delta x).
✏️ La longitud del intervalo total es B - A, y Delta x es esta longitud dividida entre el número de rectángulos (n).
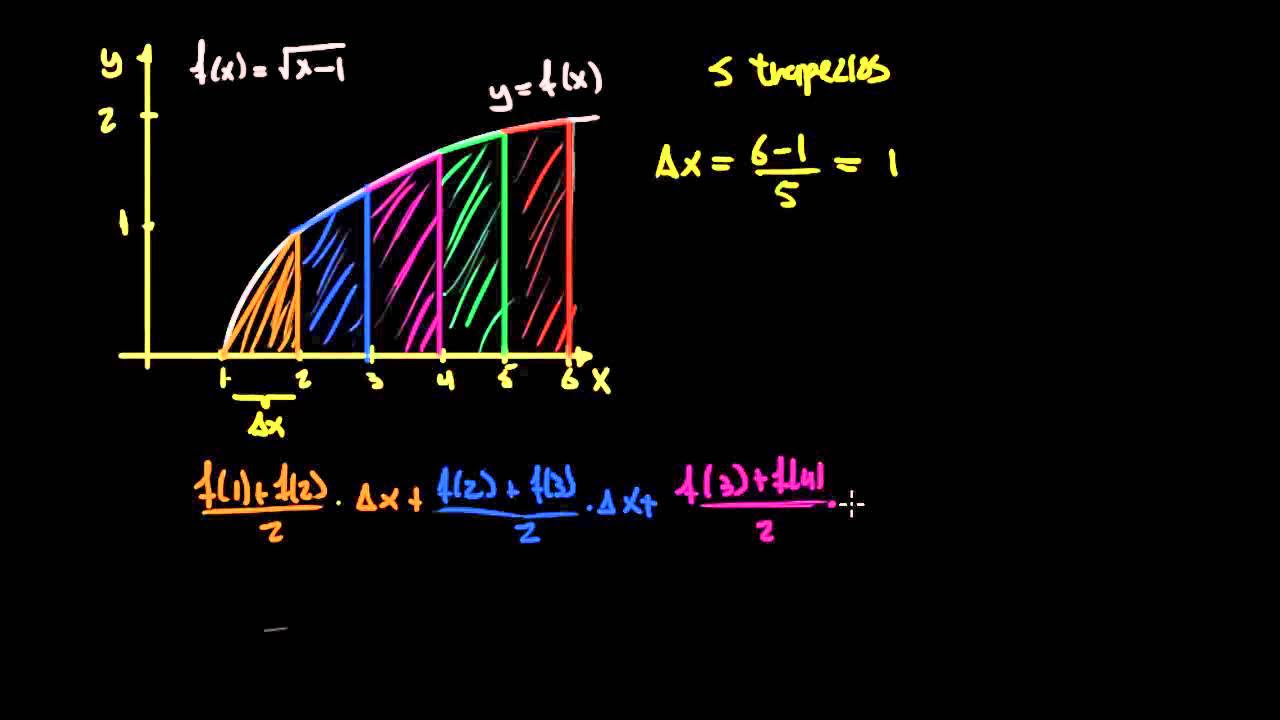
📊 Se describe cómo usar los trapecios en lugar de rectángulos para mejorar la aproximación, promediando las alturas en los extremos del intervalo.
➗ El área de un trapecio se calcula promediando las alturas en los extremos del intervalo y multiplicando por el ancho (Delta x).
📉 Cada método tiene sus propias características y es una forma válida de aproximar el área bajo la curva, utilizando distintas alturas o figuras geométricas.
🧮 Se recuerda que estas aproximaciones son representaciones gráficas de un concepto algebraico más amplio, relacionado con la integral.

Q & A

¿Qué método se usó en los videos anteriores para aproximar áreas bajo la gráfica de una función?
-En los videos anteriores, se usaron rectángulos donde la altura estaba dada por la función evaluada en el extremo izquierdo de cada intervalo.
¿Cómo se calcula el área de un rectángulo en el método de aproximación utilizando extremos izquierdos?
-El área de cada rectángulo se calcula multiplicando la altura, que es F(x) evaluada en el extremo izquierdo del intervalo, por la base, que es Δx, la cual es la longitud del intervalo dividido entre el número de rectángulos.
¿Cómo cambia la aproximación si se evalúa la función en el extremo derecho en lugar del extremo izquierdo?
-Si se evalúa la función en el extremo derecho, los rectángulos tienen alturas dadas por F(x) en el extremo derecho del intervalo, lo que cambia las áreas pero sigue utilizando el mismo Δx para la base.
¿Qué diferencia hay al usar el punto medio para aproximar las áreas?
-Cuando se usa el punto medio, la altura del rectángulo se evalúa en el punto medio entre los dos extremos del intervalo, es decir, F((x0 + x1) / 2), lo que mejora la precisión de la aproximación en algunos casos.
¿Cuál es la fórmula general para aproximar áreas utilizando rectángulos con la altura en el punto medio?
-La fórmula general es la suma de F((xi-1 + xi) / 2) multiplicado por Δx para cada uno de los n rectángulos.
¿Cómo se utiliza el método de los trapecios para aproximar el área bajo una curva?
-El método de los trapecios usa la función evaluada en ambos extremos del intervalo y luego promedia estas alturas para formar un trapecio. El área de cada trapecio se calcula promediando los dos lados paralelos (F(xi-1) y F(xi)) y multiplicando por la base Δx.
¿Cuál es la fórmula para calcular el área de un trapecio en este contexto?
-La fórmula es (F(xi-1) + F(xi)) / 2 multiplicado por Δx.
¿Cómo se determina el valor de Δx en estos métodos de aproximación?
-Δx se calcula como (b - a) / n, donde b y a son los extremos del intervalo y n es el número de subdivisiones o rectángulos/trapecios utilizados en la aproximación.
¿Cuál es la principal ventaja de usar el método del punto medio sobre los extremos izquierdo y derecho?
-El método del punto medio tiende a dar una aproximación más precisa, ya que evalúa la función en un valor central del intervalo, lo que puede compensar las desviaciones que ocurren cuando se usan solo los extremos.
¿Qué aspecto clave se debe recordar sobre los métodos de aproximación discutidos?
-Es importante recordar que estos métodos (extremo izquierdo, extremo derecho, punto medio y trapecios) son formas de aproximar el área bajo una curva, y cada uno ofrece una precisión diferente dependiendo del comportamiento de la función en el intervalo.

Outlines

00:00

📊 Explicación de aproximación de áreas bajo la curva usando rectángulos

En este párrafo, se explica cómo se aproximan áreas bajo la curva de una función utilizando rectángulos. Se menciona que en videos anteriores, los rectángulos se construían evaluando la función en el extremo izquierdo. Se detalla el proceso paso a paso, comenzando con un primer rectángulo, cuya altura está dada por F(x0), y luego avanzando con más rectángulos hasta llegar al enésimo, donde la altura está dada por F(XN-1). La base de los rectángulos es constante y corresponde a Δx, que se calcula como (b-a)/n. La suma de estas áreas genera una aproximación a la integral.

05:00

🔄 Alternativa de aproximación usando el extremo derecho de los rectángulos

Este párrafo introduce una alternativa para la aproximación del área bajo la curva, evaluando la función en el extremo derecho de cada rectángulo en lugar del izquierdo. Aquí, se recalculan las alturas de los rectángulos usando F(x1) para el primero, F(x2) para el segundo, y así sucesivamente hasta F(XN) para el último rectángulo. Se mantiene la misma base (Δx), pero cambia la altura. La suma de las áreas nuevamente produce una aproximación, pero con una diferencia en los valores obtenidos debido a la evaluación en el extremo derecho.

📍 Aproximación con evaluación en el punto medio de los rectángulos

En este párrafo, se propone una tercera forma de aproximar el área bajo la curva, utilizando la función evaluada en el punto medio de cada intervalo en lugar de los extremos. La altura del rectángulo se calcula como F((x0 + x1) / 2) para el primer rectángulo, y se sigue el mismo proceso para los rectángulos subsiguientes. Esta aproximación también involucra multiplicar la altura por la misma base Δx, lo que genera una nueva suma que representa el área bajo la curva con esta técnica de punto medio.

📐 Aproximación usando trapecios

Este párrafo introduce una nueva figura geométrica: el trapecio, para aproximar el área bajo la curva. En lugar de rectángulos, se utilizan trapecios donde un lado es F(xi-1) y el otro es F(xi). La fórmula para el área de un trapecio implica promediar las alturas de los lados paralelos y multiplicar por la base (Δx). Este método es una alternativa más precisa que los rectángulos en algunos casos, ya que tiene en cuenta la pendiente entre los puntos evaluados. La suma de las áreas de los trapecios genera otra forma de aproximar la integral.

Mindmap

Keywords

💡Rectángulo

Un rectángulo es una figura geométrica con cuatro lados rectos y ángulos rectos. En el video, se utiliza esta figura para aproximar el área bajo una curva, donde la altura de cada rectángulo es determinada por el valor de la función en un punto específico. El concepto de rectángulo es clave para entender la primera aproximación del área bajo la gráfica de una función.

💡Delta x

Delta x representa la base de cada rectángulo en la aproximación del área. Es la distancia entre dos puntos sucesivos en el eje x y se obtiene dividiendo la longitud del intervalo entre el número de rectángulos. Es un concepto esencial ya que define el ancho de los rectángulos que se usan para aproximar el área bajo la curva.

💡Función evaluada

Evaluar una función significa calcular el valor de la función para un determinado valor de x. En el video, la función se evalúa en distintos puntos, como en el extremo izquierdo, derecho o el punto medio de cada intervalo. La altura de los rectángulos depende de la función evaluada en estos puntos, lo que afecta la precisión de la aproximación del área.

💡Extremo izquierdo

El extremo izquierdo se refiere al valor más pequeño de x en el intervalo de un rectángulo. En la primera forma de aproximación, la altura de cada rectángulo está determinada por la función evaluada en el extremo izquierdo. Este método ofrece una aproximación específica del área que, dependiendo de la función, puede subestimar o sobrestimar el área real.

💡Extremo derecho

El extremo derecho es el valor más grande de x en el intervalo de un rectángulo. En la segunda aproximación descrita en el video, la altura de los rectángulos está dada por la función evaluada en el extremo derecho. Esto cambia la aproximación del área bajo la curva, en comparación con el uso del extremo izquierdo.

💡Punto medio

El punto medio es el valor de x que está exactamente entre los extremos izquierdo y derecho de un intervalo. En la tercera forma de aproximación presentada en el video, la función se evalúa en este punto medio para determinar la altura de los rectángulos. Este método puede ofrecer una aproximación más precisa que las evaluaciones en los extremos.

💡Trapecio

El trapecio es una figura geométrica con dos lados paralelos. En la cuarta aproximación del área bajo una curva, se utilizan trapecios en lugar de rectángulos. La altura de los lados paralelos del trapecio está dada por los valores de la función en los extremos izquierdo y derecho del intervalo. Esta técnica ofrece una aproximación más cercana al área real que los métodos basados en rectángulos.

💡Área bajo la curva

El área bajo la curva es la cantidad de espacio comprendido entre la gráfica de una función y el eje x. Este concepto es central en el video, ya que las diferentes técnicas mostradas (rectángulos y trapecios) buscan aproximar este área. Es un concepto clave en cálculo integral y es el objetivo de las sumas que se realizan en el video.

💡Suma de Riemann

La suma de Riemann es una técnica matemática para aproximar el área bajo una curva utilizando rectángulos. En el video, se muestran varias versiones de esta técnica, como las sumas de Riemann con el extremo izquierdo, derecho y el punto medio. Es una herramienta fundamental en el cálculo para entender la integral como el límite de estas sumas.

💡Promedio

El promedio se utiliza en el cálculo del área de un trapecio, donde se promedian las alturas de los lados paralelos. Este promedio, multiplicado por la base del trapecio (Delta x), da el área de cada trapecio. En el contexto del video, el promedio permite mejorar la aproximación del área bajo la curva en comparación con el uso de rectángulos.

Highlights

Aproximación de áreas bajo una curva utilizando rectángulos con alturas dadas por la función evaluada en el extremo izquierdo.

La fórmula para la suma de las áreas se realiza desde i = 1 hasta n, considerando la altura de los rectángulos como f(x_i-1) multiplicada por Δx.

La longitud de la base de los rectángulos, Δx, se calcula como (b - a) / n, donde b y a son los límites del intervalo.

Otras formas de aproximar el área incluyen evaluar la función en el extremo derecho, lo que cambia las alturas de los rectángulos.

Evaluación de la función en el punto medio para aproximar el área bajo la curva, utilizando f((x_i-1 + x_i)/2).

Tercer método de aproximación con rectángulos usando la función evaluada en el punto medio de los extremos, una forma más precisa que las anteriores.

Uso de trapecios como otra forma de aproximar el área bajo la curva, considerando los valores de la función en los extremos izquierdo y derecho.

El área de un trapecio se calcula promediando los dos lados paralelos (f(x_i-1) y f(x_i)) y multiplicando por la base Δx.

Resumen de cuatro formas de aproximar áreas bajo una curva: rectángulos por el extremo izquierdo, derecho, punto medio, y usando trapecios.

El primer método usa rectángulos con altura en el extremo izquierdo, resultando en rectángulos ligeramente mayores en algunos casos.

En el método del extremo derecho, la altura de los rectángulos se calcula evaluando la función en x_i, generando rectángulos más pequeños en ciertos intervalos.

Aproximación en el punto medio ofrece una mejor precisión, ya que la función se evalúa en el punto medio entre dos puntos consecutivos.

El uso de trapecios promedia las alturas de los extremos, dando un ajuste más suave entre los puntos y mejorando la aproximación.

Cada uno de estos métodos tiene aplicaciones diferentes, dependiendo del nivel de precisión y la naturaleza de la función que se desea integrar.

Los símbolos matemáticos que representan sumas e integrales en realidad son aproximaciones geométricas que utilizan rectángulos o trapecios.