Calculus - Approximating the instantaneous Rate of Change of a Function

Summary

The video script delves into the concept of instantaneous change in a function, contrasting it with average change by focusing on a single point rather than between two. It illustrates the process of approximating this change by moving a second point closer to the point of interest, observing how the average rate of change converges to a limiting value. This method provides a practical way to estimate the instantaneous rate of change, such as the speed of a rocket or population growth rate, despite its approximation nature. The script teases the introduction of calculus' limits as a more precise tool for future lectures, encouraging viewers to explore further.

Takeaways

• 📈 The concept of instantaneous change in a function is introduced as a way to describe how a function changes at a single point, rather than over an interval.
• 🔍 The distinction between instantaneous and average change is highlighted, with the former focusing on a specific point and the latter considering a range.
• 🚀 Instantaneous change can be applied to real-world situations like the speed of a rocket immediately after launch or the rate of population growth.
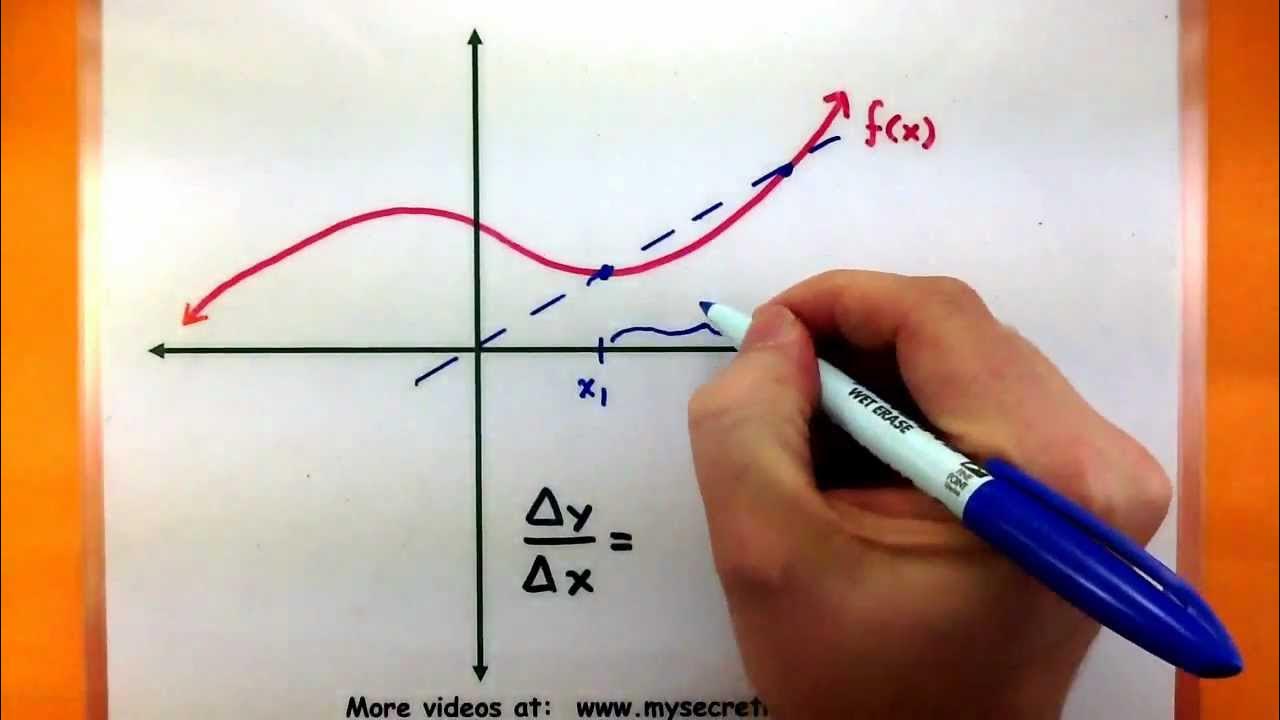
• ❌ The traditional method of finding change using two points results in a 0/0 indeterminate form when trying to apply it to a single point.
• 🔑 The secret to finding change at a single point is to cleverly use the average rate of change and then take a limit as the points converge.
• 📐 The process involves choosing two points, calculating the average rate of change, and then moving the second point closer to the first to observe changes in the rate.
• 📉 As the second point approaches the first, the average rate values converge towards a limiting value, which is an approximation of the instantaneous rate of change.
• 📊 The example provided demonstrates the process of moving a point closer and observing the average rate of change values approach a specific number, indicating a limiting value.
• 🤔 While the limiting value provides a good approximation, it is not exact, and there is a need for a method to determine the exact value the rate is approaching.
• 🧠 Calculus introduces the concept of a limit, which is a tool designed to find the exact value a function approaches, providing a solution to the problem of approximation.
• 📚 The script encourages viewers to look forward to the next lecture on limits and to explore more examples of approximating instantaneous rates of change on the provided website.

Q & A

What is the main concept discussed in the script?

The main concept discussed in the script is the idea of instantaneous change of a function, which is the rate of change at a single point rather than between two points.

Why is it difficult to describe the change of a function at a single point using the usual method?

It is difficult because the usual method requires two points to calculate the change in both the y and x directions. At a single point, it appears there is no change in either direction, leading to a 0/0 indeterminate form when attempting to use the change formula.

What is the alternative method to describe the change at a single point?

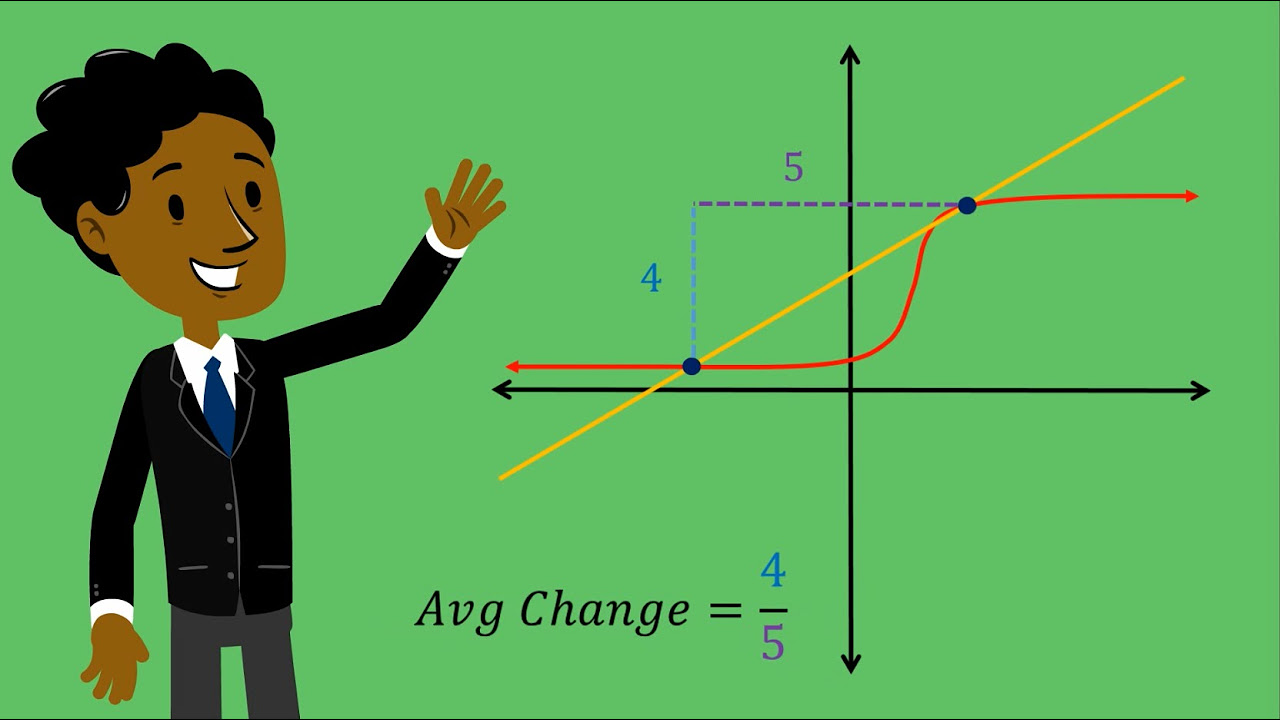
The alternative method is to use the average rate of change between two points and then move the second point closer and closer to the first point, observing how the average rate of change approaches a limiting value.

What is the term used to describe the value that the average rate of change approaches as the second point gets closer to the first point?

The term used is 'limiting value,' which serves as an approximation to the instantaneous change of a function.

Can the limiting value be considered an exact measure of the instantaneous rate of change?

No, the limiting value is an approximation because there is no precise way to determine how close to the limiting value the average rate of change is getting.

What does the script suggest as a more exact method for finding the limiting value?

The script suggests that the concept of 'limit' in Calculus provides a more exact method for finding the limiting value that a function approaches.

What is an example of a real-world application of finding the instantaneous rate of change?

An example given in the script is finding the instantaneous speed of a rocket a few minutes after launch or the instantaneous rate of change of a population.

What is the process of finding the limiting value in the context of the script?

The process involves selecting a point on the function and another point, calculating the average rate of change between them, and then repeatedly moving the second point closer to the first point while recording the new average rate of change until a consistent limiting value is approached.

What is the significance of the number 2 in the example provided in the script?

The number 2 is the limiting value that the average rate of change seems to be approaching as the second point gets closer to the first point, indicating the instantaneous rate of change at that specific point on the function.

How does the script suggest we can improve our understanding of the instantaneous rate of change?

The script suggests that by moving the points closer together and observing the changes in the average rate of change, we can gather more evidence and improve our understanding of the instantaneous rate of change, even without the exact mathematical concept of a limit.