Energía en el Movimiento Armónico Simple. Sistema educativo: FÍSICA INTERACTIVA II
Summary
TLDREn este video, se aborda la energía en sistemas oscilantes como el péndulo simple y el sistema masa-resorte. Se explica cómo la energía mecánica se divide en energía cinética y potencial (gravitatoria y elástica), y cómo se conserva a lo largo del movimiento armónico simple. El análisis incluye la transformación entre energías en ambos sistemas, destacando que la energía mecánica permanece constante debido a la ausencia de fuerzas disipativas. Se presentan las ecuaciones que describen la energía en el sistema masa-resorte y el péndulo, destacando las relaciones entre amplitud, frecuencia angular y masa.
Takeaways
- 😀 El tema principal de la clase es la energía en sistemas oscilantes como el péndulo simple y el sistema masa-resorte.
- 😀 Se estudiará la energía mecánica, que incluye la energía cinética, la energía potencial elástica y gravitatoria.
- 😀 La energía mecánica en un sistema oscilante se mantiene constante debido a la conservación de la energía en ausencia de fuerzas disipativas, como la fricción.
- 😀 En el péndulo simple, la energía potencial gravitatoria se transforma en energía cinética a medida que el péndulo se mueve.
- 😀 En el punto de equilibrio del péndulo, la energía potencial es cero y la energía cinética es máxima.
- 😀 En el sistema masa-resorte, la energía potencial elástica se convierte en energía cinética y viceversa durante el movimiento oscilatorio.
- 😀 La energía potencial máxima en un resorte se alcanza en las posiciones de máxima elongación, mientras que la energía cinética máxima ocurre en el punto de equilibrio.
- 😀 La ecuación de energía mecánica para el sistema masa-resorte se puede expresar como 1/2 * m * ω² * a², donde ω es la frecuencia angular y a la amplitud del movimiento.
- 😀 La energía cinética máxima en el sistema masa-resorte se calcula usando la fórmula 1/2 * m * a² * ω².
- 😀 La energía mecánica en un sistema oscilante depende de las características del resorte y de la masa oscilante, y es independiente de la fricción o calentamiento.
- 😀 La frecuencia angular (ω) en el péndulo depende de la aceleración gravitatoria y la longitud del hilo, lo que influye en la energía mecánica del sistema.
Q & A
¿Qué es la energía mecánica en un sistema oscilante?
-La energía mecánica en un sistema oscilante es la suma de la energía cinética y la energía potencial (gravitatoria y elástica). En los sistemas oscilantes como el péndulo o el sistema masa-resorte, la energía mecánica se conserva durante el movimiento, transformándose entre estas formas sin pérdida de energía.
¿Cómo se comporta la energía en un péndulo simple?
-En un péndulo simple, la energía potencial gravitatoria se convierte en energía cinética conforme el péndulo se mueve. En el punto más bajo (equilibrio), toda la energía es cinética. A medida que el péndulo sube, la energía cinética se convierte en energía potencial, y en el punto más alto la energía cinética es nula mientras la energía potencial es máxima.
¿Qué condiciones ideales se asumen para el estudio del péndulo y el sistema masa-resorte?
-Se asume que no hay fricción en el sistema, que la longitud del hilo del péndulo es mucho mayor que el diámetro de la masa y que las oscilaciones son pequeñas. En el caso del sistema masa-resorte, también se supone que no hay fricción y que el resorte no se calienta durante las oscilaciones.
¿Cuál es la relación entre la energía potencial y la cinética en un sistema masa-resorte?
-En un sistema masa-resorte, la energía potencial elástica y la energía cinética se transforman continuamente entre sí. En los extremos del movimiento, toda la energía es potencial elástica, mientras que en la posición de equilibrio, toda la energía es cinética. La suma de ambas energías es constante a lo largo del movimiento, manteniendo constante la energía mecánica del sistema.
¿Qué factores afectan la energía mecánica en el movimiento de un sistema oscilante?
-La energía mecánica en un sistema oscilante depende de las características del sistema, como la masa del cuerpo, la constante elástica del resorte (en el caso del sistema masa-resorte) y la aceleración de la gravedad (en el caso del péndulo). En condiciones ideales sin fricción, la energía mecánica se mantiene constante.
¿Cómo se puede calcular la energía potencial máxima en un sistema masa-resorte?
-La energía potencial máxima en un sistema masa-resorte se calcula utilizando la fórmula 1/2 * k * a², donde 'k' es la constante elástica del resorte y 'a' es la amplitud del movimiento (máxima elongación del resorte).
¿Qué ocurre con la energía cinética cuando el resorte alcanza su máxima elongación en el sistema masa-resorte?
-Cuando el resorte alcanza su máxima elongación (ya sea positiva o negativa), la energía cinética es nula, ya que la velocidad del cuerpo es cero en esos puntos. Toda la energía del sistema se encuentra en forma de energía potencial elástica.
¿Cómo se relacionan la frecuencia angular y la energía mecánica en un sistema masa-resorte?
-La frecuencia angular (omega) está relacionada con la energía mecánica en un sistema masa-resorte porque la energía potencial máxima en el sistema es igual a 1/2 * m * omega² * a², donde 'm' es la masa, 'omega' es la frecuencia angular y 'a' es la amplitud del movimiento. Esto implica que la energía mecánica depende de la masa y de la constante elástica del resorte.
¿Cómo se calcula la velocidad máxima en un sistema masa-resorte?
-La velocidad máxima en un sistema masa-resorte se calcula usando la fórmula v_max = a * omega, donde 'a' es la amplitud del movimiento y 'omega' es la frecuencia angular. Esta velocidad máxima ocurre en el punto de equilibrio del resorte, donde la energía potencial es mínima y la energía cinética es máxima.
¿Qué sucede con la energía mecánica cuando hay fricción en un sistema oscilante?
-Cuando hay fricción en un sistema oscilante, parte de la energía mecánica se disipa en forma de calor debido a la fuerza disipativa de la fricción. Esto provoca que la energía mecánica total disminuya con el tiempo, lo que resulta en una disminución de la amplitud de las oscilaciones.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Péndulo | Movimiento oscilatorio | Física | Khan Academy en Español

Energía en el movimiento armónico simple
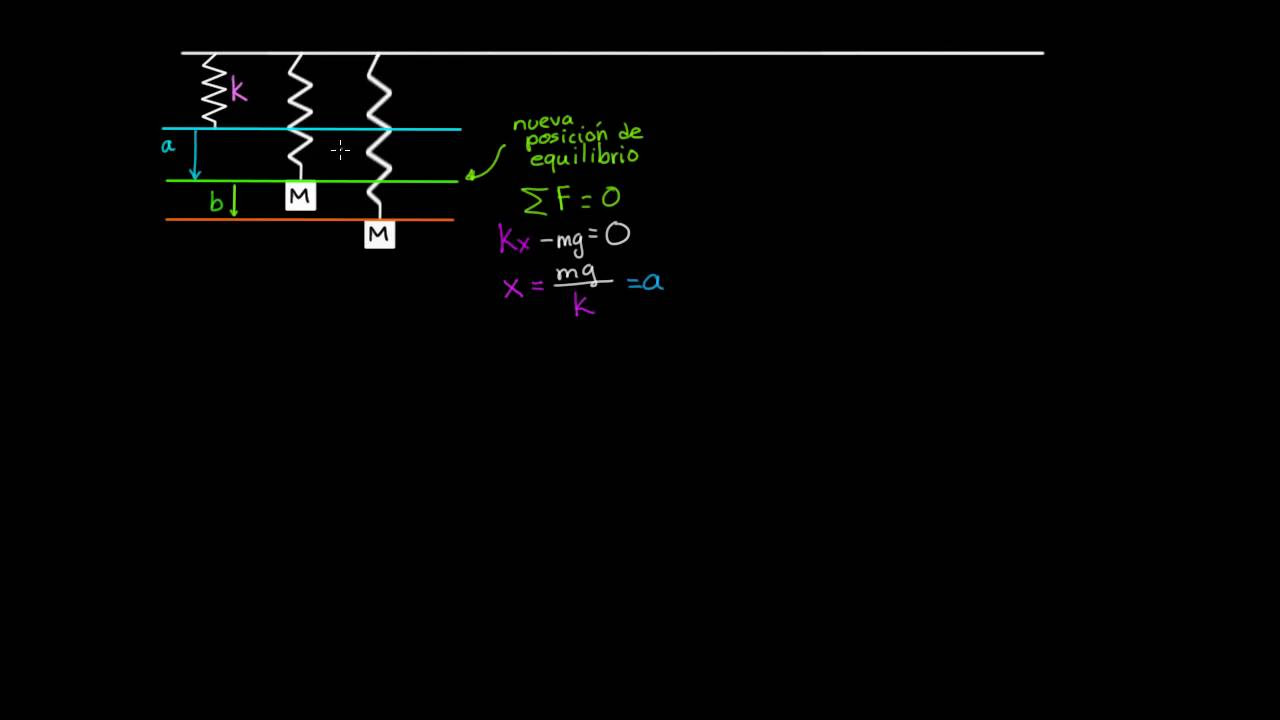
Conservación de la energía y resorte vertical | Física | Khan Academy en Español

Física | Movimiento armónico simple

Aplicaciones del movimiento armónico simple

2025 AP Physics 1 FRQ 2 (Conservation of Mechanical Energy)
5.0 / 5 (0 votes)
